Пример расчета нейтронограммы ядерного рассеяния

Пусть соединение AB имеет объемноцентрированную кубическую решетку, и пусть атомы сорта A занимают углы куба, а атомы сорта B расположены в центре куба:

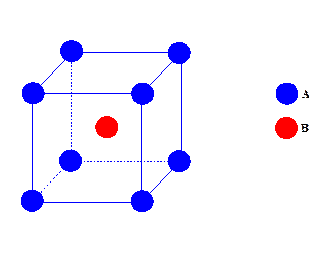
Тогда атом A имеет координаты (0, 0, 0), а атом B - координаты (½, ½, ½). Пусть параметр решетки соединения AB равен a = 4 Ǻ. Примем, что амплитуда когерентного рассеяния атомами сорта A равнаs b _A = 1·10^-12 cm, а атомами сорта B - b _B = -1·10^-12 cm.

Давайте рассчитаем нейтронограмму для этого соединения.

Пусть падающий пучок нейтронов имеет длину волны l = 2 Ǻ, образец представляет собой пластинку, полностью перекрывающую пучок.

Выпишем еще раз формулы для интенсивностей ядерных рефлексов:

I _(hkl) = 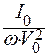l³× j_(hkl) × F ² _(hkl) × LA_(hkl) × T_(hkl) × y ^-1/2× R_(hkl) ×d V, (2.34)

F ²_(hkl) = A ²_(hkl) + B ²_(hkl), (2.35)

A _(hkl) = 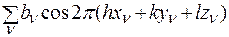, (2.36)

B _(hkl) = 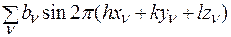. (2.37)

Для простоты рассмотрим случай, когда интенсивность падающего пучка, скорость сканирования и объем образца в пучке постоянны. Будем пренебрегать экстинкцией. Пусть также, атомы A и B не обладают аномально большим поглощением.

Тогда формулу (2.34) можно записать в виде:

I _(hkl) = S · L _(hkl)· j _(hkl)· F ²_(hkl)· T _(hkl) (2.38)

где S масштабный множитель.

В случае кубической структуры следующие рефлексы возможны: (100), (110), (111), (200), (210), и т.д.

Рассчитаем структурные факторы этих рефлексов.

(100)

F ²₁₀₀ = A ²₁₀₀ + B ²₁₀₀

A ₁₀₀ = 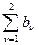·cos2p(1·x_n + 0·y_n + 0·z_n) =

= 1·cos2p(1·1 + 0·0 + 0·0) + (-1)·cos2p(1·½ +0·½ + 0·½) =

= 1·cos2p(0) + (-1)·cos2p(½) = 1·1 + (-1)· (-1) = 2.

A ²₁₀₀ = 2² = 4.

B ²₁₀₀ = 0.

Следовательно, F ²₁₀₀ = A ²₁₀₀ = 4. (2.38)

Рассчитаем структурный фактор F ²₁₀₁ для (101) рефлекса.

A ₁₀₁ = 1·cos2p(1·1 + 0·0 + 1·0) + (-1)·cos2p(1·½ +0·½ + 1·½) =

= 1·1 + (-1)·1 = 0.

B ₁₀₁ = 0.

Итак, F ²₁₀₁ = 0. (2.39)

В случае (111) рефлекса:

A ₁₁₁ = 1·cos2p(1·1 + 1·0 + 1·0) + (-1)·cos2p(1·½ +1·½ + 1·½) =

= 1·cos2p(3) + (-1)·cos2p(1½) = 1·1 + (-1)· (-1) = 2.

A ²₁₁₁ = 4.

B ²₁₁₁ = 0.

F ²₁₁₁ = A ²₁₁₁ = 4. (2.40)

Рассчитаем фактор Лоренца (случай пластинки):

L _hkl = 1/sin²2Q_hkl. (2.41)

Чтобы определить угловые положения рефлексов, воспользуемся формулой Вульфа-Брегга:

sinQ_hkl = l/2 d _hkl, (2.42)

где,

d _hkl = a / 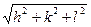, (2.43)

Итак,

sinQ_hkl = l 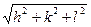/2 a.

Следовательно, угловые позиции рефлексов (100) и (111):

sinQ₁₀₀ = 2 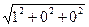/2·4 = ¼, Q₁₀₀ = 14.5°, 2Q₁₀₀ = 29.0° (2.44)

sinQ₁₁₁ = 2 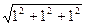/2·4 = √3/4, Q₁₁₁ = 25.6°, 2Q₁₁₁ = 51.2°. (2.45)

Тогда,

L ₁₀₀ = 1/sin²29.0° = 4.255, (2.46)

L ₁₁₁ = 1/ sin²97.2° = 1.016. (2.47)

Рассчитаем фактор повторяемости j _hkl для (100) и (111).

Возможные перестановки для (100):100, -100, 010, 0-10, 001, 00-1.

Следовательно, j ₍₁₀₀₎ = 6.

Возможные перестановки для (111):111, -1-1-1, 1-1-1, -111, 1-11, -11-1, 11-1, -1-11.

Итак, j ₍₁₁₁₎ = 8.

Рассчитаем интенсивности рефлексов (100) и (111).

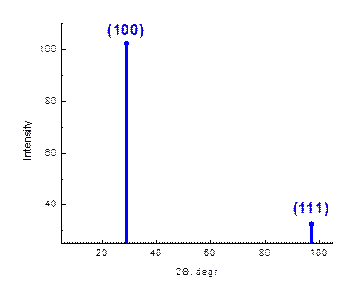
I ₍₁₀₀₎ = 6´4.255´4 = 102.12 (барн), (2.48)

I ₍₁₁₁₎ = 8´1.016´4 = 32.51 (барн). (2.49)

Если не учитывать функцию разрешения дифрактометра, то можно представить наши результаты в виде следующей нейтронограммы соединения. AB.

Рассчитаем поправку на поглощение.

T_hkl = exp (-mt)secQ_hkl (2.50)

Для многокомпонентного образца обычно используют массовый коэффициент поглощения:

m_sample = r_sample[c₁(m₁/r₁) + c₂(m₂/r₂) +...+ c_n(m_n/r_n)], (2.51)

где, m_sample и r_sample – линейный коэффициент поглощения образца и его плотность, c_i - концентрация i-компоненты в образце в массовых %.

Пусть r_sample = 5 g/cm³; m_A/r_A = 2 cm²/g^-1; m_B/r_B = 0.2 cm²/g^-1; c_A = 0.734, c_B= 0.266.

Тогда,

m_sample = 5[(0.734´2) + (0.266´0.2)] = 7.6 (cm^-1).

Пусть толщина образца t = 2 mm = 0.2 cm, тогда поправка на поглощение равна

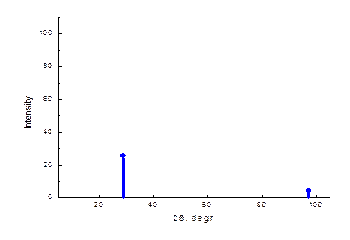
T₁₀₀ = exp(-7.6´0.2´sec14.5°) = exp(-1.57) = 0.25.

T₁₁₁ = exp(-7.6´0.2´sec48.6°) = exp(-2.3) = 0.13.

Как можно видеть, поправка на поглощение достаточно большая. Принимая во внимание поправку на поглощение, уточним вид нашей расчетной нейтронограммы.

Дата добавления: 2014-11-29