Коефіцієнт підсилення

Поглинання і підсилення світла в середовищі.

3.2.1.Закон Ламберта – Бугера - Бера [4] Нехай монохроматичне проміння частоти n поширюється в якомусь середовищі. Для нескінченно тонкого шару середовища dz (див рис.3.1) зміна потоку енергії пропорційна товщині цього шару і інтенсивності падаючого проміння, так що в розрахунку на одиницю площі

(3.1)

де I(n) – спектральна інтенсивність проміння, яке поширюється в напрямку z в розрахунку на одиничний інтервал частот. Повні (або інтегральні) значення густини проміння U, інтенсивності І та інших енергетичних характеристик визначаються інтегруванням по всьому інтервалу частот:

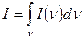і т.д.

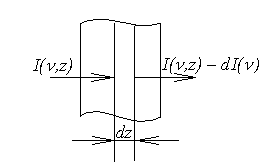
Рис.3-1.При проходженні середовища товщиною dz інтенсивність світлового пучка змінюється.

Пропорційність dI(n)~dz встановлена Ламбертом. Бугер відмітив незалежність відношення від інтенсивності. Закон Ламберта - Бугера, встановлений рівнянням (3.1), характеризує область так званої лінійної оптики, коли величина k(n) не залежить від інтенсивності випромінювання. Коефіцієнт пропорційності k(n) – називають коефіцієнтом поглинання або коефіцієнтом підсилення, в залежності від того інтенсивність зменшується чи зростає при поширенні світлового пучка в середовищі. Інколи величину k( n) називають показником поглинання чи підсилення, що більш правильно. Щоб врахувати зміну інтенсивності світлового пучка від шляху проходження його в середовищі далі записуватимемо її у вигляді I(n,z).

Незалежність відношення , а отже і k(n) від інтенсивності дозволяє нам проінтегрувати диференційне рівняння (3.1):

,

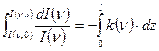де l - довжина середовища, в якому поширюється світловий пучок.

Інтегрування дає такий вираз:

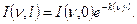, (3.1¹)

що є інтегральним законом Ламберта - Бугера. Він справедливий лише за умови незалежності k(n) від інтенсивності, тобто коли внеском вимушених переходів у зміну інтенсивності можна знехтувати. Закон Ламберта – Бугера встановлений рівнянням (3.1¹), характеризує область так званої лінійної оптики, коли величина k(n) не залежить від інтенсивності проміння. Диференційне рівняння (3.1) справедливе за будь-яких умов.

3.2.2. Потужність поглинання, коефіцієнти поглинання і підсилення. З іншого боку, розглядаючи кількість переходів між двома атомними рівнями 1 і 2 (при цьому зауважимо, що рівень 2 завжди є збудженим, а рівень 1 може бути як найнижчим, основним, так і збудженим, але енергія збудження у нього менша ніж у рівня 2), зміна інтенсивності світлового пучка dI(n) в шарі товщиною dz і його поперечного перерізу в одиницю площі дорівнює різниці фотонів, поглинутих в об’ємі s×dz=1×dz в розрахунку на одиничний інтервал частот – b₁₂(n)×N₁×U(n)×dz, і випромінюваних в тих же умовах b₂₁(n)×N₂×U×(n)×dz, помноженій на енергію фотона hn. Отже,

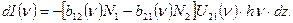(3.2)

Враховуючи, що інтенсивність світлового пучка рівна густині електромагнітної енергії U(n) помноженій на швидкість поширення світла в даному середовищі u

I(n)=u×U(n), (3.3) _

рівняння (3.2) перепишеться так:

(3.4)

де 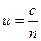- швидкість світла в середовищі, c - швидкість світла у вакуумі, n - показник заломлення середовища. Порівнюючи останнє співвідношення(3.4) із (3.1) маємо

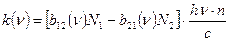(3.5)

Використовуючи (2.7), одержимо:

(3.6)

Якщо N₂ << 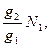то k_n ~N₁ - коефіцієнт поглинання прямо пропорційний концентрації поглинаючих атомів, що є математичним виразом закону Бера, який встановив, що коефіцієнт поглинання пропорційний концентрації поглинаючих атомів N₁.

Отже, результат взаємодії проміння із середовищем – поглинання світла чи його випромінювання, буде залежати від знаку виразу в дужках у співвідношенні (3.6), тобто від заселеності рівнів 1 і 2. В стані термодинамічної рівноваги, коли заселеність рівнів визначається ф-лою Больцмана (2.5) співвідношення (3.6) буде мати вигляд:

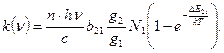(3.7)

При збільшенні температури середовища в будь-яких межах завжди 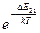<1. Отже, за будь –якої температури 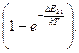>0, а тому k(n)>0 і в цих умовах маємо поглинання світла.

Для підсилення світла необхідно, щоб у (3.6)

N₂ > 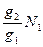(3.8)

Такий стан називається інверсією населеності, тобто коли на верхньому рівні концентрація атомів більша ніж нижньому, що є зворотнім (інверсним) розподілу Больцмана. Зрозуміло, що при інверсії населеності термодинамічна рівновага відсутня і розподіл атомів по енергетичних рівнях закон Больцмана не описує. З врахуванням (3.6), (3.8) і (2.11)

(3.9)

буде коефіцієнтом підсилення. Підставивши це значення в інтегральний закон Ламберта – Бугера – Бера (закон ЛББ), бачимо, що інтенсивність світлового пучка при поширенні в середовищі, в якому N₂> 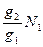, зростає. Отже, це є необхідною умовою виникнення лазерного випромінювання.

При порівнянні виразу (3.9) із рівнянням (3.6), видно, що в законі ЛББ коефіцієнт поглинання позитивний, а коефіцієнт підсилення негативний. В подальшому, щоб уникнути непорозумінь, при аналітичному описі підсилення світла закон ЛББ будемо записувати так:

,

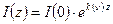вважаючи, що коефіцієнт підсилення k(n) - позитивний.

Дата добавления: 2014-11-29