Незалежність криволінійного інтегралу від шляху інтегрування

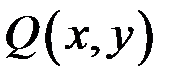Теорема 10.2. Нехай і неперервні функції разом зі своїми частинними похідними 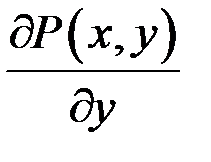і 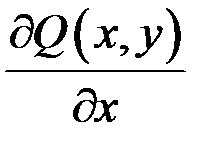у плоскій однозв’язній області 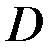. Тоді кожне з чотирьох тверджень:

1) для довільного кусково-гладкого замкненого контуру

, (10.2)

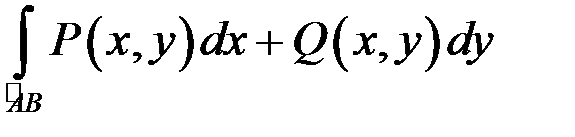2) для довільних точок значення інтеграла (10.3)

не залежить від кривої , яка з’єднує ці точки (незалежність від шляху),

3) вираз є повним диференціалом деякої функції в області , тобто існує така функція 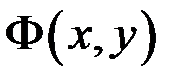, визначена в , що 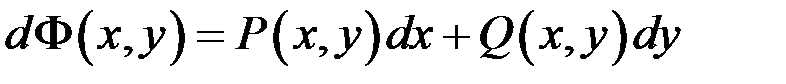, (10.4)

4) для довільної точки 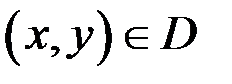: , (10.5)

має наслідком три останніх.

1)

3)

5)

6)

Доведення. Доведення будемо проводити за такою схемою:

2)

4)

Рис. 10.11

I. j     k Нехай виконується умова (10.2). Доведемо, що інтеграл не залежить від шляху інтегрування. Виберемо довільно точки 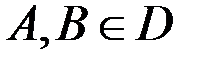і 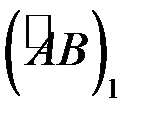, 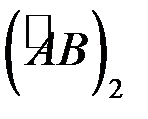- дві довільні кусково гладкі криві з . Об’єднання цих кривих 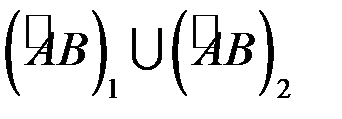утворює замкнену кусково-гладку криву (рис.10.11). Згідно з умовою 1) теореми криволінійний інтеграл вздовж довільної замкненої кривої дорівнює нулю, а використовуючи властивість адитивності криволінійного інтеграла другого роду, отримаємо: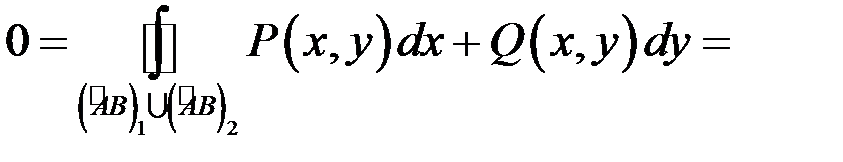

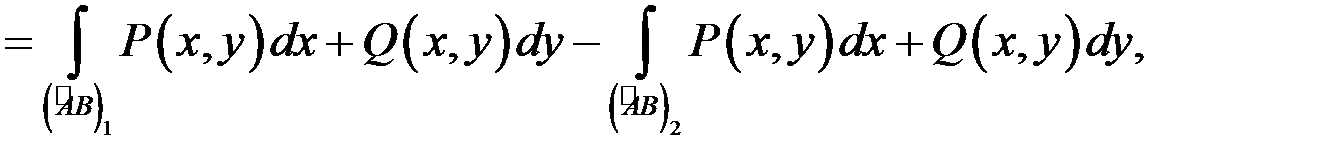
звідки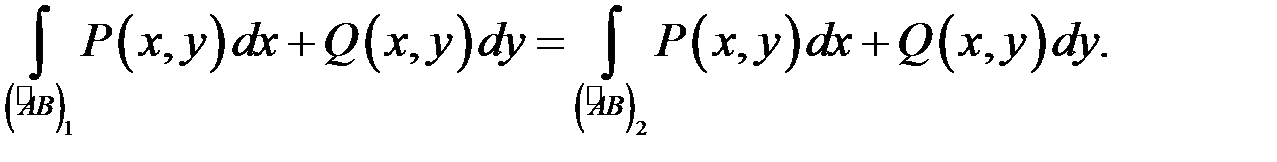

А це й означає, що 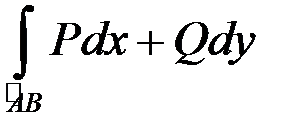не залежить від шляху . ■

ІІ. k    l Нехай інтеграл (10.3) не залежить від шляху інтегрування. Доведемо, що диференціальний вираз інтеграл є повним диференціалом деякої функції двох змінних.

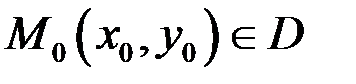Зафіксуємо деяку точку , і візьмемо довільну точку 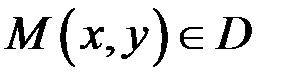. Сполучимо їх кусково-гладкою кривою (рис.10.12). Оскільки інтеграл (10.3) не залежить від шляху інтегрування, то інтеграл є функцією від точки :

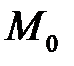
Рис. 10.12

Покажемо, що для довільної точки

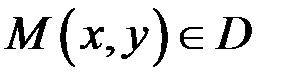
(10.6)

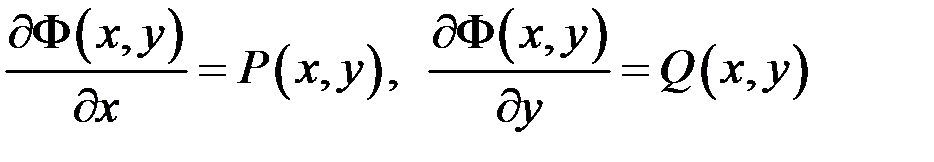
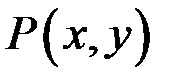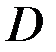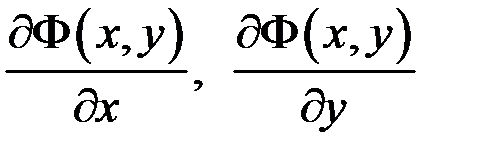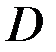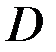Дійсно, оскільки функції і неперервні в області , то і функції були б неперервними в , і звідси випливало б, що функція диференційовна в (див. відому теорему), причому

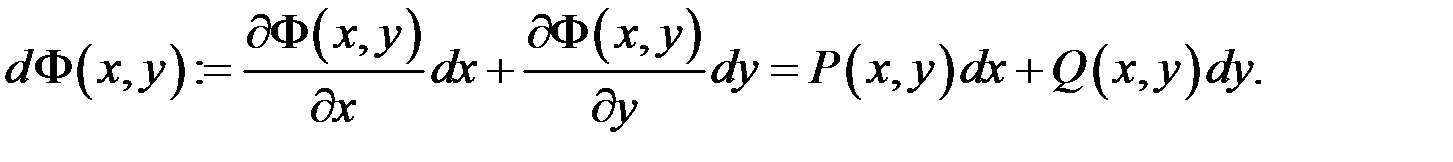
Зафіксуємо тепер точку і візьмемо точку 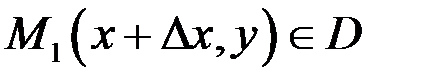. При достатньо малому 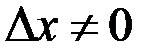відрізок . Тоді

Відрізок , отже

(тут ми використали теорему про середнє для визначеного інтеграла від неперервної функції). Розділимо ліву і праву частину останньої рівності на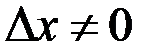

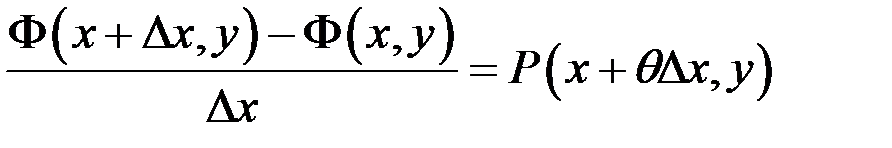
і перейдемо до границі при :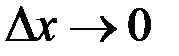

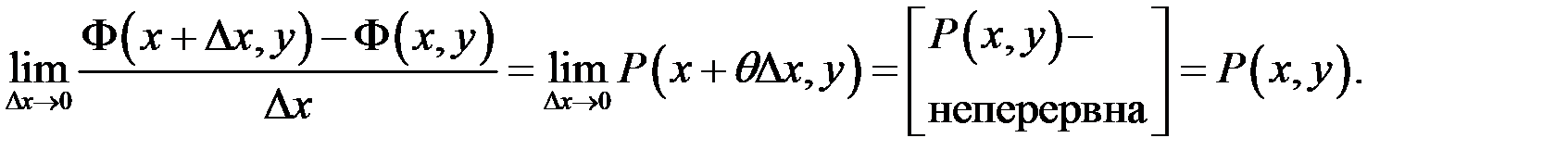
Отже 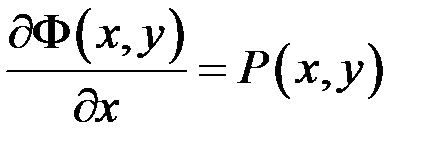. Аналогічно доводиться, що ■

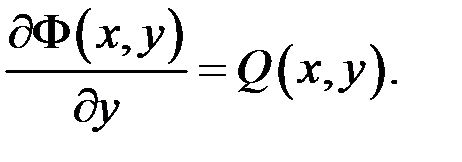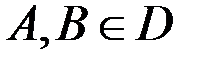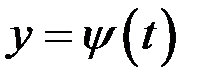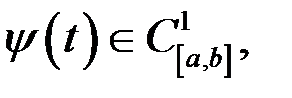
Бачимо, що якщо взяти дві довільні точки і кусково-гладку криву , яка визначається рівняннями , 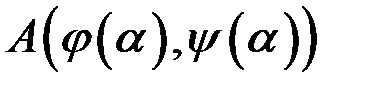- початкова, - кінцева точки кривої 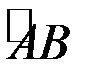, то використавши формулу (9.3) обчислення криволінійного інтегралу другого роду, отримаємо

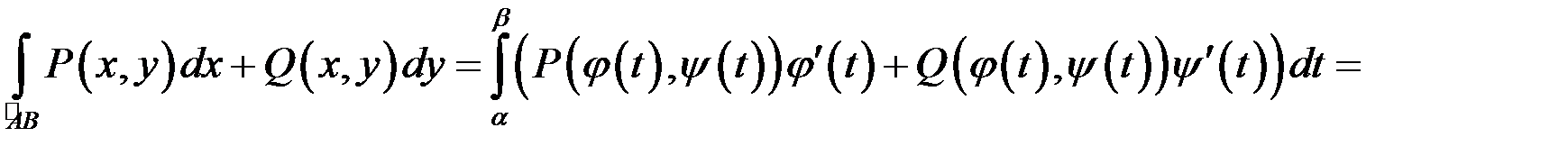
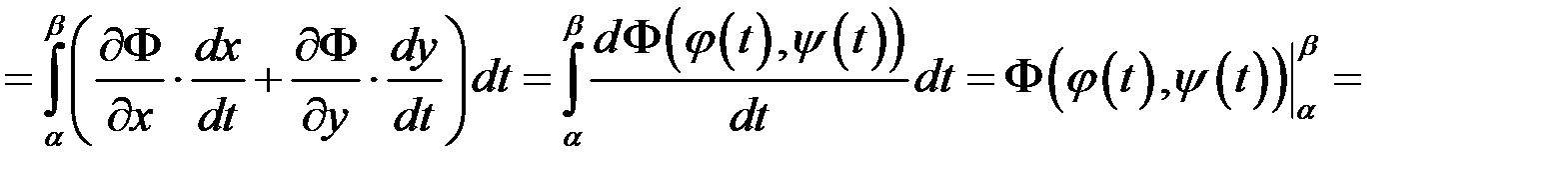
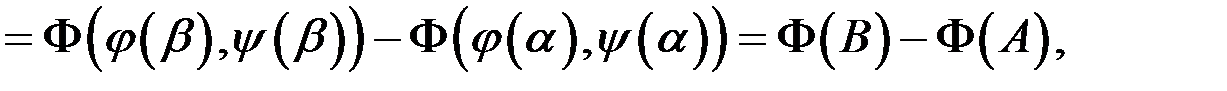
або

(10.7)

ІІІ. l    j Нехай виконується умова (10.4): 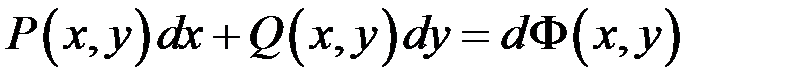. Доведемо, що криволінійний інтеграл вздовж довільної замкненої кусково-гладкої замкненої кривої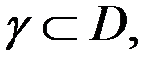 , дорівнює нулеві. Дійсно,

■

IV. l    m Якщо виконується умова (10.4), то

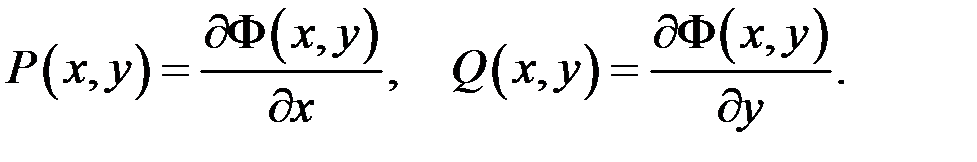
Продиференціюємо першу рівність по змінній 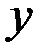, а другу – по змінній , отримаємо:

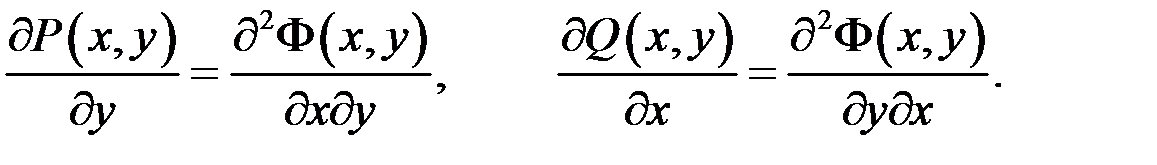
Оскільки змішані похідні рівні між собою: , то й , отже виконується умова 4) теореми. ■

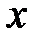
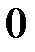
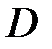
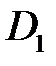
Рис. 10.13

V. m      j Нехай . Доведемо, що криволінійний інтеграл вздовж довільної кусково-гладкої замкненої кривої з цієї області дорівнює нулеві (рис.10.13). Дійсно, за формулою Гріна маємо:

,

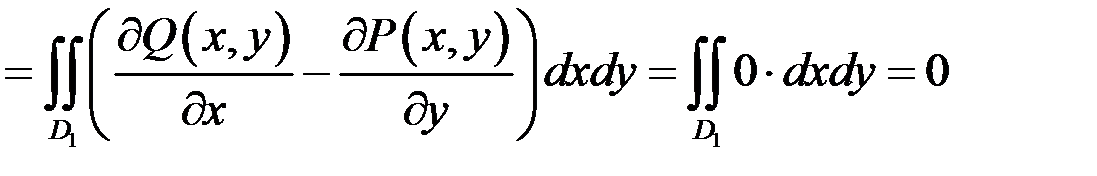що й треба було довести. ■

(10.6)

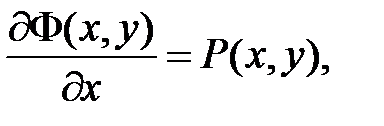
Рис. 10.14

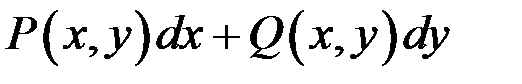VI. m     l Нехай виконується умова (10.5). Покажемо, що в цьому випадку вираз є повним диференціалом деякої функції двох змінних, тобто знайдеться функція 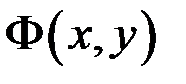, визначена в , така, що правильні рівності (10.6):

Розглянемо в області деякий прямокутник (рис.10.14). Побудуємо функцію 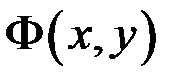наступним чином. Візьмемо і зафіксуємо 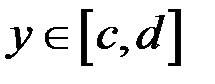. Проінтегруємо першу рівність з (10.6):

,

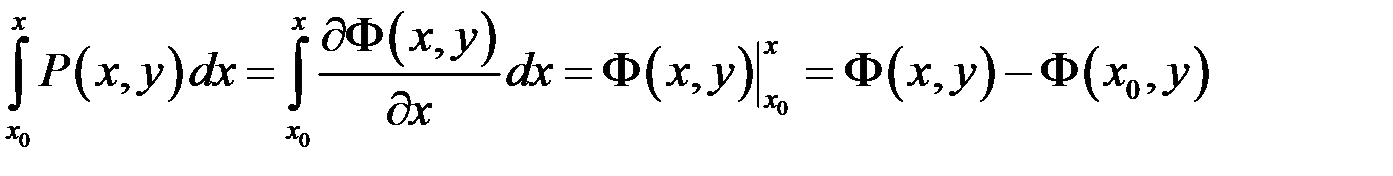звідки .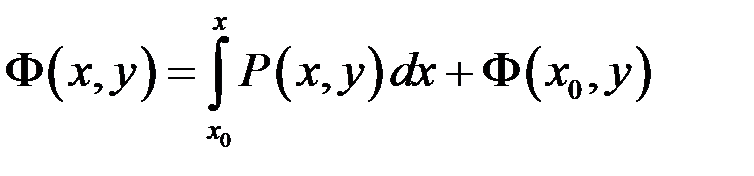

У другій рівності з (10.6) покладемо і проінтегруємо її по :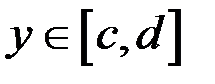

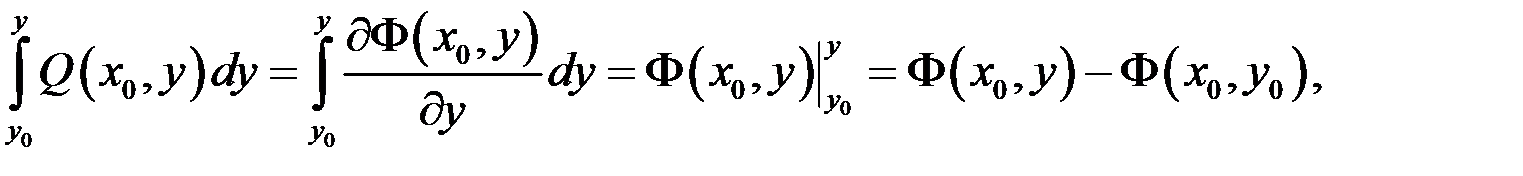звідки , тоді

. (10.8)

Покажемо, що побудована функція задовольняє умови (10.6) . З цією метою обчислимо частинні похідні від функції (10.8) по змінних і :

Таким чином, ми побудували функцію таку, що . ■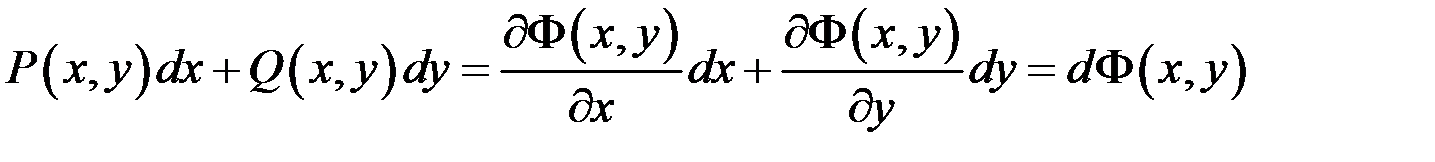

Приклад 1. Обчислити криволінійний інтеграл

.

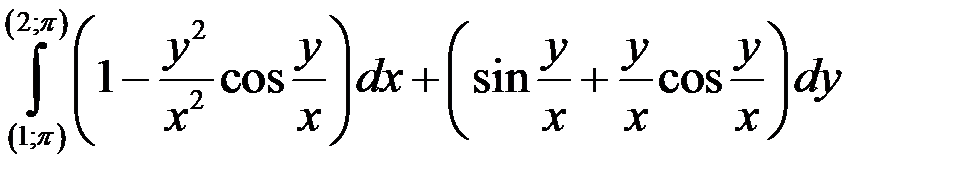Розв’язання. Спочатку переконаємося, що інтеграл не залежить від шляху інтегрування. З цією метою знайдемо частинні похідні відповідно по змінних 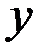і 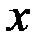від функцій , :

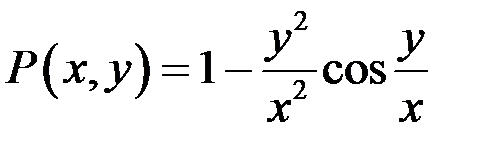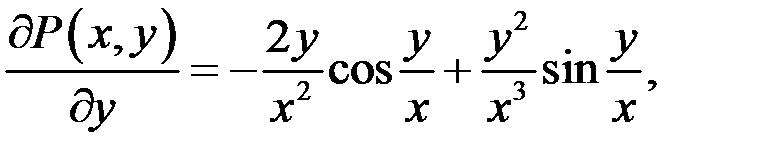
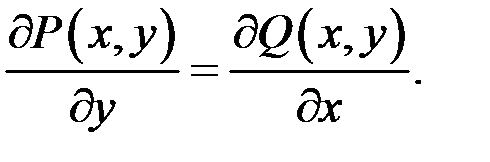
Тому інтеграл можна обчислити вздовж довільної кривої, що з’єднує точки 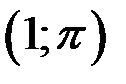, , зокрема відрізка прямої, рівняння якої .

■

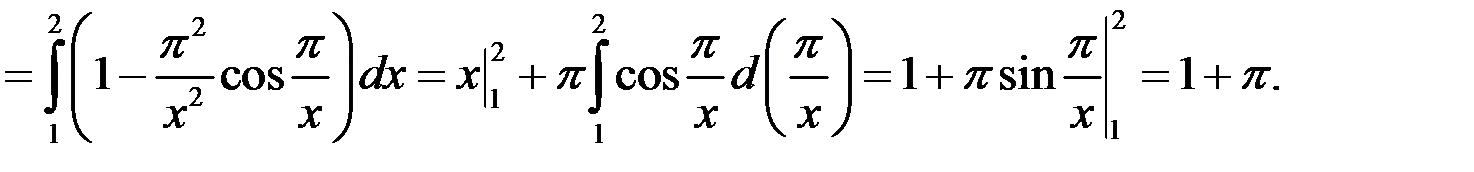Приклад 2. Перевірити, чи є вираз

повним диференціалом функції двох змінних, і якщо так, то знайти цю функцію.

Розв’язання. І спосіб. Знайдемо частинні похідні відповідно по змінних 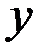і 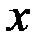від функцій , :

, ,

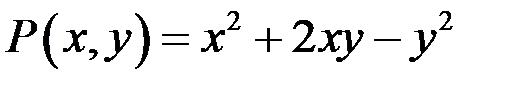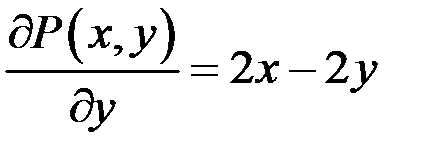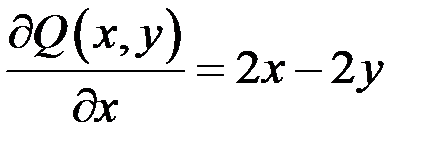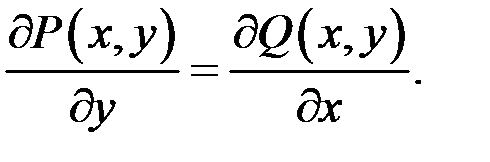
Отже, даний вираз є повним диференціалом від функції двох змінних, тобто 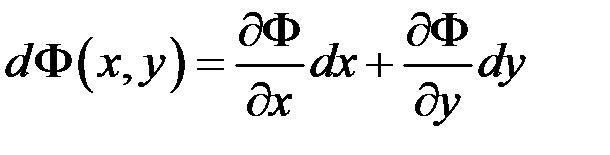, а

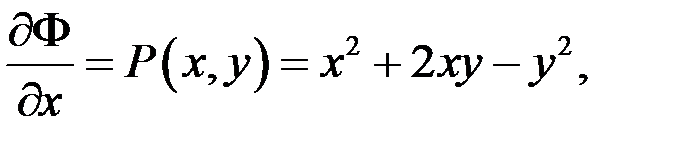
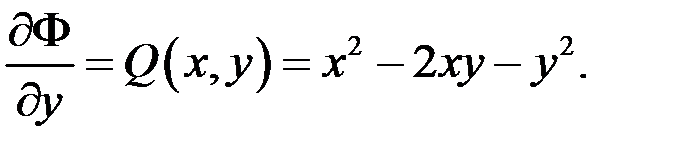(10.9)

З першої рівності (10.9), після інтегрування по змінній , отримаємо:

Невідому функцію 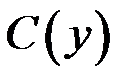знайдемо, скориставшись другою рівністю з (10.8):

,

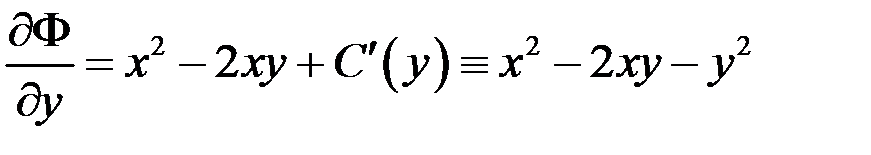або

Отже ■

ІІ спосіб. Використаємо формулу (10.8).

■

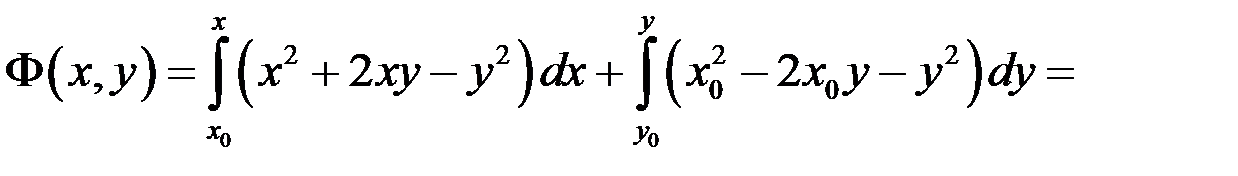
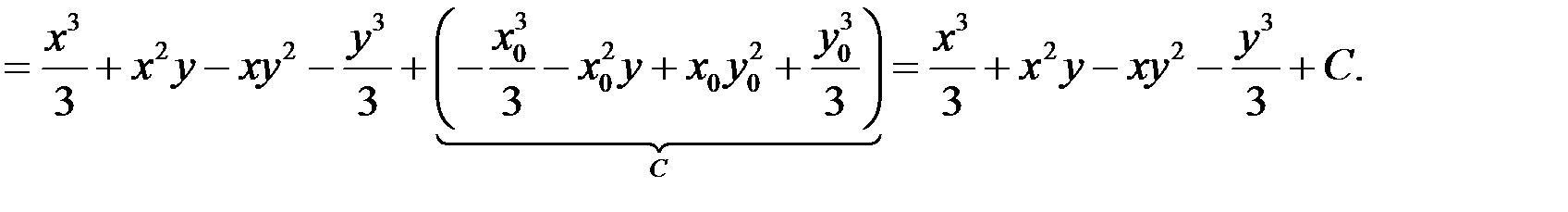Приклад 3. Обчислити за допомогою формули Гріна–Остроградського криволінійний інтеграл 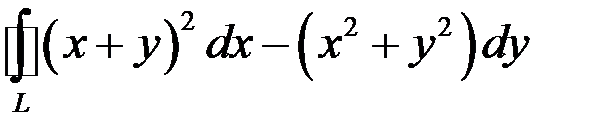, де – контур трикутника з вершинами , , 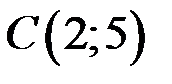у додатному напрямку.

Розв’язання. Знайдемо спочатку рівняння прямих , і (рис.10.15):

.

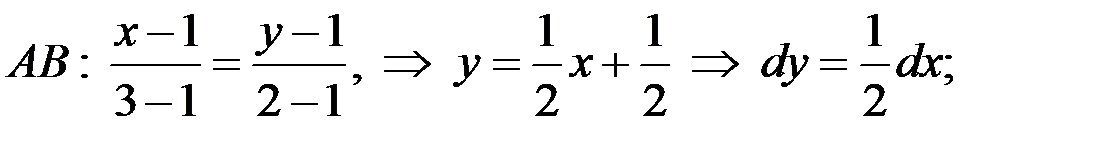
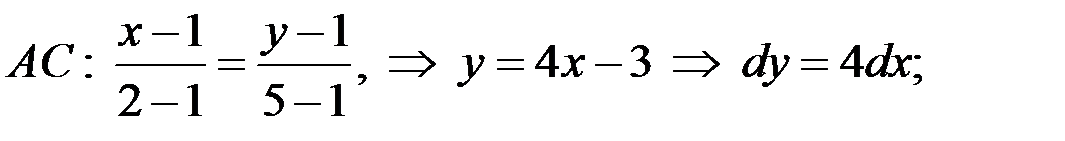
Тепер знайдемо частинні похідні відповідно по змінних 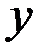і 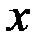від функцій , : , 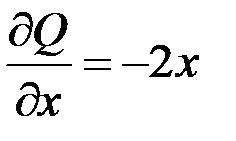. Отже, за формулою Гріна–Остроградського маємо:

■

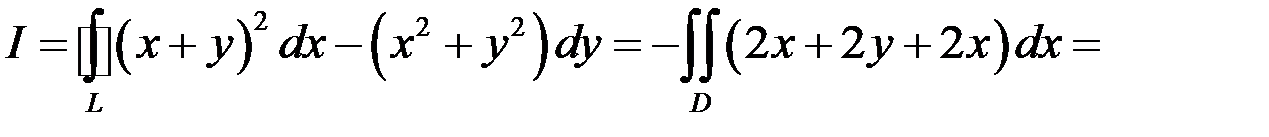
Дата добавления: 2014-11-29