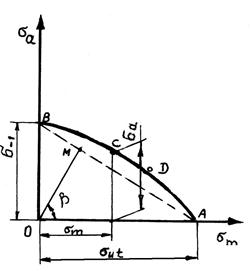
Влияние коэффициента асимметрии цикла на усталостную прочность. Диаграмма предельных циклов напряжений

Наиболее просто экспериментально определить предел выносливости материала σ_–1 при симметричном цикле нагружения. Испытания показали, что коэффициент асимметрии R цикла влияет на величину предела выносливости. Минимальное значение σ_R имеем при симметричном цикле (σ_–1) и максимальное – при отнулевом (σ₀). При расчетах на усталостную прочность желательно знать значения предела выносливости материала при разных величинах коэффициента асимметрии цикла. Это можно определить с помощью диаграмм предельных циклов напряжений. Предельными называют циклы напряжений, наибольшее напряжение которых равно пределу выносливости, т.е. σ_max = σ_R. Из определения характеристик цикла видно, что наибольшее напряжение цикла равно сумме среднего напряжения σ_m (σ_m = (σ_max + σ_min)/2) и амплитуды цикла σ_a (σ_a = (σ_max – σ_min)/2), т.е.

σ_max = σ_m + σ_a. (5.103)

Рис. 5.35

Диаграмму предельных циклов напряжений строят в координатах σ_m – σ_a (рис. 5.35). Точка А диаграммы соответствует пределу прочности материала σ_ut при статическом растяжении, точка В – пределу выносливости σ_–1 при симметричном цикле. Промежуточные точки диаграммы можно определить, используя зависимость (5.103) при обработке результатов испытаний на оборудовании, позволяющем создавать асимметричные циклы нагружения. Например, задавшись средним напряжением σ_m, устанавливаем в результате серии испытаний значение предельной амплитуды σ_a, соответствующей базовому числу циклов нагружения. Результат представляют на диаграмме точкой С. Продолжая испытания с разными величинами σ_m, получают множество точек, через которые должна проходить кривая искомой диаграммы. Площадь диаграммы, ограниченная кривой АDСВ и осями координат, определяет область безопасных с точки зрения разрушения циклов нагружения. Полученная путем сложных длительных испытаний кривая может быть заменена прямой АВ. Рабочая область безопасного нагружения сократится, но при этом получаем погрешность, увеличивающую запас прочности рассчитываемых элементов. Упрощенную диаграмму легко построить, для этого достаточно знать только значения предела прочности материала при растяжении σ_ut и предела выносливости σ_–1 при симметричном цикле нагружения. Имея приближенную диаграмму предельных циклов напряжений (см. рис. 5.35), можно определить предел выносливости σ_R при любом цикле нагружения. Если известен коэффициент асимметрии R цикла нагружений, величину σ_R определяют по диаграмме в следующей последовательности.

Произвольный луч ОМ диаграммы является геометрическим местом точек, характеризующих циклы с одинаковым коэффициентом асимметрии R. Угол наклона β луча к оси σ_m связан с величиной R следующей зависимостью:

tg β = σ_a/σ_m = (1 – R)/(1+R). (5.104)

Для определения по диаграмме искомого предела выносливости при известном R проводим под углом β = arctg [(1 – R)/(1 + R)] к оси абсцисс луч из точки О до пересечения в точке М с прямой АВ. Предел выносливости σ_R находим, используя выражение (5.103) как сумму координат точки М (σ_R = = σ_m + σ_a).

Для отнулевого цикла можно принять σ₀ ≈ (1,45 … 1,65)σ_–1.

Дата добавления: 2014-11-29