Винтовые пружины

Назначение, классификация, основные свойства и материалы упругих элементов

Деформации деталей механизмов нежелательны, так как изменение размеров ведет к появлению дополнительных зазоров, натягов, погрешностей взаиморасположения в соединениях; уменьшает точность передачи; увеличивает потери на преодоление сил трения. Но существует большая группа деталей, основным рабочим свойством которых является значительная упругая деформация, полезно используемая для различных целей, их называют упругими элементами (УЭ).

Упругие элементы делятся на стержневые и оболочковые. К стержневым УЭ относятся винтовые пружины растяжения (рис. 10.1, а) и сжатия (рис. 10.1, б), проволока которых при деформации пружины скручивается; винтовые пружины кручения (рис. 10.1, г) и плоские пружины (рис. 10.1, в, д), материал которых испытывает деформацию изгиба. Материал оболочковых упругих элементов испытывает сложную деформацию, к таким элементам относят: гофрированные трубки–сильфоны (рис. 10.1, е); плоские и гофрированные мембраны (рис. 10.1, ж); мембранные коробки (рис. 10.1, з); трубчатые пружины (рис. 10.1, и).

По назначению упругие элементы делятся на силовые, измерительные и элементы упругих связей. Силовые УЭ применяются для силового замыкания кинематических пар – прижима звеньев в фрикционных, кулачковых и храповых передачах, муфтах; для накопления механической энергии, необходимой для возврата в исходное положение или приведения в движение (пружинные двигатели) подвижных звеньев механизмов. Измерительные УЭ используются в манометрах, динамометрах, термометрах и электроизмерительных приборах как чувствительные элементы устройств для измерения давлений, сил и моментов сил, температур и других параметров. Часто функцию измерительного элемента совмещают с функцией токопровода. Тонкие винтовые и спиральные пружины применяют как токоведущие упругие элементы. Элементы упругих связей используют при замене жесткой связи деталей упругой (упругие муфты, подразд. 12.2), как резиновые и пружинные амортизаторы (рис. 10.1, к) для виброизоляции устройств и поглощения энергии удара.

к

и

Рис. 10.1

з

ж

е

д

г

в

б

а

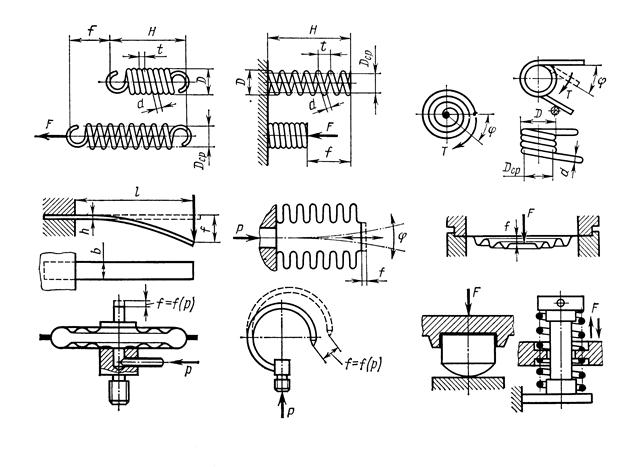
По виду деформации упругие элементы делятся на элементы, испытывающие кручение, изгиб и сложную деформацию.

Эксплуатационные свойства упругих элементов связаны с их упругой характеристикой – зависимостью между деформацией (линейной f или угловой j) и вызывающей ее нагрузкой (соответственно силой F, давлением P, моментом Т). Характеристика упругого элемента (рис. 10.2, а) в зависимости от его конструкции и упругих свойств может быть линейной (кривая 1) – наиболее предпочтительной, нелинейной – возрастающей (кривая 3) и затухающей (кривая 2). Обычно упругая характеристика ограничивается предельной нагрузкой F_пр и соответствующей ей предельной деформацией (удлинение, осадка и т.д.), при которой появляются заметные остаточные деформации или начинается разрушение.

Максимальную деформацию или максимальную нагрузку, которые не должны превышать допускаемых значений, обычно задают из условий эксплуатации, т.е.

f_max £ f_adm или F_max £ F_adm. (10.1)

б

Рис. 10.2

а

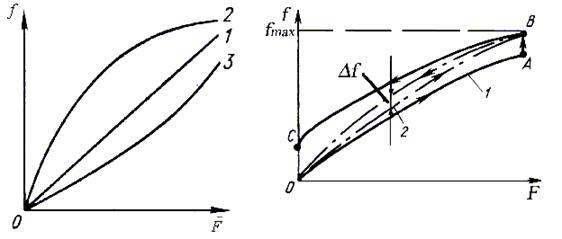
Упругая характеристика наиболее часто представляется в графической форме, реже – в аналитической. При использовании упругих элементов с линейной характеристикой упрощаются их расчеты, конструкции, регулировка.

Силовое противодействие элемента упругой деформации, его упругость характеризуются жесткостью. Жесткость – это нагрузка, при действии которой упругий элемент получает единичную деформацию. Она является важнейшей характеристикой силовых упругих элементов. Для УЭ с линейной упругой характеристикой жесткость k постоянна и равна

k = F / f; k = P / f или k = Т / j. (10.2)

Для измерительных упругих элементов удобнее пользоваться понятием чувствительности (податливости). Чувствительность оценивают деформацией (перемещением), которую получит упругий элемент при действии единичной нагрузки. Чувствительность d – величина, обратная жесткости:

d = 1 / k. (10.3)

При использовании УЭ с нелинейной упругой характеристикой жесткость элементов оценивают как производную от нагрузки по деформации и соответственно – чувствительность, т.е.

k = dF / df; d = df / dF. (10.4)

В конструкциях иногда приходится применять несколько совместно работающих упругих элементов (винтовых пружин). Их суммарные характеристики зависят от схемы соединения упругих элементов. При параллельном соединении УЭ суммарная жесткость упругой системы равна сумме жесткостей ее составляющих. При последовательном соединении упругих элементов каждый элемент деформируется пропорционально его чувствительности, а суммарная чувствительность системы равна сумме чувствительностей всех упругих элементов, входящих в систему.

Жесткость и чувствительность характеризуют одно и то же свойство упругого элемента – способность деформироваться при действии внешней нагрузки.

Влиять на упругую характеристику могут температура, вибрации и другие условия эксплуатации. К погрешностям, проявляющимся особенно в измерительных устройствах, приводят несовершенные упругие свойства материала, вызывающие упругое последействие и упругий гистерезис. Упругое последействие проявляется в запаздывании деформации элемента по сравнению с изменением прилагаемой нагрузки. На упругой характеристике (рис. 10.2, б) это явление отмечено участками АВ и СО кривой 1.

Упругий гистерезис проявляется в несовпадении характеристик элемента при нагружении и снятии нагрузки (см. рис. 10.2, б, кривая 2). Величина гистерезиса Df зависит от напряжений в материале элемента. Поэтому для измерительных элементов допускаемые напряжения связывают не с прочностными характеристиками материала, а с допустимым значением гистерезиса, значение которого не выходит за пределы 0,5... 1,5% от величины f_max, т.е. (Df / f_max)100 £ (0,5 … 1,5).

Неизменность, стабильность упругих характеристик элементов достигается правильным выбором материала, режимов его термообработки и величиной предельной рабочей нагрузки.

Материалы упругих элементов должны обладать высокими упругими свойствами, высокой прочностью при переменных нагрузках. Отдельные виды элементов должны быть стойкими к коррозии, иметь хорошую электропроводимость и антимагнитность.

Силовые и измерительные элементы изготавливают из высокоуглеродистых пружинных 65Г, 60С2, 70С2 и инструментальных У8, У10, У12 сталей.

Контактные и моментные антимагнитные, коррозионно-стойкие пружины (см. рис. 10.1, в, д) изготавливают из фосфористых БрОФ 6-0,15, БрОФ 4-0,2 и бериллиевой БрБ2 бронз.

Трубчатые манометрические пружины (рис. 10.1, и), сильфоны (рис. 10.1, е), мембраны и мембранные коробки (рис. 10.1, ж, з) изготавливают из латуней Л62, Л68, Л80, бронзы БрОФ4–0,2, нержавеющей стали Х18Н10Т.

Вид и режим термической обработки зависит от материала упругих элементов и требований к ним.

Наиболее широко из упругих элементов в приборо- и машиностроении используются винтовые пружины. Она просты и компактны по конструкции, надежны в работе. Их изготавливают путем холодной и горячей навивки проволоки с круглым, квадратным или прямоугольным поперечным сечением на специальные оправки.

По форме оправки винтовые пружины делятся на цилиндрические, конические и параболоидные, по виду нагружения – на пружины растяжения (рис. 10.3, а), сжатия (рис. 10.3, б, в) и кручения (рис. 10.3, г).

Основными размерами винтовых пружин являются: диаметр проволоки d; наружный диаметр D; средний диаметр витка пружины D_ср; шаг витков t; число витков i; длина пружины в свободном (ненагруженном) состоянии Н (для пружин сжатия и растяжения); индекс пружины c = D_ср / d.

F

в

д

г

б

а

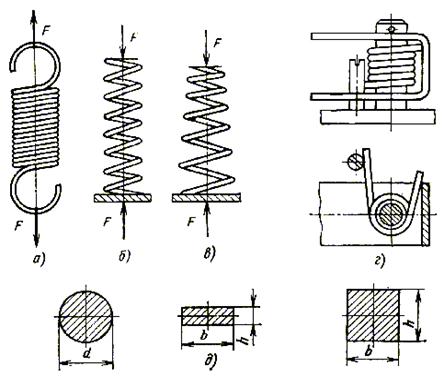
Рис. 10.3

С увеличением индекса с жесткость пружины снижается. Рекомендуется принимать индекс с = 16 … 8 при d < 0,4 мм; с = 12 … 6 при d = 0,4 … 2 мм и с = 10 … 4 при d > 2 мм.

Расчет пружины заключается в определении диаметра проволоки d, диаметра пружины D и числа витков i по заданной внешней нагрузке F и рабочему ходу f пружины.

Пружины растяжения навиваются с соприкасающимися витками (t = d). Изготавливают такие пружины двух видов: витки, соприкасаясь, не давят друг на друга, и витки, соприкасаясь, создают межвитковое давление. В последнем случае при навивке пружины проволоку скручивают вокруг ее оси. Пружина приобретает некоторое предварительное натяжение и начинает растягиваться только после приложения к ней нагрузки, большей предварительного натяжения.

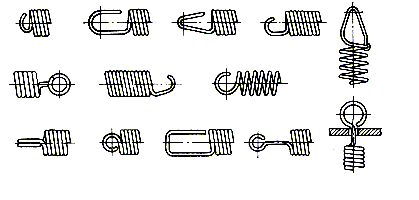
Рис. 10.4

Крайние витки пружин растяжения отогнуты и служат зацепами (рис. 10.4). Зацепы, часто являющиеся наиболее слабым местом пружины, имеют в зависимости от способа крепления различные формы. При растяжении зазоры между витками увеличиваются.

Пружины сжатия (см. рис. 10.3, б, в) изготавливают с зазором между витками. Крайние витки пружины всегда поджимают к соседним виткам и прошлифовывают по плоскости, перпендикулярной продольной оси. Это обеспечивает легкую установку пружины на опорной плоскости и центральное, т.е. строго по оси пружины, направление сжимающей нагрузки. Чтобы предотвратить возможную потерю устойчивости (выпучивание) пружины при соотношениях размеров Н / D >3, ее рекомендуют устанавливать в направляющем стакане или на стержне. Цилиндрические винтовые пружины сжатия получили наибольшее распространение, так как их форма сочетается с формой валиков, стаканов и других тел вращения. Винтовые конические пружины (см. рис. 10.3, в) обладают более высокой устойчивостью, в сжатом состоянии имеют минимальную высоту, но ввиду сложности изготовления применяются редко. Коническая пружина может сжиматься до размера, равного толщине проволоки, так как при сжатии виток входит в виток с небольшим зазором.

Пружины сжатия мало чувствительны к перегрузкам. Витки пружины при перегрузке полностью сжимаются, и пружина принимает вид жесткого цилиндра. Конические пружины сжатия применяют, если необходима нелинейная упругая характеристика.

Если при проектировании механизмов задача может быть решена путем применения пружины растяжения или пружины сжатия, то предпочтение отдают последней. При этом получают следующие преимущества: более простую конструкцию, чем у пружины растяжения; не требуются ограничители больших деформаций; поломка одного витка не ведет к мгновенному отказу механизма.

Винтовые пружины растяжения – сжатия имеют обычно линейную характеристику. При расчетных нагрузках материалы таких пружин работают в пределах упругих деформаций. Для устойчивости против вибрации и толчков винтовым пружинам в процессе сборки сообщается начальное нагружение F₀, т.е. пружину устанавливают в несколько растянутом или сжатом на величину f₀ состоянии.

Расчет цилиндрических винтовых пружин растяжения–сжатия выполняют по условиям прочности витков на кручение. Сортамент, механические свойства стальных углеродистых проволок, используемых для изготовления пружин, приведены в справочниках[7, 8]. Величину допускаемого напряжения материала при сдвиге (кручении) принимают ориентировочно при статической и пульсирующей нагрузке соответственно

t_adm = 0,4s_ut; t_adm = 0,2s_ut, (10.5)

где s_ut – предел прочности проволоки при растяжении.

Условие прочности в поперечных сечениях витков пружины

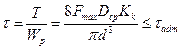, (10.6)

где T = (F_max ´ D_ср) / 2 – крутящий момент; F_max – максимальная нагрузка на пружину; W_p = pd³ / 16–полярный момент сопротивления поперечного сечения витка; 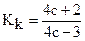– коэффициент, учитывающий концентрацию напряжений на поверхности витка и зависящий от величины индекса пружины с (с = D_ср / d); d, D_ср – соответственно диаметр проволоки и средний диаметр пружины.

Из уравнения (10.6) диаметр проволоки пружины равен

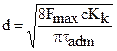(10.7)

или 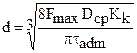. (10.8)

Исходными данными при расчете пружины являются начальная F₀ и максимальная F_max нагрузки, рабочая деформация f_p и характеристики проволоки: модуль упругости G и допускаемое напряжение t_adm при сдвиге.

Расчет осуществляется в следующем порядке:

1. Выбирают индекс пружины в пределах с = 4 … 16.

2. По формуле (10.7) определяют диаметр проволоки. Значение d принимают ближайшее большее по сортаменту. Средний и наружный диаметры пружины равны D_ср = cd; D = D_ср + d. Если внешний диаметр витков пружины ограничен, то диаметр проволоки определяют по формуле (10.8).

3. Вычисляют коэффициент жесткости пружины

. (10.9)

4. Определяют предварительную деформацию пружины

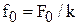. (10.10)

5. Число витков пружины рассчитывают по формуле

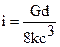(10.11)

или 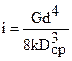. (10.12)

6. Определяют в недеформированном состоянии длину пружины:

растяжения H = id + h₃, (10.13)

сжатия H = i(d + e) + h_k + f_max, (10.14)

где h₃ – длина зацепов для крепления пружины растяжения; е = 0,5 мм – гарантированный зазор между витками пружины сжатия при максимальной деформации; h_k = (2 … 3) d – суммарная толщина нерабочих торцовых витков пружины; f_max = f_o + f_p.

7. Угол подъема витков пружины равен:

пружины сжатия 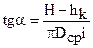, (10.15)

пружины растяжения 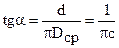. (10.16)

Этот угол не должен превышать 11 … 12°.

8. Определяют длину проволоки развернутой пружины:

сжатия 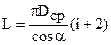, (10.17)

растяжения 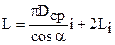, (10.18)

где L_i – длина заготовки зацепа пружины.

Винтовые пружины кручения (рис. 10.1, г) по внешнему виду отличаются от пружин растяжения–сжатия лишь конструкцией концевых витков. Один конец пружины (рис. 10.5) соединяется с неподвижной деталью, а другой – с подвижной и нагружается при этом усилием F на плече а. Концевые витки пружин отгибаются так, чтобы к ним можно было приложить моменты, действующие в плоскости витка. При закручивании пружины ее диаметр уменьшается, поэтому пружину устанавливают на цилиндрическую оправку диаметром d₀ с зазором, обеспечивающим свободный поворот витков. Пружины применяются для создания (рис. 10.1, г) противодействующего момента Т при закручивании свободного конца пружины на угол j. Их используют в виде силовых элементов, например, для поджатия магнитных и оптических головок записи и считывания информации.

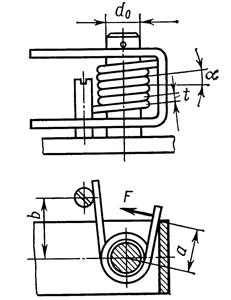
Рис. 10.5

Под действием момента Т (см. рис. 10.5, Т = F∙ a) в сечении проволоки возникает напряжение изгиба

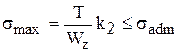, (10.19)

где W_z – момент сопротивления сечения относительно нейтральной оси, для круга диаметром d W_z = pd³ / 32» 0,1d³.

Коэффициент k₂ зависит от кривизны витка и определяется по следующей рекомендации: при с = 4 k₂ = 1,26; при с = 6 k₂ = 1,16; при с = 8 k₂ = 1,12 и при с = 10 k₂ = 1,1.

Диаметр проволоки d равен

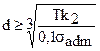. (10.20)

Для пружинных сталей, используемых при изготовлении пружин, допускаемое напряжение s_adm принимают 500 … 800МПа.

Диаметр витка пружины D = (c + 1)d.

Угол закручивания пружины из круглой проволоки

j = T×ℓ / (EI_z) = 64T×ℓ / (Epd⁴), (10.21)

где ℓ = pD_ср×i –развернутая длина проволоки витков пружины; EI_z – жесткость проволоки на изгиб, I_z = pd⁴ / 64.

Из формулы (10.21) задавая угол закручивания, определяют длину и число витков пружины i. При определении длины развернутой проволоки пружины L необходимо учитывать и длину концов. Шаг t пружины (рис. 10.5) на 0,3 … 0,5 мм больше диаметра витков, а высота H будет равна H = i t.

Дата добавления: 2014-11-29