
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Логические задачи в алгебре Буля
|
|
|
|
Лабораторная работа №5
В настоящее время методы математической логики внедряются в гуманитарные знания как аппарат, позволяющий быстро и эффективно перерабатывать огромные объемы информации. Эти методы, как правило, при объяснении понятий и существующих между ними отношений исключают ошибки, проистекающие за счет неточного толкования смысла понятий, благодаря использованию логических операций.
Впервые с идеей внедрения логики и математики в процесс познания закономерностей между объектами любой природы выступил немецкий философ и математик Лейбниц (1646-1716). Он предвидел возникновение новой области науки, названной им философским исчислением.
Философское исчисление, по идее Лейбница, должно представлять такую логическую систему, в которой все производные понятия выражались бы символами, составленными из известных простых символов, обозначающих элементарные понятия на основании строгих правил. Операции над символами должны производиться по аналогии с алгебраическими операциями так, чтобы формальным путем можно было получать все новые и новые понятия и умозаключения.
Грандиозный замысел Лейбница долгое время оставался без развития. Первый крупный шаг в осуществлении идей Лейбница был сделан Джорджем Булем (1815-1864). В период с 1847 по 1857 г. он опубликовал три работы. Первые две носили характер предварительных исследований. В третьей работе (это объемистая книга в 424 стр.) изложена, в сущности, вся система Буля. Здесь он демонстрирует, как при помощи символических алгебраических методов можно строить логические конструкции. Кроме того, он показывает, как его система может быть распространена на теорию вероятностей.
В этих работах Буль преследует еще одну цель: найти элементарные операции человеческого мышления, выйдя за рамки дедуктивной и индуктивной логики. Выражаясь современным языком, его исследования принадлежали к области кибернетики.
Буль впервые показал, что законы человеческого мышления могут быть формализованы так, что над понятиями могут производиться те же операции, что и над целыми числами. Но в отличие от арифметики, как он показал, формальные операции над понятиями подчиняются следующим двум законам: два одних и тех же понятия сложенные или перемноженные приводят к тому же понятию (в современной Булевой алгебре их называют – отсутствие коэффициентов и степеней).
На формирование Булевой алгебры как самостоятельной научной дисциплины оказали влияние исследования немецкого математика Эрнста Шредера (1841-1902), который дал математическую трактовку закона исключенного третьего аристотелевской логики.
Шредер допускал наличие классов больше двух и для оперирования с ними он сформулировал следующее правило: если среди членов некоторой суммы классов находится хотя бы один, который оказывается отрицанием другого, то вся сумма равна единице. Легко показать, что с помощью этого правила можно построить таблицу операции отрицания Булевой алгебры.
Символическое исчисление Буля Шредер называл логическим исчислением и признавал только три основных операции: сложение, умножение и отрицание; вычитание он считал не безусловно выполнимой операцией. Тем самым Шредер поставил вопрос об оптимальном количестве операций в логике классов.
Однако гениальная догадка Буля состояла в том, что только на множестве числа М={0;1} символическое исчисление не противоречит опыту человеческого мышления. Вопрос же об оптимальности количества операций и в логике классов, и в исчислении Буля решается неоднозначно.
Согласно современным представлениям, алгеброй Буля 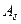 называют элементы множества М={0;1} с заданными в нем операциями S={“Ú”,“Ù”,“-“} дизъюнкции, конъюнкции и отрицания. Обозначается алгебра Буля так:
называют элементы множества М={0;1} с заданными в нем операциями S={“Ú”,“Ù”,“-“} дизъюнкции, конъюнкции и отрицания. Обозначается алгебра Буля так: 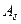 =(М;S), здесь М – множество, S – сигнатура алгебры, т.е. набор операций. Переменные
=(М;S), здесь М – множество, S – сигнатура алгебры, т.е. набор операций. Переменные 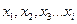 будем называть булевыми переменными. Эти переменные обозначают понятия или высказывания как неделимые понятия, если
будем называть булевыми переменными. Эти переменные обозначают понятия или высказывания как неделимые понятия, если 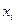 =0, то высказывание ложно, если же
=0, то высказывание ложно, если же 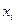 =1, высказывание истинно.
=1, высказывание истинно.
Рассмотрим следующие логические задачи, которые решаются на базе символического исчисления Буля.
Задача 1. Алеша, Боря и Гриша нашли в земле сосуд. Рассматривая удивительную находку, каждый высказал по два предложения:
Алеша. Это сосуд греческий и изготовлен в 5 веке.
Боря. Это сосуд финикийский и изготовлен в 3 веке.
Гриша. Это сосуд не греческий и изготовлен в 4 веке.
Учитель истории сказал ребятам, что каждый из них прав только в одном из двух предложений.
Где и в каком веке изготовлен сосуд?
С помощью Булевой переменной введем обозначения:
- Это сосуд греческий – 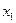 ;
;
- Изготовлен в 5 веке – 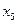 ;
;
- Это сосуд финикийский – 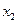 ;
;
- Изготовлен в 3 веке – 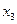 ;
;
- Это сосуд не греческий – 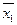 ;
;
- Изготовлен в 4 веке – 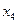 .
.
В этих обозначениях высказывания ребят кодируются логическими функциями следующим образом
Алеша: 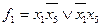
Боря: 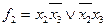
Гриша: 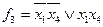
Кроме того, ясно, что сосуд может быть изготовлен только в одном из веков и только в одной из стран. Эти условия позволяют ввести дополнительные логические функции:
 ,
,
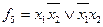

Полученные таким образом логические функции 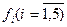 представлены в совершенной дизъюнктивной нормальной форме. Если придать всевозможные значения наборам переменных, от которых зависят указанные функции, то можно получить таблицы для
представлены в совершенной дизъюнктивной нормальной форме. Если придать всевозможные значения наборам переменных, от которых зависят указанные функции, то можно получить таблицы для 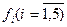 .
.
Будем считать все 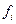 =1, тогда получим следующую систему уравнений Булевой алгебры
=1, тогда получим следующую систему уравнений Булевой алгебры
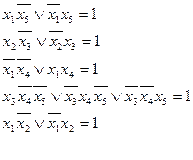 (1)
(1)
Система (1) представляет математическую модель искомой задачи. Один из способов решения (1) состоит в подборе тех единичных термов логических функций 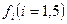 , наборы переменных которых удовлетворяют системе (1), а значения переменных
, наборы переменных которых удовлетворяют системе (1), а значения переменных 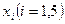 из этих наборов не противоречат друг другу.
из этих наборов не противоречат друг другу.
Для нахождения всех единичных термов системы (1) необходимо произвести вычисление таблиц функций f 1, f 2, f 3, f 4, f 5. Это можно сделать с помощью программы Microsoft Excel. Для этого:
1. Включите компьютер;
2. После того, как на экране монитора появится рабочий стол операционной системы Windows, откройте окно Microsoft Excel;
3. Заполните ячейки A1¸B4 таблицы, перебрав все варианты значений логических переменных х1 и х5;
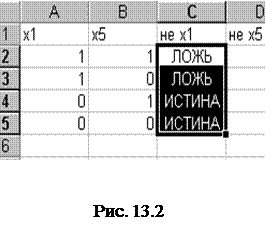
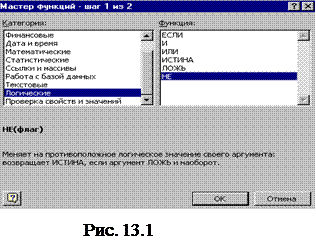
4. Постройте таблицу истинности для функции f 1, воспользовавшись функциями НЕ, И, ИЛИ, которые находятся в мастере функций ƒх в категории ЛОГИЧЕСКИЕ. Для этого:
активизируйте ячейку С2;
воспользуйтесь функцией НЕ (см. рис. 13.1);
автозаполнением занесите полученные результаты в ячейки С2¸С5 (рис. 13.2)
5. 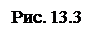 Аналогичным способом достроим
Аналогичным способом достроим 
6. таблицу истинности для функции f 1, используя функции И, ИЛИ. В результате получим значения для х1 и х5, изображённые на рис. 13.3.
Строя таблицы для функций f 2 – f 5 и, проводя аналогичные действия с переменными, получим следующие таблицы (рис. 13.4):
Таблица 1. Таблица 2. Таблица 3.
| x1 | x5 | f 1 | x2 | x3 | f 2 | x1 | x4 | f 3 | |||
Таблица 4. Таблица 5.
| x3 | x4 | x5 | f 4 | x1 | x2 | f 5 | |
В таблицах 1 – 5 единичные наборы определяются теми наборами переменных, при которых логические функции имеют единичные значения. Для решения поставленной задачи необходимо выбрать пять единичных термов, значения переменных в которых не противоречивы.
В качестве таковых наборов переменных возьмём следующие:
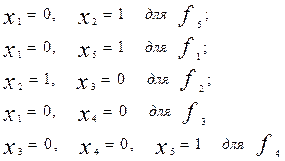
Из этих наборов переменных следует, что решение имеет вид:
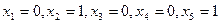 (2)
(2)
Непротиворечивость решения (2) надо понимать так: значение х1=0 имеет место в наборах переменных для функций f 5, f 1, f 3 аналогично х5=1 имеет место для f 1, f 4 и т.д.
Для проверки решения (2) подставим его в систему (1) и убедимся в том, что после этого уравнения системы (1) превращаются в тождества.
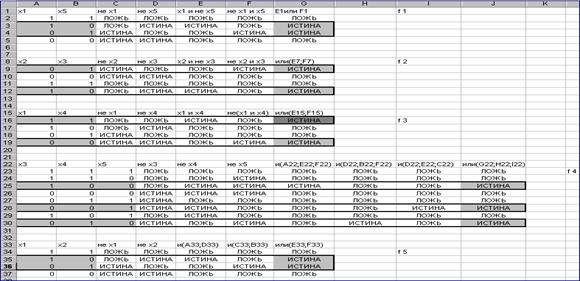
Рис. 13.4
Для воспроизведения решения (2) в словесной форме необходимо вспомнить высказывания, которые кодировались символами х i. Из принятой кодировки следует, что х2=1 означает, что сосуд – финикийский, а х5=1 – сосуд изготовлен в 5-ом веке.
Задача 2. В школе произошло чрезвычайное происшествие: в классе кто-то из учеников разбил окно. Учителем были опрошены четыре ученика— Лёня, Дима, Толя и Миша. Каждый из учеников сделал по три заявления (см. таблицы 1 – 4). Учитель усомнился в одном из трёх заявлений каждого из опрошенных учеников. Последнее означает, что у каждого одно из трёх заявлений неверно. Из анализа всех заявлений необходимо узнать— кто разбил окно.
Таблица 6.
| № | Показания Лёни | События | Вероятности | Переменные |
| Я не виноват. | 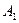
| 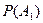
| 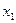
| |
| Я не подходил к окну. | 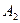
| 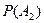
| 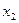
| |
| Миша знает, кто разбил окно. | 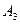
| 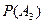
| 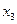
|
Таблица 7.
| № | Показания Димы | События | Вероятности | Переменные |
| Стекло разбил не я. | 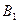
| 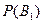
| 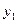
| |
| С Мишей я не был знаком до поступления в школу. | 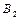
| 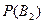
| 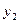
| |
| Это сделал Толя. | 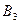
| 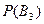
| 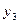
|
Таблица 8.
| № | Показания Толи | События | Вероятности | Переменные |
| Я не виноват. | 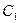
| 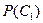
| 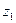
| |
| Это сделал Миша. | 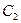
| 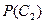
| 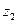
| |
| Дима говорит неправду, что я разбил окно. | 
| 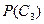
| 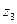
|
Таблица 9.
| № | Показания Миши | События | Вероятности | Переменные |
| Я не виноват. | 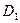
| 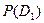
| 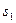
| |
| Стекло разбил Лёня. | 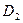
| 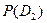
| 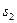
| |
| Дима может поручиться за меня. | 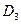
| 
| 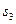
|
Для получения вычислимого логического алгоритма решения данной задачи необходимо формализовать её условие, т.е. показаниям всех учеников придать форму математических соотношений, состоящих из символов, обозначающих понятия, и знаков логических операций, выполняемых над указанными символами.
С этой целью предположим, что каждое из показаний Лёни есть события 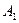 ,
, 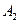 ,
, 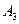 , которые могут произойти или не произойти. Вероятности того, что каждое из названных событий имело место, обозначим соответственно
, которые могут произойти или не произойти. Вероятности того, что каждое из названных событий имело место, обозначим соответственно 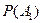 ,
, 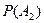 ,
, 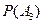 . Вероятности же того, что события не имели место, обозначим через
. Вероятности же того, что события не имели место, обозначим через 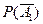 ,
,  ,
, 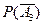 . При этом предполагается, что событие
. При этом предполагается, что событие 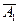 противоположно событию
противоположно событию 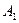 и т.д. применительно к оставшимся событиям.
и т.д. применительно к оставшимся событиям.
Событие 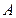 , состоящее в том, что из трёх показаний Лёни одно не верно, называется сложным событием. Оно составляется как комбинация простых событий следующим образом:
, состоящее в том, что из трёх показаний Лёни одно не верно, называется сложным событием. Оно составляется как комбинация простых событий следующим образом: 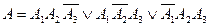 (3)
(3)
Здесь операция суммы событий заменена операцией дизъюнкции, а операция произведения— конъюнкцией. Такие законы обоснованы выше. Вероятность сложного события 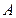 обозначим через
обозначим через 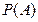 . В теории вероятностей значения вероятности могут принимать весь спектр числовых значений от нуля до единицы. Применительно к данной задаче будем считать, что вероятности Р принимают только предельные значения: нуль или единица. Это позволяет отождествлять вероятность
. В теории вероятностей значения вероятности могут принимать весь спектр числовых значений от нуля до единицы. Применительно к данной задаче будем считать, что вероятности Р принимают только предельные значения: нуль или единица. Это позволяет отождествлять вероятность 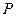 с Булевой переменной
с Булевой переменной 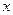 , т.е. ввести обозначения:
, т.е. ввести обозначения: 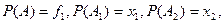
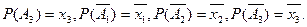 В этом случае
В этом случае 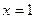 означает истинность данного события, а
означает истинность данного события, а 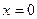 — ложность. Аналогично
— ложность. Аналогично 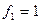 говорит об истинности сложного события
говорит об истинности сложного события 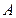 , а
, а 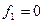 — об его ложности.
— об его ложности.
Теперь, согласно теоремам о вероятности суммы и произведения нескольких событий, вероятность  сложного события
сложного события  определяется следующим образом:
определяется следующим образом: 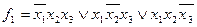 (4)
(4)
Проводя аналогичные рассуждения для показаний остальных учеников, и используя обозначения таблиц 2 – 4, заявления Димы, Толи и Миши представим в форме следующих математических соотношений:
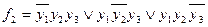 (5)
(5)
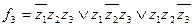 (6)
(6)
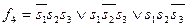 (7)
(7)
Все эти логические формулы однотипны и представляют совершенную дизъюнктивную нормальную форму (СДНФ) одной и той же логической функции 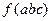 .
. 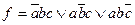 (8)
(8)
Придавая набору, 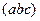 различные комбинации из нулей и единиц, подставляя их в (8) и производя вычисления с помощью таблиц операций конъюнкции и дизъюнкции, получаем таблицу 10 логической функции
различные комбинации из нулей и единиц, подставляя их в (8) и производя вычисления с помощью таблиц операций конъюнкции и дизъюнкции, получаем таблицу 10 логической функции 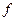 .
.
Таблица 5.
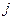
| 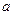  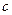
| 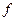
|
| 0 0 0 0 0 1 0 1 0 0 1 1 | ||
| 1 0 0 1 0 1 1 1 0 1 1 1 |
В таблице 10 через 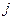 обозначен десятичный код набора переменных, представляющего множество трёхразрядных двоичных чисел.
обозначен десятичный код набора переменных, представляющего множество трёхразрядных двоичных чисел.
Единичные значения логической функции 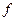 называются единичными термами. Для них введём новое обозначение
называются единичными термами. Для них введём новое обозначение 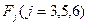 .
.
Единичные термы можно вычислять с помощью операций конъюнкции и отрицания по следующим формулам:
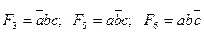 (9)
(9)
Поскольку в формулах (9) главной операцией считается операция конъюнкции, то единичные термы называют конъюнктивными термами. Если три конъюнктивных терма объединить знаком дизъюнкции, то согласно теории логических функций, получим аналитическое представление функции в форме СДНФ (8).
Для получения явного вида конъюнктивных термов логических функций 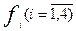 необходимо вычислить таблицы этих функций с помощью программы Microsoft Excel. Для этого:
необходимо вычислить таблицы этих функций с помощью программы Microsoft Excel. Для этого:
7. В окне Microsoft Excel заполните ячейки А12¸С49 таблицы, перебрав все варианты значений логических переменных хj, уj, zj и sj;
Постройте таблицу истинности для функций Fij, воспользовавшись функциями НЕ, И, ИЛИ, которые находятся в мастере функций ƒх в категории ЛОГИЧЕСКИЕ. См. пп. 4 – 5.
В конечном итоге получаем таблицу, показанную на рис. 13.5.
Из таблицы, изображённой на рис. 13.5, формируем таблицу 11, состоящую из конъюнктивных термов функций 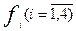 и соответствующих им наборов переменных.
и соответствующих им наборов переменных.
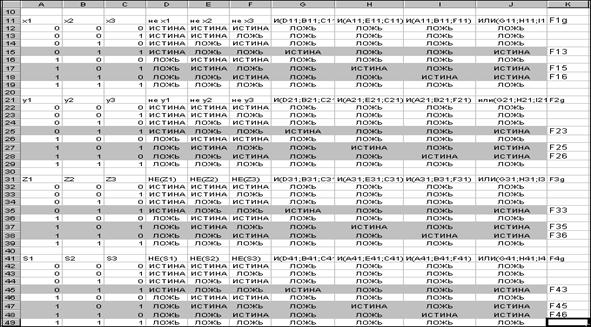
Рис. 13.5
Таблица 11.
| f1 | f2 | f3 | f4 | ||||||||||||
| x1 | x2 | x3 | F1J | y1 | y2 | y3 | F2J | z1 | z2 | z3 | F3J | s1 | s2 | s3 | F4J |
| F13 | F23 | F33 | F43 | ||||||||||||
| F15 | F25 | F35 | F45 | ||||||||||||
| F16 | F26 | F36 | F46 |
Здесь применительно к функции fi конъюнктивный терм обозначен через FiJ так, что верхний индекс i соответствует номеру логической функции.
Если никто из учеников не отказался от своих высказываний, то значение всех логических функций 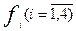 надо положить равными единице, после чего соотношения (4) – (7) примут вид следующей системы алгебраических уравнений для определения двенадцати неизвестных, которые представляются показаниями учеников в обозначениях таблиц 6 – 9:
надо положить равными единице, после чего соотношения (4) – (7) примут вид следующей системы алгебраических уравнений для определения двенадцати неизвестных, которые представляются показаниями учеников в обозначениях таблиц 6 – 9:
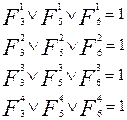 (10)
(10)
Здесь для обозначения конъюнктивных термов, входящих в 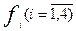 использован символ
использован символ 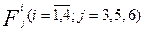 . Соотношения (10) представляют математическую модель показаний учеников и их следует называть системой уравнений Булевой алгебры, так как они определены на множестве М={0;1} с использованием трёх логических операций – дизъюнкции, конъюнкции и отрицания.
. Соотношения (10) представляют математическую модель показаний учеников и их следует называть системой уравнений Булевой алгебры, так как они определены на множестве М={0;1} с использованием трёх логических операций – дизъюнкции, конъюнкции и отрицания.
В этой системе число неизвестных превышает число уравнений. Однако, так как 1Ú0=1, то решение системы (10) будет определяться такими четырьмя термами: F1 j, F2 j, F3 j, F4 j, (j=3, 5, 6), наборы переменных, которых после подстановки в (10) и проведения логических вычислений превратят уравнение (10) в тождества. При этом термы FiJ вычисляются по формуле (9) с учётом обозначения переменных согласно таблице 11.
Среди комбинаций из указанных четырёх термов могут оказаться такие, значения наборов переменных которых могут привести к противоречивым показаниям учеников. Например, рассмотрим термы F13, F23, F33, F43.
Наборы переменных, соответствующие указанным термам, определяются по таблице 11. В таблице 12 приведены значения переменных, найденные из полученных наборов переменных, а также показания учеников, соответствующие данным значениям переменных.
Чтобы показать, что значения переменных из таблицы 12 суть решение системы (10) необходимо для этих значений вычислить по (9) строки и подставить их в тождества.
Здесь же в таблице 12 даются высказывания мальчиков, соответствующие рассмотренному решению. Из них следует, что все ученики виноваты. Последнее противоречит условию задачи.
Такое решение задачи в дальнейшем будем называть противоречивым
Таблица 12.
| F13=1 | Показания Лёни. |
| x1=0 x2=1 x3=1 | Я виноват. Я не подходил к окну. Миша знает, кто разбил окно. |
| F23=1 | Показания Димы. |
| y1=0 y2=1 y3=1 | Стекло разбил я. С Мишей я не был знаком до поступления в школу. Это сделал Толя. |
| F33=1 | Показания Толи. |
| z1=0 z2=1 z3=1 | Я виноват. Это сделал Миша. Дима говорит неправду, что я разбил окно. |
| F43=1 | Показания Миши. |
| s1=0 s2=1 s3=1 | Я виноват. Стекло разбил Лёня. Дима может поручиться за меня. |
Рассмотрим другое решение: F13=1, F26=1, F35=1, F46=1. Значения переменных и показания учеников, соответствующие этому решению, приведены в таблице 13.
Таблица 13.
| F13=1 | Показания Лёни. |
| x1=0 x2=1 x3=1 | Я виноват. Я не подходил к окну. Миша знает, кто разбил окно. |
| F26=1 | Показания Димы. |
| y1=1 y2=1 y3=0 | Стекло разбил я. С Мишей я не был знаком до поступления в школу. Это не сделал Толя. |
| F35=1 | Показания Толи. |
| z1=1 z2=0 z3=1 | Я не виноват. Это не сделал Миша. Дима говорит неправду, что я разбил окно. |
| F46=1 | Показания Миши. |
| s1=1 s2=1 s3=0 | Я не виноват. Стекло разбил Лёня. Дима не может поручиться за меня. |
Непротиворечивые показания этой таблицы говорят о том, что Лёня виноват и он разбил окно.
Решение, приводящее к логически непротиворечивому результату, назовём непротиворечивым.
Возникает вопрос: Как из множества решений выбрать одно – непротиворечивое?
Вернёмся к первоначальным заявлениям учеников (таблицы 6 – 9) и обратим внимание на то, что из четырёх заявлений – x1, y1, z1, s1 одно не верно.
По аналогии с рассуждениями, приводящими к формулам (3) и (4), указанную особенность четырёх заявлений можно выразить так:
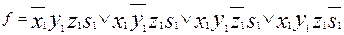 (11)
(11)
Теперь значения переменных из таблицы 13 подставим в правую часть формулы (11) и произведём вычисление f с помощью программы Microsoft Excel. Для этого:
8. В ячейках А52 – D52 запишите значения переменных x1, y1, z1 и s1 из таблицы 13.
9. Далее, с помощью функций НЕ, И, ИЛИ найдём значение функции f.
В данном случае получим: f = f max=1.
10. Аналогично вычислим f по (11) с использованием значений переменных из таблицы 12; тогда будем иметь: f = f min=0 (рис. 13.6).

Рис. 13.6
Таким образом, непротиворечивое решение приводит к максимальным значениям логической функции (11). Последнее может означать, что логическая функция (11) представляется критерием отбора непротиворечивого решения системы (10) из множества решений. По аналогии с экономическими задачами линейного и нелинейного программирования, логическую функцию (11) следует назвать целевой функцией.
Теперь алгоритм решения данной задачи (10) – (11) сводится к следующему: перебираем всевозможные комбинации из четырёх термов F1 j, F2 j, F3 j, F4 j, затем применительно к каждой выбранной комбинации по таблице 11 определяем значения переменных, по которым вычисляем целевую функцию (11).
Тот вариант из четырёх единичных термов, который определит максимальное значение целевой функции (11), следует признать в качестве непротиворечивого решения.
Очевидно, что такой алгоритм требует большого объёма логических вычислений. Так, например, в рассматриваемой задаче, число комбинаций из четырех термов будет определяться числом сочетаний из двенадцати термов по четыре, т.е. 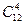 =495
=495
Задания для самостоятельной работы.
Задача 1. На заводе работали три друга: слесарь (с), токарь (т), шлифовщик (ш). Их фамилии: Борисов (Б), Иванов (В), Семенов (С).
Дополнительные сведения об указанных лицах таковы:
1 – у слесаря нет ни братьев, ни сестер;
2 – слесарь самый младший из друзей;
3 – Семенов женат на сестре Борисова;
4 – Семенов старше токаря.
Необходимо узнать: у кого какая специальность?
Ответ: Семенов – шлифовщик; Иванов – слесарь; Борисов – токарь.
Задача 2. В одном королевстве были незамужние принцессы, голодные тигры и приговоренный к казни узник. Но всякому узнику, осужденному на смерть полагалось угадать, в какой из двух комнат находиться тигр, а в какой принцесса. Хотя вполне могло быть, что король в обеих комнатах разместил принцесс, или что хуже, в обеих – тигров. Выбор надо было сделать на основании табличек на дверях комнат. Причём узнику было известно, что утверждения на табличках либо оба истинны, либо оба ложны. Надписи гласили:


Какую дверь должен выбрать узник?
Ответ: в первой комнате – тигр, во второй – принцесса.
Задача 3. На соревнованиях по лёгкой атлетике Андрей, Боря, Серёжа и Володя заняли первые четыре места. Но когда девочки стали вспоминать, как эти места распределились между победителями, то мнения разошлись:
Даша: Андрей был первым, а Володя – вторым.
Галя: Андрей был вторым, а Борис – третьим.
Лена: Боря был четвёртым, а Серёжа – вторым.
Ася, которая была судьёй на этих соревнованиях и хорошо помнила как распределились места сказала, что каждая из девочек сделала одно правильное и одно неправильное заявление.
Кто из мальчиков и какое место занял?
Ответ: Андрей занял первое место, Серёжа – второе, Боря – третье, Володя – четвёртое.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 986; Нарушение авторских прав?; Мы поможем в написании вашей работы!