Размещения

Множество вместе с заданным порядком расположения его элементов называют упорядоченным множеством.

Пример. Дано множество .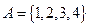

Подмножества 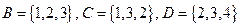-- это различные упорядоченные множества.

Каждое упорядоченное подмножество из m элементов множества из n элементов называется размещением из n элементов по m элементов -- («A из n по m»).

Теорема. Число размещений элементов множества определяется по формуле: .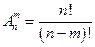

Для доказательства данной формулы воспользуемся следующими рассуждениями: на первое место упорядоченного множества из m элементов можно поставить один из n элементов (таких вариантов n), на второе – один из (n-1) элементов (таких вариантов (n-1)). Итого n(n-1), т.к. каждому из n соответствует один из (n-1). Продолжая далее, на m место можно поставить один из (n-m+1). Получаем: .

Пример: Сколько различных размещений по 3 элемента из элементов множества 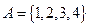можно составить?

.

Бывают случаи, когда элементы в m-подмножествах повторяются. Такие размещения называют размещениями с повторениями.

Теорема. Число размещений из n элементов множества по m с повторениями равно .

Действительно, поскольку осуществляется m выборов и каждый производится из n элементов, то по правилу произведения получаем .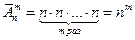

Пример: Сколькими способами можно распределить 3 различных предмета между 5 лицами?

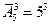=125.

Задачи.

1. Доказать, что .

2. Сколькими способами можно выбрать четырех человек на четыре различные должности из девяти кандидатов на эти должности?

3. В группе 15 студентов. Они обменялись друг с другом фотокарточками. Сколько всего было роздано фотокарточек?

4. Найти n, если .

5. Какая часть из 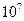семизначных телефонных номеров состоит из семи различных цифр?

6. В однокруговом турнире по футболу участвуют 8 команд. Сколько существует вариантов призовой тройки?

7. Студенты первого курса изучают 15 предметов. Сколькими способами можно составить расписание на среду, если известно, что в этот день должно быть 6 пар?

8. Сколько различных слов из 3 букв можно составить из 33 букв алфавита?

9. Сколько существует вариантов назначения 5 исполнителей на выполнение 5 видов работ?

3.4. Сочетания.

Пример: Рассмотрим все подмножества множества 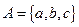. Их восемь:

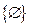-- пустое множество;

-- три множества по одному элементу в каждом;

-- три множества по два элемента в каждом;

-- одно множество из трех элементов.

Число подмножеств по m элементов в каждом, содержащихся в множестве из n элементов, обозначается 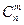. В комбинаторике конечные множества называются сочетаниями. Поэтому 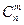называют «числом сочетаний из n по m».

Из примера видно, что и

.

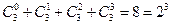Если число элементов множества большое, то процесс выписки всех подмножеств сложен. В этом случае число подмножеств определяется по формуле P(A)= . Выведем ее.

Перенумеровав все элементы множества А из примера, поставим в соответствие каждому подмножеству комбинацию 0 и 1, где присутствие элемента означает 1, отсутствие – 0. Т.е. 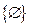-- 0,0,0;

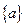-- 1,0,0;

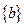-- 0,1,0 и т.д.

Таким образом, проблема о количестве подмножеств n-элементного множества А сводится к тому, сколько различных последовательностей длины n можно построить из 0 и 1. По правилу умножения, их число будет равно .

Чтобы вывести формулу для 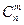, докажем сначала, что .

Рассмотрим случай при m=2 и n=3. 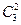=3 – число множеств по две буквы в каждом. Каждое из них можно упорядочить 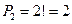способами, что дает 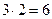упорядоченных множеств. Действительно, .

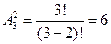Общее доказательство аналогично. Чтобы образовать упорядоченное множество, содержащее m элементов из данных n, надо:

-- выделить какие-либо m из этих n элементов, что можно сделать 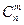способами;

-- упорядочить выделенные m элементы, что можно сделать 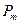способами.

Всего получим 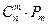способов (упорядоченных множеств), т.е.

, что и требовалось доказать.

Из этой формулы несложно получить .

Подставляя сюда формулы и 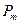, получим:

.

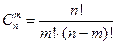Пример: Сколькими способами можно выбрать трех делегатов на конференцию из 35 студентов?

.

Основные свойства сочетаний:

;

;

;

.

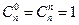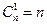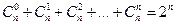Сочетаниями с повторениями называют такие сочетания, в которых элементы могут повторяться.

Пример: в почтовом отделении продаются открытки 5 видов. Определить число способов покупки 7 открыток.

.

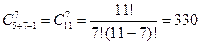Теорема. Число сочетаний 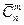из n элементов по m c повторениями определяется по формуле .

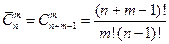Числитель (n+m-1) составляется таким образом потому, что каждому из сочетаний ставится в соответствии комбинация из m единиц и n-1 нулей, по которой в обратном порядке можно восстановить соответствующее сочетание. Знак факториала означает число всех возможных перестановок элементов этих комбинаций. В итоге формула числа сочетаний с повторениями соответствует формуле числа перестановок с повторениями , в которой n=n+m-1, .

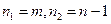Кроме решения различного вида комбинаторных задач сочетания используются также в алгебраических вычислениях: .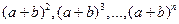

Для положительного целого числа n справедлива формула, называемая биномом Ньютона:

, где 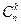-- биномиальные коэффициенты.

Пример: .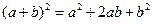

Задачи.

1. Составить все подмножества множества М и найти их число, если:

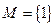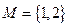а) ; б) ; в) .

2. Сколько подмножеств содержит множество из 6 элементов?

3. Найти: а) 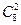; б) ; в) .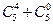

4. Из 20 рабочих нужно выделить 6 для работы на определенном участке. Сколькими способами это можно сделать?

5. Сколькими способами можно группу из 15 учащихся разделить на две группы так, чтобы в одной группе было четыре человека, а в другой – одиннадцать?

6. Сколько человек участвовало в шахматном турнире, если известно, что каждый участник сыграл с каждым из остальных по одной партии, а всего было сыграно 210 партий.

7. Студент имеет по одной монете достоинством 5 коп., 10 коп., 50 коп., 1 руб., 2 руб., 5 руб., 10 руб. Сколькими способами он может разложить эти монеты в два кармана?

8. Из 10 различных цветов нужно составить букет так, чтобы он состоял из не менее двух цветов разного сорта?

9. Имеется 12 различных конфет. Сколькими способами можно из них составить набор, если в наборе должно быть четное число конфет?

10. Сколько существует способов выбора в кондитерской шести пирожных из восьми их сортов?

11. Сколько костей домино можно сделать, используя 7 цифр?

12. Определить разложение при n=5.

Глава 4. Теория графов.

Дата добавления: 2014-11-29