Построение коммуникационной сети минимальной длины

Задача о кратчайшем пути между двумя пунктами.

Задача определения кратчайшего пути.

Задача состоит в том, чтобы найти кратчайший путь на графе от какой-то выделенной вершины до любой другой.

Пример: узел 7 – склад, остальные узлы – строительные площадки компании. Показатели на дугах расстояния в километрах.

Надо найти кратчайшие расстояния от склада до каждой строительной площадки. Какова длина кратчайшего пути от склада до строительной площадки 1? Проходит ли кратчайший путь от склада до строительной площадки 1 через строительную площадку 2?

Решим эту задачу методом присвоения меток. Каждому узлу присваиваем метку из двух чисел. Первое число – это минимальное расстояние от узла 7 до данного узла, второе – номер предыдущего узла. Если кратчайшее расстояние от узла 7 определено, то соответствующая метка называется постоянной. Она закрашивается и обозначается круглыми скобками. Все остальные метки – временные, обозначаются квадратными скобками.

Изначально узлу 7 присваиваем метку (0,S), где 0 – расстояние от узла 7 – обозначение стартового узла.

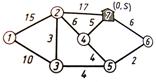
Узел 7 связан с узлами 2,4,6. Длины соответствующих ребер – 17,5,6. Поэтому узлам 2,4,6 присваиваем временные метки -- .

Временная метка с наименьшим расстоянием до узла 7 становится постоянной. Это метка (5,7) узла 4. Поэтому следующий шаг начинаем с узла 4.

Узел 4 связан с узлами 2 и 5 без постоянных меток. Длина ребра 4 -- 5 равна 4, метка узла 4 – (5,7) временная метка узла 5 равна . Длина ребра 4 -- 2 равна 6, метка узла 4 – (5,7) временная метка узла 2 равна . Узел 2 помечен меткой , но 11<17 старую метку узла 2 меняем на новую временную метку , где 11 – длина пути от узла 7 до узла 2, 4 – номер предшествующего узла.

После этого из всех временных меток выбираем метку с наименьшим первым числом. Это . Эта метка становится постоянной, а очередной шаг начинаем с узла, соответствующего этой метке, -- узла 6.

Этот узел связан с узлом 5 без постоянной метки. Длина ребра 6-5 равна 2, метка узла 6 – (6,7) временная метка узла 5 равна . Но узел 5 уже помечен меткой 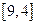. Так как 8<9, то узлу 5 припишем новую метку . После этого из всех временных меток 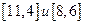метку с наименьшим первым числом объявим постоянной, а следующий шаг начнем с соответствующего ей узла 5.

Узел 5 связан только с одним узлом без постоянной метки – узлом 3. Длина ребра 5-3 равна 4, метка узла 5 -- временная метка узла 3 равна . Теперь из временных меток 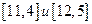метку с наименьшим первым числом объявляем постоянной, а следующий шаг начнем с соответствующего ей узла 2.

Узел 2 связан с узлами 1 и 3 без постоянных меток. Длина ребра 2-1 равна 15, метка узла 2 -- узлу 1 припишем временную метку . Длина ребра 2-3 равна 3, метка узла 2 -- можно пометить узел 3 временной меткой , но узел 3 уже помечен меткой с меньшим первым числом. Поэтому метку 3 не меняем. Теперь из временных меток 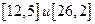метка с наименьшим первым числом становится постоянной , а с соответствующего ей узла 3 начнем следующий шаг. Метку узла 1 меняем на . Всем узлам приписаны постоянные метки. Действие алгоритма прекращается.

Первое число метки у каждой вершины – это длина кратчайшего пути от узла 7 до данной вершины. Чтобы восстановить кратчайший путь от узла 7 до какой-то вершины, нужно из этой вершины перейти в соседнюю (ее номер – это второе число метки). И так до вершины 7.

Теперь можно ответить на вопросы задачи. Метка узла 1 -- длина кратчайшего пути от узла 7 до узла 1 равна 22. Из узла 1 идем в узел 3. Метка узла 3 -- идем в узел 5. Метка узла 5 -- идем в узел 6. Метка узла 6 -- идем в узел 7, т.е. кратчайший путь 1-3-5-6-7. Он не проходит через узел 2.

Задачи.

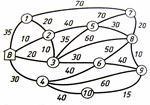
1. Компания грузовых перевозок осуществляет услуги по перевозке грузов между Воронежем (В) и райцентрами. Так как существенны быстрое обслуживание и минимальные транспортные затраты, то необходим наиболее короткий маршрут. Рисунок отображает сеть дорог. Расстояния указаны в километрах. Найти кратчайшие маршруты от Воронежа до всех 10 райцентров. Какова длина кратчайшего пути от Воронежа до райцентра 10? Проходит ли кратчайший путь от Воронежа до райцентра 9 через райцентр 6?

2. Предложить алгоритм действий при наличии в сети нескольких равных постоянных меток.

Известна схема дорог. Требуется перевезти груз из одного пункта в другой по маршруту минимальной длины.

Пример: Найдем маршрут минимальной длины от пункта 1 к пункту 11.

Припишем вершинам числа вместо номеров. Для 11-й вершины это 0.

11-я вершина соединена с 8-й, 9-й и 10-й вершинами, которым припишем числа 0+5=5, 0+5=5, 0+4=4 соответственно. Все эти ребра покажем двумя чертами со стрелками.

По числам 8-й и 9-й вершин найдем число 5-й вершины: min(5+7, 5+8)=12. Ребро (5,8) изобразим двумя чертами со стрелкой.

По числам 9-й и 10-й вершин найдем число 6-й вершины: min(5+7, 4+3)=7. Ребро (6,10) изобразим двумя чертами со стрелкой.

По числам 9-й и 10-й вершин найдем число 7-й вершины: min(5+4, 4+6)=9. Ребро (7,9) изобразим двумя чертами со стрелкой.

По числу 5-й вершины определим число 2-й вершины: 12+7=19. Ребро (2,5) изобразим двумя чертами со стрелкой.

По числам 5-й, 6-й и 7-й вершин определим число 3-й вершины: min(12+2, 9+2, 7+6)=11. Ребро (3,7) изобразим двумя чертами со стрелкой.

По числам 6-й и 7-й вершин найдем число 4-й вершины: min(7+3, 9+8)=10. Ребро (4,6) изобразим двумя чертами со стрелкой.

По числам 2-й, 3-й и 7-й вершин определим число 1-й вершины: min(19+1, 11+5, 10+4)=14. Ребро (1,4) изобразим двумя чертами со стрелкой. Длина кратчайшего пути равна 14.

Двигаемся из начальной вершины 1 в конечную вершину 11 по ребрам со стрелкой. Получаем кратчайший путь 1-4-6-10-11. Его длина равна 14.

Задача.

1. Найти маршрут минимальной длины от пункта 1 к пункту 10.

Коммуникационная сеть минимальной длины – это совокупность дуг сети, имеющая минимальную суммарную длину и обеспечивающая связь между всеми узлами сети.

Алгоритм построения:

1. Начать с любого узла и соединить его с ближайшим узлом. Считаем, что это связанные узлы, а все другие – несвязанные.

2. Определить несвязанный узел, ближайший к одному из связанных узлов. Если их несколько, выбрать любой. Добавить этот узел к связанным. И так до тех пор, пока есть несвязанные узлы.

Пример. Университет устанавливает компьютерную систему электронной почты между деканатами.

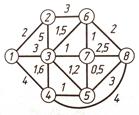
Протяженность коммуникаций в километрах отмечена на дугах. Необходимо установить связь, позволяющую восьми деканатам обеспечить доступ к системе при минимальной длине коммуникаций.

Начинаем с узла 1. Ближайший к нему узел – это узел 2 на расстоянии 2. Считаем, что узлы 1,2 – свзанные, и отметим это двойной чертой.

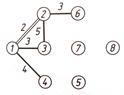
Ближайшие несвязанные узлы к одному из связанных узлов 1 и 2 – это узлы 3 и 6. Выбираем любой из них, например узел 3. Ребро 1-3 отметим двойной чертой и считаем узлы 1,2,3 связанными.

Далее ищем ближайший несвязанный узел к узлам 1,2,3,. И т.д.. В результате получим минимальное дерево.

Его длина равна сумме расстояний на дугах: 2+3+1+1+0,5+1+2=10,5 (км).

Задача.

Необходимо проложить сеть в районе для кабельного телевидения. Узлы сети показывают точки, к которым должна быть проложена кабельная сеть. Дуги отображают расстояние. Нужно предложить решение, которое позволит обеспечить доступ кабельной сети ко всем точкам, но при этом общая протяженность линий будет минимальной.

Дата добавления: 2014-11-29