Допуски угловых размеров

ИЗМЕРЕНИЕ УГЛОВ И КОНУСОВ

Контрольные вопросы к разделу 6

1. Что такое «оптическая система»?

2. Дайте определение линзе, окуляру, объективу.

3. Что такое «оптический рычаг»?

4. Какие приборы рассмотрены в данном разделе и что их объединяет?

5. Какие области применения имеют оптико-механические приборы?

6. Назначение, устройство и характеристика оптикатора.

7. В чем отличие оптикатора от микрокатора?

8. Как устроена трубка оптиметра с окуляром?

9. Как отсчитываются показания по трубке оптиметра с окуляром?

10. Какие основные узлы содержит оптиметр?

11. Как проверить перпендикулярность линии измерения к плоскости стола вертикального оптиметра?

12. Как настроить вертикальный оптиметр на нуль?

13. Выполните схему вертикального длиномера ИЗВ-1?

14. Какую цену деления имеет вертикальный длиномер и как выполняется отсчет показаний?

15. Как устроен спиральный нониус отсчетного микроскопа длиномера?

16. Какие типы микроскопов рассмотрены в данном разделе?

17. Нарисуйте оптическую схему инструментальных микроскопов?

18. Как устроен инструментальный микроскоп БМИ?

19. В чем отличие инструментальных микроскопов от универсального микроскопа УИМ-21?

20. Для каких измерений предназначены проекторы?

21. Какие существуют методы измерений и контроля на проекторах?

22. Перечислите основные узла универсального микроскопа УИМ-21

23. Как снимается отсчет по спиральному нониусу микроскопа?

24. Что означает «измерение в отраженном свете»?

25. Какие сменные окулярные головки на УИМ-21 Вы знаете?

26. Какое назначение имеет угломерная окулярная головка?

27. Назначение центровой бабки с делительной головкой на УИМ-21.

28. Какие измерения можно проводить на плоском столе?

29. Особенности круглого стола УИМ-21.

30. Для чего предназначена щуповая головка?

31. Как осуществляют измерения на микроскопах?

32. Как можно измерить диаметр вала на микроскопе?

33. Для каких измерений и контроля можно использовать микроскопы?

При конструировании машин наиболее часто используют нормальные углы, которые можно разделить на три группы:

1) нормальные углы общего назначения;

2) нормальные углы специального применения;

3) специальные углы, размеры которых связаны с расчетными зависимостями и которые нельзя округлить до нормальных углов.

Размеры углов первой группы приведены в табл. 7.1 и 7.2. Пример углов второй группы показан в табл. 7.3.

Таблица 7.1

Размеры и ряды нормальных углов общего назначения

Р я д
0^0	0^0   0^030¢   1^0   2^0   3^0	0^0 0^015¢ 0^030¢ 0^045 1^0 1^030¢ 2^0 2^030¢ 3^0 4^0	15^0	15^0   20^0	15^0 18^0 20^0 22^0 25^0	60^0	60^0 75^0	60^0 65^0 70^0 75^0 80^0 85^0
30^0	30^0	30^0 35^0 40^0	90^0	90^0	90^0 100^0 110^0
5^0	5^0 8^0	5^0 6^0 7^0 8^0 9^0 10^0 12^0	45^0	45^0	45^0 50^0 55^0	120^0	120^0	120^0 135^0 150^0 180^0 270^0 360^0
При выборе углов 1-й ряд следует предпочитать 2-му, 2-й — 3-му.

Таблица 7.2

Углы конусов и уклонов нормальных конусностей

d D С = 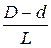= 2 tg a/2, где С – конусность; a – угол конуса; D – диаметр большого основания конуса; a / 2 – угол уклона; L d – диаметр малого основания конуса
Конус- ность	Угол конуса a	Угол уклона a/2	Конус- ность	Угол конуса a	Угол уклона a/2
Градус	Радиан	Градус	Радиан	Градус	Радиан	Градус	Радиан
1:200	17¢11,3²	0,00500	8¢35,6²	0,002500	1:7	8°10¢16	0,142615	4°5¢8	0,071307
1:100	34¢22,6²	0,010000	17¢11,3²	0,005000	1:5	11°25¢16	0,199337	5°42¢38	0,099669
1:50	1°8¢45	0,019990	34¢22,6²	0,010000	1:3	18°55¢28	0,330297	9°27¢44	0,165149
1:30	1°54¢34	0,033330	57¢17,5²1	0,016665	1:1,866	30°	0,523599	15°	0,261799
1:20	2°51¢51	0,049990	°25¢55	0,024995	1:1,207	45°	0,785398	22°30¢	0,392699
1:15	3°49¢5	0,066642	1°54¢32	0,033321	1:0,866	60°	1,047198	30°	0,523299
1:12	4°46¢18	0,083285	2°23¢9	0,041643	1:0,652	75°	1,308997	37°30¢	0,654498
1:10	5°43¢29	0,099915	2°51¢44	0,049957	1:0,500	90°	1,570796	45°	0,785398
1:8	7°9¢9	0,124838	3°34¢34	0,062419	1:0,289	120°	2,094395	60°	1,047198

Таблица 7.3

Углы конусов и уклонов конусностей специального назначения

Конус-	Угол конуса a	Угол уклона a2	Конус Морзе
ность	Градус	Радиан	Градус	Радиан	№	Диаметр, мм
1:19,212	2^058¢54²	0,052039	1°29¢27²	0,026020		9,045
1:20,047	2^051¢26²	0,049872	1°25¢43²	0,024936		12,065
1:20,020	2^051¢41²	0,049940	1°25¢50²	0,024970		17,780
1:19,922	2^052¢32²	0,050185	1°26¢16²	0,025093		23,825
1:19,254	2^058¢31²	0,051926	1°29¢16²	0,025963		31,267
1:19,002	3^000¢53²	0,052614	1°30¢27²	0,026307		44,399
1:19,180	2^059¢12²	0,052126	1°29¢36²	0,026063		63,348

Допуском угла 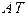(от англ. Angle Tolerance) называют разность между наибольшим 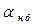и наименьшим 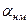предельными углами (рис.7.1). Допуски угловых размеров назначают по ГОСТу 8908 в зависимости от длины 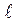меньшей стороны угла.

Допуск угла может выражаться:

1. в угловых единицах радианной и градусной мер 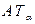(точное значение);

2. в округленном значении градусной меры ;

3. в линейных единицах 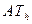- длиной противолежащего отрезка на перпендикуляре к стороне угла на расстоянии 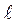от вершины (рис.7.1).

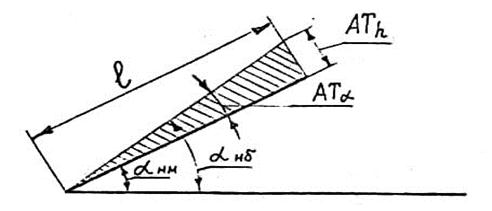
Рис. 7.1. Схема допуска угла

Связь между допусками в угловых и линейных единицах выражается следующей зависимостью:

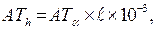(7.1)

где 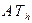- мкм; 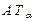- мкрад; 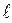- мм.

Напоминаем, что 1 мкрад (микрорадиан) = 10^-6 радиан. Соотношения между градусом и радианом следующие:

1° = 2p / 360 = 0,017453 рад = 17453 мкрад, (7.2)

1¢ = 0,00029088 рад» 291 мкрад; (7.3)

1рад = 360° / 2p = 57° 17¢ 44,8². (7.4)

При малых углах ( 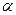< 10°) синус и тангенс угла практически равен величине угла, выраженного в радианах.

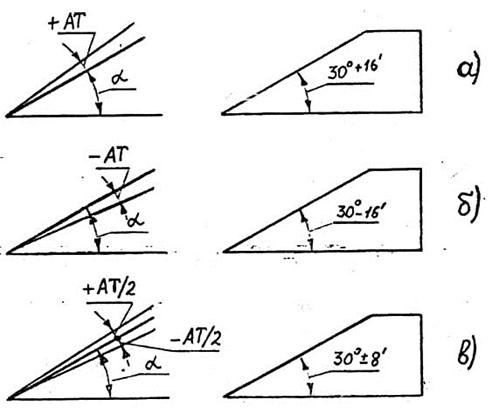
Применяют три типа расположения поля допуска относительно номинального угла (рис. 7.2): плюсовое (+ 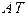), минусовое (- 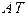) и симметричное (± 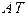/ 2). ГОСТ 8908 устанавливает 17 степеней точности для допусков углов: , ,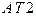..., . 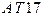Выборка из ГОСТа 8908 приведена в табл. 7.5 настоящего пособия.

+ АТ

а б в

30° + 16'

α

– АТ

30° – 16'

α

+ АТ /2

30°±8'

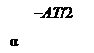Рис. 7.2. Схемы расположения полей допусков углов

Дата добавления: 2014-11-29