Зменшення впливу випадкових похибок

Опрацювання результатів прямих багаторазових вимірювань

Зазвичай процес одержання результату вимірювань не закінчується після відліку вимірюваної величини. Вимірювання параметрів складних процесів потребує опрацювання одержаних результатів.Під час опрацюван­ня результатів виконують два завдання – знаходять найкращу мето­дику опрацювання та оцінюють характеристики точності вимірювання. Результат вимірювання є повноцінним, якщо він супроводжується оцінкою його точності. Крім того, разом з результатом вимірювання доцільно вказати інші важливі дані, наприклад такі, як кількість спостережень (вимірювань) і їх статистичний розподіл, алгоритм опрацювання, характеристики вимірювальних засо­бів, умови вимірювань, способи корекції систематичних похибок, імовірнісні показники тощо. Наявність цих даних забезпечує можливість порівняння результатів вимірювань, виконаних однаковими чи різними методами, різними засобами, у різних уста­новах.

Обсяги опрацювання залежать від різновиду вимірювання, кількості експеримен­тальних даних, вимог щодо точності вимірювання, апріорної інформації про система­тичні та випадкові похибки вимірювання тощо. Лише при прямих разових вимірюван­нях отриманий результат спостереження може бути результатом вимірювання (якщо систематичні похибки вимірювання не коригують). В інших вимірюваннях опрацювання може здійснюватися за стандартизованими методиками (наприклад, статистич­ними методами), або потребувати створення спеціальних алгоритмів.

У загальному випадку опрацювання передбачає такі етапи:

- попередній аналіз результатів спостережень (вимірювань), їх систематизація, відкидання явно недостовірних результатів;

- корекція (зменшення) впливу систематичних похибок (вивчення умов вимірювань, розра­хунок і внесення поправок);

- аналіз впливу випадкових похибок, перевірка гіпотез про їх розподіл, вибір найкращих оцінок вимірюваних величин;

- оцінювання характеристик точності числового алгоритму, його стійкості;

- виконання розрахунків згідно з вибраним алгоритмом;

- аналіз отриманих результатів;

- подання результатів вимірювань та характеристик їх точності за відповідною формою.

Під час оцінки результатів вимірювань часто виходять із того, що вимірювання можна повторити багаторазово. Умови проведення вимірювань при цьому не повинні змінюватися.

Досвід показує, що будь-яке вимірювання, як би акуратно воно не здійснювалося, не може бути зовсім вільним від помилок або похибок.

Розглянемо, наприклад, результати експерименту (рис. 3.1), під час якого було виконано 100 незалежних вимірювань деякої фізичної величини в незмінних умовах. Видно, що при кожному окремому вимірюванні реєструється новий результат, відмінний від попереднього. Ця відмінність є причиною наявності випадкових помилок або випадкових похибок.

Результат вимірювання, х		0 50 100	хд
	Номер вимірювання, n

Рис. 3.1. Результати вимірювань деякої фізичної величини як функція номера вимірювання.

Випадкові похибки не можна виключити в кожному з результатів вимірювань, вони завжди будуть існувати. Однак за допомогою методів теорії імовірності можна врахувати їхній вплив на оцінку дійсного значення вимірюваної величини х_д.

Урахування впливу випадкових (статистичних) похибок ґрунтується на знанні законів їхнього розподілу, тому що випадкові похибки вимірювання характеризуються певним законом розподілу. Існування такого закону можна виявити, повторюючи вимірювання деякої величини багато разів у незмінних умовах.

Кожному результату вимірювань, який випадково відрізняється від істинного значення вимірюваної величини, відповідає певна ймовірність одержання цього результату Р.

Співвідношення, яке пов’язує можливі результати вимірювань з імовірностями їх одержання, називається законом розподілу цих результатів. На практиці під час оцінки випадкових похибок вимірювань використовують диференційну функцію розподілу (рис. 3.2).

Диференційну функцію розподілу р(х) часто називають щільністю ймовірностей (рис. 3.3), а її криву – кривою розподілу.

р(х)
	хд х

Рис. 3.2. Диференційна функція розподілу результатів вимірювань.

З рис. 3.2 видно, що диференційна функція розподілу результатів вимірювань має дзвоноподібну форму. Такий розподіл результатів вважається нормальним.

Якщо здійснити велику кількість вимірювань однієї й тієї самої величини при незмінних умовах, то переважна більшість результатів буде накопичуватися біля деякого результату, який, можливо, і є дійсним. Відносно цього можливого дійсного результату по обидва боки розташовані інші результати, причому чим далі від можливого дійсного результату вони розташовані, тим менше ймовірність їх одержання.

р(х)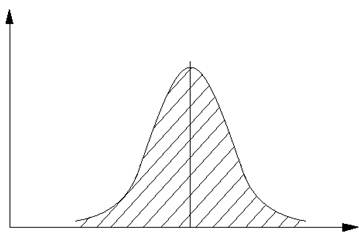
	хд х

Рис. 3.3. Щільність імовірностей одержання певного результату.

На рис. 3.1 показано результати вимірювань величини х як функцію номера вимірювання n. Видно, що вони сконцентровані поблизу деякої величини х_д. У переважній більшості випадків дійсне значення вимірюваної величини х_д, за умови нормального розподілу результатів, є середнім арифметичним усіх результатів вимірювань (середнім статистичним).

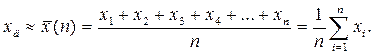(3.4)

Очевидно, що усереднена за n вимірюваннями величина буде набагато точніше характеризувати вимірювану величину, ніж результати окремих вимірювань.

Незважаючи на те, що в середньому всі результати вимірювань концентруються поблизу 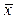, результати окремих вимірювань відрізняються від .

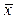Якщо вважати, що 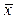– це найкраща оцінка величини х, то величина різниці 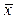і х називається похибкою (відхиленням) від середньої величини або Δ х:

Δ х = х – 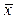. (3.5)

Якщо треба оцінити точність вимірювань і для цього спробувати одержати деяке усереднене значення похибки (обчислити середнє арифметичне з усіх похибок відносно 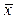), то усереднена величина дорівнюватиме нулю.

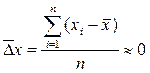. (3.6)

Щоб уникнути цього, у статистиці використовують іншу величину, яка дорівнює сумі квадратів відхилень кожного результату відносно середнього арифметичного, що називається дисперсією (розсіянням) і позначається символом D.

(3.7)

Дисперсія є мірою щільності групування значень похибки навколо очікуваного (середнього арифметичного) результату, мірою розсіювання випадкових похибок.

Слід зауважити, що величина дисперсії перевищує окремі значення похибок і тому вона незручна для використання. Для одержання середнього значення відхилень результатів вимірювань відносно середнього арифметичного добувають квадратний корінь з дисперсії. Одержане усереднене відхилення називається середнім квадратичним відхиленням (або стандартним відхиленням) σ_x:

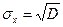. (3.8)

Середнє квадратичне відхилення σ_х характеризує середню похибку окремих вимірювань х₁, х₂,..., х_n, оскільки воно показує імовірність виявлення значень в інтервалі [ 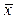– s_х, 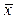+ s _х ].

Треба зазначити, що формули дисперсії та середнього квадратичного відхилення справедливі тоді, коли кількість вимірювань необмежено велика. На практиці ми маємо справу з обмеженою кількістю вимірювань (5...20). У такому випадку розподіл результатів відносно середнього арифметичного менший і несиметричний, виникає додаткова похибка вимірювань. Для штучного збільшення дисперсії формулу її визначення „модифікують” таким чином:

. (3.9)

Середнє квадратичне відхилення результатів вимірювань тоді має такий вигляд:

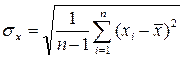. (3.10)

Однак треба пам’ятати, що ці формули справедливі при невеликій кількості вимірювань (не більше 20).

При збільшенні n розрахунки за співвідношеннями (3.7) і (3.9) приводять до практично однакових результатів.

Якщо кількість спостережень дуже велика, то піддана випадковим коливанням величина σ_х прагне досягти постійного значення σ:

. (3.11)

Квадрат цієї величини називається генеральною дисперсією вимірювань.

На жаль, ми не маємо можливості безліч разів вимірювати одну й ту саму величину, щоб отримати σ. На практиці вимірювання обмежені невеликою кількістю разів, за їх результатами завжди обчислюється не σ, а наближене до нього значення σ_х.

Усе сказане вище про похибки відноситься до похибок окремого вимірювання. Однак важливіше знати, наскільки може відхилятися від дійсного значення х середнє арифметичне 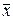, отримане для n повторних рівноточних вимірювань. Теорія свідчить, що середня квадратична похибка середнього арифметичного σ дорівнює середній квадратичній похибці окремого результату вимірювань σ_х, діленій на корінь квадратний із кількості вимірювань n, тобто

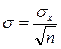. (3.12)

Нехай Р означає ймовірність того, що результат вимірювань відрізняється від дійсного на величину, не більшу, ніж Δ_х. Імовірність Р у цьому випадку називається довірчою імовірністю, а інтервал значень вимірюваної величини від – Δ_х до + Δ_х називається довірчим інтервалом.

Визначимо довірчий інтервал. Чим більшим буде даний інтервал, тим з більшою імовірністю х_д попадає в цей інтервал. З іншого боку, ширший інтервал дає меншу інформацію про величину х_д. Якщо обмежитися врахуванням тільки випадкових похибок, то при невеликій кількості вимірювань n для рівня довірчої ймовірності Р напівширина довірчого інтервалу дорівнює

, (3.13)

де t – коефіцієнт Стьюдента, значення якого наведені у Додатоку 1.

Наведена вище методика розрахунку похибок дає гарні результати (з надійністю 0,68) тільки в тому випадку, коли одна й та сама величина вимірювалася не менше, ніж 30-50 разів.

У 1908 році Стьюдент довів, що статистичний підхід справедливий також при малій кількості вимірювань. Розподіл Стьюдента при кількості вимірювань n → ∞ переходить у розподіл Гаусса.

Тому для розрахунку похибки за наведеною методикою було введено коефіцієнт Стьюдента, що залежить від Р та n.

У практиці вимірювань застосовуються різні закони розподілу випадкових похибок: трикутний, трапецієподібний, прямокутний, симетричний, нормальний. Однак найчастіше використовується закон розподілу Гаусса (нормальний). Він є граничним, до якого наближаються інші закони розподілу при типових умовах для вимірювання, тобто при

n → ∞. Теорією ймовірностей доводиться, що щільність імовірностей суми незалежних малих складових при необмеженому збільшенні їх кількості наближається до нормального закону розподілу незалежно від того, які закони розподілу мали ці складові. Найчастіше при вивченні випадкових похибок використовується закон їх нормального розподілу (рис. 3.4).

Довірчі межі випадкових похибок – це верхня та нижня межі інтервалу, в який похибки потрапляють із заданою ймовірністю Р (довірчою ймовірністю). Графічне зображення розташування довірчих меж при відомому середньому геометричному значенні σ наведено на рис. 3.5.

р(Δ)

–Δ_х 0 +Δ_х

Рис. 3.4. Крива та щільність розподілу випадкових похибок.

При нормальному розподілі похибок з імовірністю 0,68 випадкові похибки Δ_х знаходяться в довірчих межах ±1 σ; з імовірністю 0,95 – у межах ±2 σ; з імовірністю 0,9973 – у межах ±3 σ. Інакше кажучи, при нормальному розподілі 68 із 100 результатів вимірювань потраплять у межі середньої квадратичної похибки, у двічі більший інтервал потраплять 95 результатів, і майже всі результати (99,73%) будуть знаходитись у межах від – 3 σ до + 3 σ. Усі результати, що будуть одержані за межами 3 σ, імовірно є помилками.

р(Δ)

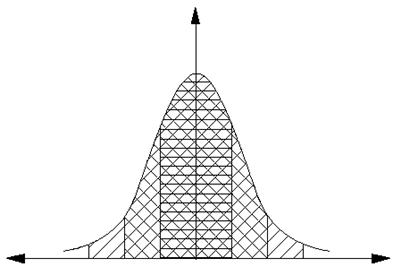
–Δ_х -3 σ -2 σ -σ 0 σ 2 σ 3 σ +Δ_х

Рис. 3.5. Довірчі межі та довірчі ймовірності при нормальному розподілі.

Для звичайних технічних вимірювань, коли не потрібен високий ступінь надійності та точності, довірча ймовірність береться в межах 2 σ, або 0,95.

Після знаходження коефіцієнта Стьюдента та розрахунку Δ _х ми маємо право стверджувати, що середній результат розрахунків із заданою ймовірністю Р знаходиться в інтервалі і відрізняється від дійсного значення на відносну величину

Якщо випадкова похибка виявилася завеликою, її можна зменшити підвищенням точності вимірювань або збільшенням кількості вимірювань n.

Крім випадкової складової похибки, у результатах вимірювання наявна систематична складова. Як правило, вважають, що всі заходи з усунення систематичної складової похибки були вжиті, проте в реальних умовах вона завжди наявна певною мірою. Систематичну складову похибки неможливо повністю усунути (компенсувати), але іноді досить важко її виявити. У будь-якому випадку є систематична складова похибки чи її немає – це ще треба довести.

Методика виявлення наявності систематичної складової похибки складається з таких дій:

1. Проводять дві серії вимірювань n₁ та n₂ однієї величини при незмінних умовах, але різними приладами і, якщо можливо, за різною методикою. Клас точності приладів для другої серії не повинен бути нижчий за клас точності для першої серії. Обчислюють середні арифметичні та .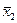

2. Визначають загальний розподіл похибок:

(3.14)

3. Обчислюють середнє квадратичне відхилення

(3.15)

4. Імовірність того, що різниця середніх арифметичних двох серій більша за відносну величину ε, або , визначається рівністю

. (3.16)

Імовірність Р знаходять з таблиці, що наведена у Додатку 1. за розрахованими t_p та n, де, відповідно, і n = n₁+ n₂ – 2.

Якщо Р ≥ 0,95, можна стверджувати, що наявна систематична похибка.

Зменшити систематичну похибку можна завдяки застосуванню більш точного обладнання, проаналізувавши та усунувши негативні зовнішні чинники, що впливають на процес вимірювання.

Вважається, що систематична похибка є припустимою, якщо вона зумовлена лише точністю вимірювального обладнання та становить не більше, ніж половину випадкової похибки.

Систематична похибка, як правило, зазначена в паспорті або на шкалі приладу, а в найпростіших випадках вона може бути прийнята рівною половині ціни поділки молодшого розряду шкали.

Сумарна похибка визначається як корінь квадратний із суми квадратів випадкової й систематичної похибок:

(3.17)

Дата добавления: 2014-11-29