Безразмерные коэффициенты для трапецеидальных законов движения

Безразмерные коэффициенты для законов движения с диаграммами ускорений из ветвей сопряженных гармоник и очерченных трапецией и вогнутой параболой

Для этих законов характерны следующие значения безразмерных коэффициентов пиков скорости, ускорения и динамической мощности.

Законы движения	Значения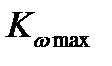
q	m	n	u
С диаграммой ускорений из двух ветвей сопряженных гармоник	0,03 0,05	– –	– –	– –	1,46 1,49	5,76 5,81	4,04 4,26
С диаграммой ускорений, очерченной трапецией и вогнутой параболой степени u	– – –	0,03 0,03 0,03	0,07 0,12 0,12	1,50 1,50 1,75	1,47 1,55 1,47	6,00 5,08 5,61	3,95 4,78 4,38

Диаграмма ускорении, очерченная трапецией и вогнутой параболой степени u, при u =1 превращается в трапецеидальную. Трапецеидальный закон движения характеризуется следующими показателями

Законы движения	Значения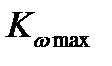
m	n
Трапецеидальный (неравнобокая трапеция)	0,05	0,10	1,62	5,40	4,40
0,05	0,20	1,71	4,88	5,46
0,05	0,30	1,83	4,57	6,80
Трапецеидальный (разнобокая трапеция)	0,05	0,40	2,00	4,44	8,40

Как видно из приведенных данных, применение при цикле выстой – перемещение – выстой последних двух законов движения, а также трапецеидального закона, является более целесообразным, чем применение синусоидального закона.

Для цикла выстой – прямой ход – обратный ход – выстой целесообразно применение комбинированного закона движения (рис. 11.12). В частях I и IV прямого и обратного ходов рекомендуется применить синусоидальный закон движения или лучше один из законов, представленных на рис. 11.11 с тем, чтобы обеспечить безударное начало и конец движения, а в частях II и III прямого и обратного ходов можно применить косинусоидальный закон. При этом угловое ускорение и угловая скорость должны представлять собой непрерывные функции. Условиями непрерывности функций и 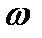являются: .

Рис. 11.12 Комбинированный закон движения для цикла выстой – прямой ход – обратный ход – выстой.

Эти условия легко выполняются при , поскольку в этом случае график углового ускорения для III и IV частей цикла комбинированного закона движения будет симметричен тому же графику для I и II частей цикла и, следовательно, достаточно будет удовлетворить первому условию, чтобы одновременно соблюдались остальные два условия.

Можно записать . Так как при равномерном вращении кулачка , где - угловая скорость кулачка, то, подставив значение в формулу для максимальной угловой скорости, получим .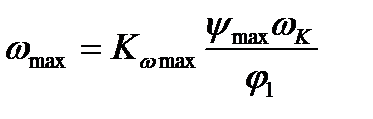

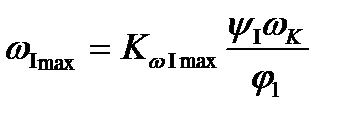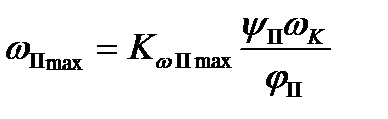Для I и II частей цикла комбинированного закона движения (рис. 12.13) получим: и . Учитывая условия непрерывности, . Учитывая также и , задаваясь 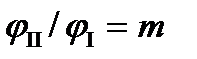, где - произвольное число, получим .

Тогда с учетом найденных значений значение 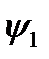будет равно .

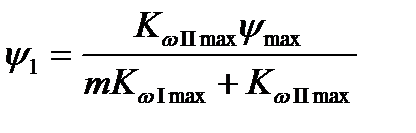Так как из заданной цикловой диаграммы механизма и выбранных для каждой части цикла законов движения величины известны, то можно найти 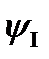, затем величину величины и .

Данные рекомендации для выбора закона движения при различных расчетных циклах движения толкателя относятся к кулачковым механизмам с геометрическим замыканием пары при учете только динамических нагрузок. Для каждого конкретного случая выбора закона движения нужно еще учитывать влияние игры толкателя, неизбежной при геометрическом замыкании. Если пара замыкается пружиной, то в части I прямого хода силы инерции и сила воздействия пружины имеют разные знаки, а в части II – одинаковые. Чтобы выровнять суммарные нагрузки, целесообразно повысить значение пика ускорения в части I и снизить в части II, уменьшив время и, соответственно, угол поворота, кулачка для части I прямого хода и увеличив время и угол поворота кулачка для части II прямого хода. Для части III обратного хода угол поворота кулачка должен быть соответственно увеличен, а для части IV – уменьшен.

Диаграммы ускорений для цикла выстой – перемещение – выстой при синусоидальном законе движения, для цикла прямой ход – обратный ход при косинусоидальном законе движения и для цикла выстой – прямой ход – обратный ход – выстой при комбинированном законе движения приведены на рис. 11.13 а, б, в.

Рис. 11.13 Диаграммы ускорений при пружинном замыкании кулачка и толкателя

Соотношения 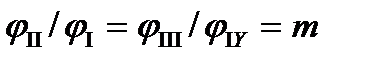принимаются в этом случае равными от 1,5 до 2,5. Наилучшее значение этого соотношения можно найти путем подсчета суммарных нагрузок от сил инерции и сил воздействия пружины.

Определение основных размеров кулачкового механизма. Основными расчетными размерами кулачкового механизма с качающимся толкателем (рис. 11.14) являются: радиус основного диска центрового профиля кулачка , длина толкателя l и межцентровое расстояние a.

Рис. 11.14 Схема кулачкового механизма с качающимся толкателем.

Острый угол 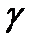между направлениями абсолютной и относительной скоростей точки A толкателя называется углом передачи движения. Острый угол 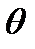между нормалью 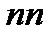к профилю кулачка и направлением абсолютной скорости 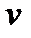точки A толкателя называется углом давления. Между углом передачи движения и углом давления, как видно из рисунка 11.14, существует определенная взаимосвязь .

Дата добавления: 2014-11-29