Основные уравнения. Реальная цепь, в которой возникает резонанс, содержит кроме катушки индуктивности и конденсатора активное сопротивление (рис

Реальная цепь, в которой возникает резонанс, содержит кроме катушки индуктивности и конденсатора активное сопротивление 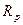(рис. 4.2).

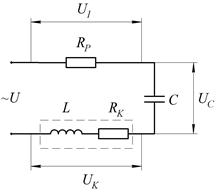
Рис. 4.2.

На основании 2-го закона Кирхгофа для цепи, изображенной на рис. 4.2 запишем:

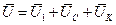(4.7)

а учитывая, что

, , ,

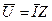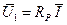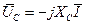имеем:

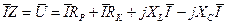(4.8)

Первые два члена выражения (4.8) представляют собой падения напряжений, совпадающие по фазе с током (падения напряжений на активных сопротивлениях)

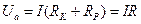(4.9)

где 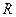- активное сопротивление всей цепи, два других члена - напряжения, отличающихся по фазе на 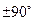от тока - реактивную составляющую напряжения

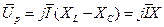(4.10)

где - реактивное сопротивление всей цепи. Подставим (4.9) и (4.10) в (4.8), получим

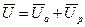
или переходя к мощностям

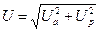(4.11)

а с учётом (4.8), (4.9), (4.10)

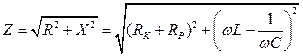(4.12)

Выражения, полученные ранее, позволяют записать значения 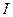, , 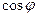, , , 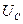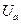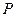через питающее напряжение и параметры цепи , , , .

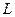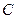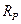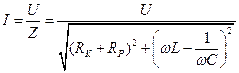(4.13)

(4.14)

(4.15)

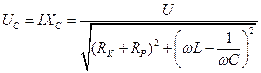(4.16)

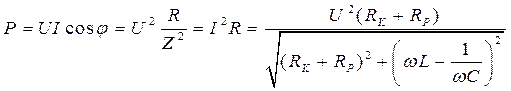(4.17)

При резонансе 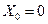(т. е. 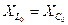) выражения для электрического состояния имеют следующий вид:

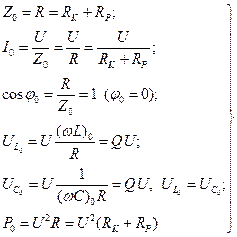
При резонансе цепь становится чисто активной (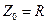, 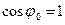), полное сопротивление цепи имеет минимальное значение, а ток максимальное. Напряжения на индуктивности и емкости равны и в добротность раз больше питающего (возбуждающего напряжения) напряжения. Активная мощность имеет максимальное значение ().

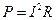Наступление резонанса в цепи нельзя определить с помощью условий резонанса (выражениями (4.2), (4.3), (4.4)) поскольку одна из величин этих выражений не измеряется, поэтому пользуются косвенными - максимум тока или активной мощности. Наиболее точный способ определения наличия резонанса в цепи - достижение фазового сдвига между напряжениями питания и током цепи равного 0. Однако он используется реже, поскольку необходим достаточно сложный прибор - фазометр.

Дата добавления: 2014-11-29