Коллекторные двигатели постоянного тока

Приводы

Поскольку в математических моделях ПИМ и ГИМ как объектов управления учтено действие соответственно пневмо- и гидроприводов, в дальнейшем рассматриваются только модели электроприводов (электрических машин) для ЭИМ с постоянной и переменной скоростью.

К приводам ЭИМ относятся:

- коллекторные двигатели постоянного тока (ДПТ);

- бесколлекторные двигатели постоянного тока (БДПТ);

- асинхронные трехфазные и однофазные двигатели (АД);

- синхронные трехфазные и однофазные двигатели (СД);

- шаговые двигатели (ШД).

К коллекторным двигателям постоянного тока или просто двигателям постоянного тока (ДПТ) относятся электрические машины, преобразующие электрическую энергию питающей сети переменного или постоянного тока в механическую энергию движения рабочих органов (РО) исполнительных механизмов (ИМ).

В системах автоматизации большинства технологических процессов и установок на основе ДПТ для регулирования координат и параметров технологического процесса применяются силовые пребразователи энергии (СПЭ) различного типа в зависимости от требований к электроприводу и его роли в АСУТП.

Ниже приведены математические модели коллекторных ДПТ в различных общепринятых в теории управления формах [6-10].

Электродвигатели постоянного тока (ДПТ) представляют собой объекты управления, регулируемые, в общем случае, по цепям якоря и возбуждения [11,12]. Применяются для регулирования скорости и положения рабочих органов как общепромышленных, так и специальных механизмов. Являются приводами ЭИМ с переменной скоростью. Функциональная схема и схемы замещения электродвигателя приведены на рис. 4.2.

Применяя декомпозицию ДПТ, нетрудно заметить, что в его структуре имеются три основных подсистемы или цепи (см. рис. 4.2б, 4.2в, 4.2г):

– цепь якоря, питаемая регулируемым напряжением U _я; R _э, L _э – соответственно эквивалентное активное сопротивление и эквивалентная индуктивность якорной обмотки; E _д – э.д.с. электродвигателя; i _я – ток якоря;

– цепь возбуждения, питаемая регулируемым напряжением U _в; R _в, L _в – соответственно эквивалентное активное сопротивление и эквивалентная индуктивность обмотки возбуждения; i _в – ток возбуждения;

– электромеханическая цепь, обеспечивающая преобразование электромагнитной энергии в энергию вращения вала ротора; J _д – момент инерции ротора электродвигателя; M, M _c – соответственно вращающий момент на валу электродвигателя и момент сопротивления на его валу; 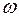- скорость вращения вала двигателя.

Рис. 4.2. Функциональная схема (а) и схемы замещения (б, в, г)

электродвигателя постоянного тока

Приведем описание ДПТ в различных формах, что позволит при необходимости легко установить взаимосвязь математических моделей.

Для описания динамических моделей электрических цепей электродвигателя (см. рис. 4.2) воспользуемся законами Кирхгофа, а для описания механической цепи – 2-м законом Ньютона. Тогда получим систему дифференциальных уравнений:

,

, (4.8)

,

где , 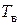– электромагнитные постоянные времени соответственно обмотки якоря и обмотки возбуждения, , .

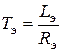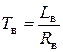Электромагнитные цепи двигателя взаимосвязаны. При подаче напряжения , по цепи якоря протекает ток 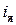, и при наличии магнитного потока создается электромагнитный момент, вращающий ротор,

, (4.9)

где 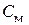– конструктивная постоянная двигателя.

Электромагнитные цепи и механическая цепь также взаимосвязаны, т.к. ток, протекающий по обмотке возбуждения, создает магнитный поток Ф, пронизывающий обмотку якоря и наводящий в ней э.д.с. вращения,

, (4.10)

где – конструктивная постоянная двигателя, в системе СИ равная по величине .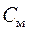

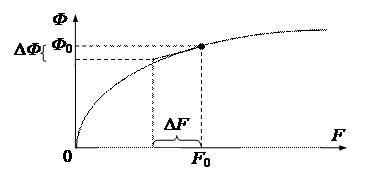Анализируя выражения (4.9), (4.10), заметим, что произведение переменных приводит к нелинейности математической модели электродвигателя, регулируемого одновременно по цепям якоря и возбуждения. Кроме того, при регулировании напряжения возбуждения двигателя проявляется нелинейный характер изменения потока Ф в функции тока возбуждения i _в (намагничивающей силы F = w _в i _в, где w _в – число витков обмотки возбуждения). Кривая намагничивания ДПТ соответствует нелинейному звену типа «насыщение» (рис. 4.3).

	А

Рис. 4.3. Кривая насыщения магнитной цепи ДПТ

Рабочая точка с координатами { F ₀, Ф ₀} на кривой насыщения соответствует некоторому, например номинальному режиму работы ДПТ.

ДПТ как нелинейный ОУ, регулируемый по цепям якоря и возбуждения, в соответствие с выражениями (4.8)…(4.10) и рис. 4.3 может быть представлен в виде структурной схемы (рис. 4.4).

Пусть электродвигатель регулируется только по цепи якоря (напряжение возбуждения 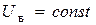, а, следовательно, и ). Тогда математическая модель электродвигателя примет вид

,

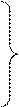
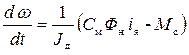. (4.11)

Рис. 4.4. Структурная схема ДПТ, регулируемого по цепям якоря

и возбуждения как нелинейного объекта управления

Математическая модель в виде (4.11) описывает ДПТ как линейный объект 2-го порядка.

Для перехода от дифференциальных уравнений (4.11) к операторным уравнениям произведем замену . Тогда получим

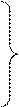
, (4.12)

.

По операторным уравнениям (4.12) составим структурную схему электродвигателя, приведенную на рис. 4.4.

Рис. 4.5. Структурная схема ДПТ, регулируемого по цепи якоря

Как видим, структурная схема ДПТ, регулируемого по цепи якоря, содержит 4 типовых линейных динамических звена: апериодическое, интегрирующее и 2 безынерционных звена, а также 2 суммирующих звена.

Пусть ДПТ регулируется одновременно по цепи якоря и возбуждения, причем изменения аддитивных (управляющих и возмущающих) воздействий незначительны или, по крайней мере, непрерывны. Тогда нелинейную модель ДПТ целесообразно линеаризовать в окрестности вектора рабочих траекторий и представить в виде линейной модели. В качестве рабочих траекторий примем уравнения M ₀ = C_м Ф ₀ i _я0, E _д = C_е Ф ₀ ω ₀, а все переменные ДПТ будем рассматривать в приращениях, т.е. в малой окрестности рабочих траекторий и обозначать через символ приращения ∆. Проведем также касательную линеаризацию кривой намагничивания, задавшись координатами { F ₀, Ф ₀} текущей рабочей точки и соответствующими приращениями (см. рис. 4.3).

Тогда математическую модель ДПТ можно представить системой уравнений в приращениях

,

(4.13)

,

,

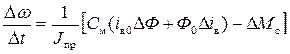где 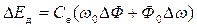, 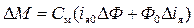– приращения координат э.д.с. двигателя и электромагнитного момента вдоль вектора рабочих траекторий;

– приращение магнитного потока;

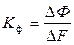– коэффициент линеаризации кривой насыщения магнитной цепи, являющийся функцией координат рабочей точки (см. рис. 4.3).

Структурная схема ДПТ, соответствующая уравнениям (4.13), приведена на рис. 4.6.

Приведем векторно-матричное описание ДПТ как объекта регулирования по цепи якоря, т.е. будем полагать, что напряжение возбуждения 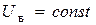, а магнитный поток .

Воспользуемся векторно-матричной моделью [10] линейных САУ в виде

, (4.14)

где – векторы соответственно состояния, управления и возмущения САУ,

, ; ,

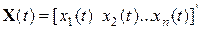– символ транспонирования;

Рис. 4.6. Структурная схема линеаризованного ДПТ как объекта

управления, регулируемого по цепям якоря и возбуждения

– стационарные матрицы соответственно состояния, управления и возмущения,

, ,

.

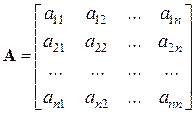Зададимся векторами состояния, управления и возмущения в виде:

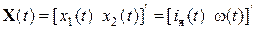l; 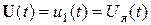; (4.15) .

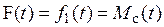По уравнениям (4.14), (4.15) найдем матрицы состояния, управления и возмущения:

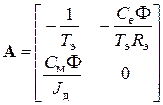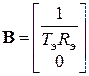; ; . (4.16)

Дата добавления: 2014-11-29