Интервальный ряд распределения

Во многих случаях, кота статистическая совокупность включает большое или тем более бесконечное число вариант, что чаще всего встречается при непрерывной вариации, практически невозможно и нецелесообразно формировать группу единиц для каждой варианты. В таких случаях объединение статистических единиц в группы возможно лишь на базе интервала, т.е. такой группы, которая имеет определенные пределы значений варьирующего признака. Эти пределы обозначаются двумя числами, указывающими верхнюю и нижнюю границы каждой группы. Применение интервалов приводит к формированию интервального ряда распределения.

Интервальный рад - это вариационный ряд, варианты которого представлены в виде интервалов.

Интервальный ряд может формироваться с равными инеравными ин­тервалами, при этом выбор принципа построения этого ряда зависит главным образом от степени представительности и удобности статистической совокупности. Если совокупность достаточно велика (представительна) по числу единиц и вполне однородна по своему составу, то в основу формирования интервального ряда целесообразно положить равенства интервалов. Обычно по этому принципу образуют интервальный ряд по тем совокупностям, где размах вариации сравнительно невелик, т.е. максимальная и минимальная варианты различаются между собой обычно в несколько раз. При этом величина равных интервалов рассчитывается отношением размаха вариации признака к заданному числу образуемых интервалов. Для определения равного и нтервала может быть ииспользована формула Стерджесса (обычно при небольшой вариации интервальных признаков и большом числе единиц в статистической совокупности):

(5.1)

где х_i - величина равного интервала; X max, X min— максимальная и минимальная варианты в статистической совокупности; n. — число единиц в совокупности.

Пример. Целесообразно рассчитать размер равного интервала по плотности радиоактивного загрязнения цезием – 137 в 100 населенных пунктах Краснопольского района Могилевской области, если известно, что начальная (минимальная) варианта равна I км/км², конечная ( максимальная) - 65 ки/км². Воспользовавшись формулой 5.1. получим:

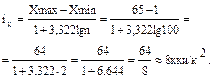
Следовательно, чтобы сформировать интервальный ряд с равными интервалами по плотности загрязнения цезием - 137 населенных пунктов Краснопольского района, размер равного интервала может составить 8 ки/км².

В условиях неравномерного распределения т.е. когда максимальная иминимальная варианты сотни раз, при формировании интервального ряда можно применить принцип неравных интервалов. Неравные интервалы обычно увеличиваются по мере перехода к большим значениям признака.

По форме интервалы могут быть закрытыми и открытыми. Закрытыми принято называть интервалы, у которых обозначены как нижняя, так и верхняя границы. Открытые интервалы имеют только одну границу: в первом интервале – верхняя, в последнем — нижняя граница.

Оценку интервальных рядов, особенно с неравным интервалами, целесообразно проводить с учетом плотности распределения, простейшим способом расчета которого является отношение локальной частоты (или частости) к размеру интервала.

Для практического формирования интервального ряда можно воспользоваться макетом табл. 5.3.

Т а б л и ц а 5.3. Порядок формирования интервального ряда населённых пунктов Краснопольского района по плотности радиоактивного загрязнения цезием –137

№ интервала	Интервалы по плотности загрязнения, ки/км^2	Частотные знаки	Локальные частоты	Накопленные частоты	Срединные значения интервала	Плотность распределения
			fл	fн	x	П
	1-9,0	/////			5,0	0,625
	9,1-17,0	///////////			13,0	1,375
	17,1-25,0	//////////////			21,0	1,750
	25,1-33,0	/////////////////////			29,0	2,625
	33,1-41,0	//////////////////////			37,0	2,750
	41,1-49,0	///////////////			45,0	1,875
	49,1-57,0	////////			53,0	1,000
	57,1-65,0	////			61,0	0,500
Итого	-		-	-	-

Основное преимущество интервального ряда — его предельная компактность. в то же время в интервальном ряду распределения индивидуальные варианты признака скрыты в соответствующих интервалах

При графическом изображении интервального ряда в системе прямоугольных координат на оси абсцисс откладывают верхние границы интервалов, на ос ординат — локальные частоты ряда. Графическое построение интервального ряда отличается от построения полигона распределения тем, что каждый интервал имеет нижнюю и верхнею границы, а одному какому- либо значению ординаты соответствуют две абсциссы. Поэтому на графике интервального ряда отмечается не точка, как в полигоне, а линия, соединяющая две точку. Эти горизонтальные линии соединяются друг с другом вертикальными линиями и получается фигура ступенчатого многоугольника, который принято называть гистограммой распределения (рис.5.3).

При графическом построении интервального ряда по достаточно большой статистической совокупности гистограмма приближается к симметричной форме распределения. В тех же случаях, где статистическая совокупность невелика, как правило, формируется асимметричная гистограмма.

В некоторых случаях имеется целесообразность в формировании ряда накопленных частот, т.е. кумулятивного ряда. Кумулятивный ряд можно образовать на основе дискретного либо интервального ряда распределения. При графическом изображении кумулятивного ряда в системе прямоугольных координат на оси абсцисс откладывают вариан­ты, на оси ординат — накопленные частоты (частости). Полученную при этом кривую линию принято называть кумулятой распределения (рис.5.4).

Формирование и графическое изображение различных видов вариационных рядов способствует упрощенному расчету основных статистических характеристик, которые подробно рассматриваются в теме 6, помогает лучше понять сущность законов распределения статистической совокупности. Анализ вариационного ряда приобретает особенное значение в тех случаях, когда необходимо выявить и проследить зависимость между вариантами и частотами (частостями). Эта зависимость проявляется в том, что число случаев, приходящихся на каждую варианту, определенным образом связано с величиной этой варианты, т.е. с возрастанием значений варьирующего признака частоты (частости) этих значений испытывают определенные, систематические изменения. Это означает, что числа в столбце частот (частостей) подвержены не хаотическим колебаниям, а изменяются в определенном направлении, в определенном порядке и последовательности.

Если частоты в своих изменениях обнаруживают определенную систематичность, то это означает, что мы находимся на пути к выявлению закономерности. Система, порядок, последовательность в изменении частот - это отражение общих причин, общих условий, характерных для всей совокупности.

Не следует считать, что закономерность распределения всегда дается в готовом виде. Встречается довольно много вариационных рядов, в которых частоты причудливо скачут, то возрастая, то уменьшаясь. В таких случаях целесообразно выяснить, с каким распределением имеет дело исследователь: то ли этому распределению вовсе не присущи закономерности, то его характер еще не выявлен: Первый случай встречается редко, второй же, второй же случай - явление довольно частое и весьма распространенное.

Так, при формировании интервального ряда общее число статистических единиц может быть небольшим, и в каждый интервал попадает малое число вариант (например, 1-3 единицы). В таких случаях рассчитывать на проявление какой-либо закономерности не приходится. Для того чтобы на основе случайных наблюдений получился закономерный результат, необходимо вступление в силу закона больших чисел, т.е. чтобы на каждый интервал приходилось бы не несколько, а десятки и сотни статистических единиц. С этой целью надо стараться, по возможности увеличивать число наблюдений. Это самый верный способ обнаружения закономерности в массовых процессах. Если же не представляется реальная возможность увеличить число наблюдений, то выявление закономерности может быть достигнуто уменьшением числа интервалов в ряду распределения. Уменьшая число интервалов в вариационном ряду, тем самым увеличивается численность частот в каждом интервале. Это означает, что случайные колебания каждой статистической единицы накладываются друг на друга, "сглаживается", превращаясь в закономерность.

Формирование и построение вариационных рядов позволяет получить лишь общую, приближенную картину распределения статистической совокупности. Например, гистограмма лишь в грубой форме выражает зависимость между значениями признака и его частотами (частостями) Поэтому вариационные ряды по существу являются лишь основой для дальнейшего, углубленного изучения внутренней закономерности статического распределения.

КОНТРОЛЬНЫЕ ВОПРОСЫ К ТЕМЕ 5

1. Что представляет собой вариация? Чем вызывается вариация признака в статистической совокупности?

2. Какие виды варьирующих признаков могут иметь место в статистике?

3. Что такое вариационный ряд? Какие могут быть виды вариационных рядов?

4. Что представляет собой ранжированный ряд? Какие его преимущества и недостатки?

5. Что такое дискретный ряд и какие его преимущества и недостатки?

6. Каков порядок формирования интервального ряда, какие его преимущества и недостатки?

7. Что представляет собой графическое изображение ранжированного, дискретного, интервального рядов распределения?

8. Что такое кумулята распределения и что она характеризует?

Дата добавления: 2014-11-29