Средняя квадратическая величина

При условии постановки значения К=2 в формулу 6.2. получаем среднюю квадратическую величину. В ранжированном ряду средняя квадратическая величина рассчитывается по невзвешенной (простой) форме:

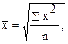(6.7)

где х – варианты ранжированного ряда; n – общее число вариант.

Порядок расчёта средней квадратической простой величины заключается в следующем:

1. Каждая варианта ранжированного ряда возводится в квадрат (Х²).

2. Полученные квадраты вариант суммируются (Σ х²).

3. Сумму квадратов делят на общее число вариант в ранжированном ряду .

4. Из полученного результата извлекают квадратный корень , что и представляет собой среднюю квадратическую величину для ранжированного ряда распределения.

Взвешанная форма средней квадратической величины, которая используется для дискретного или интервального ряда, выражается следующим образом:

(6.8)

Для расчёта средней квадратической взвешенной величины применяется следующий порядок:

1. Все варианты ряда возводят в квадрат (х²).

2. Полученные квадраты взвешивают по соответствующим им частотам (частостям) – (х²f).

3. Взвешенные квадраты суммируют (Σх²f).

4. Суммируют общее число вариант (Σf).

5. Сумму взвешенных квадратов делят на общее число вариант .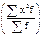

6. Из полученного результата извлекают квадратный корен 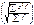, что представляет собой среднюю квадратическую взвешеную величину.

Средняя квадратическая величина, как самостоятельный вид средних, имеет ограниченное применение. Допустим, имеющееся две нестандартные цилиндрические емкости для хранения нефтепродуктов с диаметрами оснований 2 и 5 м необходимо заменить двумя новыми, равными по объему емкостями, имеющими в основании одинаковый диаметр. При расчёте среднего диаметра оснований новых емкостей по способу средней арифметической простой величины, т.е. 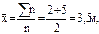полученный результат оказывается заниженным, и по этому диаметру объёмы новых емкостей будут меньше объемов имеющихся емкостей, что не соответствует условию задания. Дело в том, что площади оснований цилиндрических емкостей соотносятся между собой не линейно, а как квадраты их радиусов. Поэтому расчёт среднего диаметра новых емкостей целесообразно вести по средней квадратической простой величине:

Таким образом, диаметр оснований новых емкостей должен быть не 3,5, а 3,8 м.

Если же исходные данные представленных в виде дискретного или интервального ряда, то целесообразно применить способ средней квадратической взвешенной величины. Например, необходимо рассчитать средний диаметр сосновых брёвен по данным, приведённым в табл. 6.5.

Т а б л и ц а 6.5. Число и размер брёвен в штабеле

Число брёвен	Диаметр, см
в вершине	в комле

Из данных табл. 6.5 нетрудно убедится, что диаметр брёвен (варианта) представлен в виде интервального ряда, при этом число брёвен (частота) по каждой группе кратно 10. Это означает, что при расчёте среднего диаметра брёвен в штабеле выполняем по формуле 6.8. ход расчёта вспомогательных данных при определении среднего диаметра покажем в табл. 6.6.

Т а б л и ц а 6. 6. Порядок расчета среднего диаметра брёвен в штабеле

Число брёвен	Диаметр, см	Середина интервала, см	Квадраты диаметра	Взвешенные квадраты диаметра
Факт., шт	сокращенное	в вершине	в комле
f				x	X^2	X^2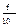
Σ 70		-	-	-	-

Целесообразно обратить внимание на то, что с учётом применения второго свойства средних величин конечный расчёт среднего диаметра брёвен в штабеле принимает следующий вид:

Таким образом, средневзвешенный диаметр сосновых брёвен в штабеле, рассчитанный по способу средней квадратической величины, составляет 46,5 см.

Главной сферой применение средней квадратической величины (в невзвешенной и взвешенной формах) является нахождение среднего квадратического отклонения, содержание и порядок расчета которого показан ниже в этой же теме.

Дата добавления: 2014-11-29