
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Уравнение множественной регрессии
|
|
|
|
Применение корреляционного метода при изучении зависимости признака – результата от нескольких факторных признаков формируется по схеме, аналогической простой (парной) корреляции.
Одной из важнейших задач многофакторного корреляционного комплекса является составление и решение уравнений множественной регрессии. Этот процесс включает следующие этапы: выбор уравнения взаимосвязи между признаками, отбор наиболее существенных факторных признаков, определение оптимального числа статистических единиц для получения несмещенных оценок.
При выборе формы корреляционной связи целесообразно учитывать следующие требования: во-первых, выбранное уравнение должно отражать основные черты закономерности, например, близкой к прямолинейной либо гиперболической или к параболической и т.п.; во-вторых, принятое аналитическое уравнение должно иметь по возможности несложный вид; в-третьих, число основных факторов должно быть рациональным.
Разработка множественной корреляционной модели всегда с отбором существенных факторов, оказывающих наибольшее влияние на признак-результат. При этом в задачу неоправданно большого числа факторов ведет к значительному усложнению ее решения. В то же время непродуманное исключение факторных признаков может привести к существенному искажению корреляционной взаимосвязи. В уравнение множественной регрессии не рекомендуется вводить те факторы, которые находятся между собой в тесной связи. В такой ситуации неизбежно явление коллениарности, т.е. корреляция между факторными признаками. Если несколько факторов коррелирует между собой, то может иметь место мультиколлениарности, т.е. зависимость между факторами множественной регрессии. Выявление мультиколлениарности проводится с помощью расчета парных корреляционных отношений или коэффициентов корреляции, отражающих меру тесноты связи между признаками-факторами. Условно принято, что если коэффициент корреляции превышает 0,8, то один из двух факторов выводится из системы.
Объективность результатов, получаемых при составлении и решении уравнений множественной регрессии, во многом определяется численность выборочной совокупности. Совершенно очевидно, что надежность корреляционных показателей зависит непосредственно от представительности выборки, так как сущность корреляционных расчетов базируется на использовании средних величин, надежность которых напрямую связана с числом единиц в совокупности. Поэтому разработка многофакторного корреляционного комплекса по малой выборке в социально-экономических явлениях имеет ограниченное применение в силу достоверности получаемых результатов. Для практической работы по составлению и решению многофакторной корреляционной модели принято считать, что численность выборки должна превышать число изучаемых признаков не менее, чем в 8 раз. Так, если для корреляционной модели отобрано, допустим, пять факторов, то в программе выборочного наблюдения необходимо предусмотреть не менее 40 (5-8) статистических единиц.
Стандартное уравнение множественной регрессии при условии включения n факторов можно представить в следующем виде:
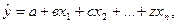 (11.24)
(11.24)
где 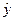 - среднее значение признака – результата, соответствующие заданным значениям факторных признаков х1, х2, ….., хn; а – среднее значение результата при условии полной изоляции влияния изучаемых факторов (х1, х2, ….., хn=0); в, с, …, z – неизвестные параметры, т.е. частные коэффициенты регрессии результативного признака при условии увеличения или каждого фактора на единицу.
- среднее значение признака – результата, соответствующие заданным значениям факторных признаков х1, х2, ….., хn; а – среднее значение результата при условии полной изоляции влияния изучаемых факторов (х1, х2, ….., хn=0); в, с, …, z – неизвестные параметры, т.е. частные коэффициенты регрессии результативного признака при условии увеличения или каждого фактора на единицу.
В качестве примера составим и решим уравнение регрессии, характеризующие зависимость годового объема механизированных работ на 1 условно эталонный трактор (признак-результат) от числа тракторов – машинистов, приходящихся на 100 га сельскохозяйственных угодий и на 1 физический трактор (признаки-факторы) по данным 100 сельскохозяйственных предприятий. Это означает, что необходимо составить и решить двухфакторный корреляционный комплекс, уравнение для которого в общем виде выглядит следующим образом:
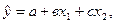 (11.25)
(11.25)
где 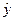 - средний годовой объем механизированных работ на 1 условный эталонный трактор; х1 – число трактористов –машинистов, приходящихся на 1 физический трактор; а, в, с – неизвестные параметры уравнения.
- средний годовой объем механизированных работ на 1 условный эталонный трактор; х1 – число трактористов –машинистов, приходящихся на 1 физический трактор; а, в, с – неизвестные параметры уравнения.
Для нахождения параметров а, в, с необходимо составить и решить систему нормальных уравнений, число которых равно количеству искомых параметров:
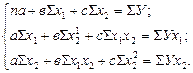
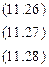
Из системы этих уравнений видно, что для определения параметров а, в, с необходимо рассчитать следующие значения: ΣХ1, ΣХ2, Σ У, Σ Х1Х2, Σ Х1 У, Σ Х2 У, Σ Х21, Σ Х22.
С этой целью приведем сокращенный вариант рабочей табл. 11.11.
Поставим полученные в табл. 11.11 конкретные значения 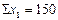 ;
; 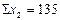 ;
; 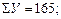
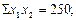
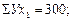
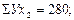
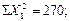
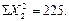
В уравнения 11.26 – 11.28. Получим
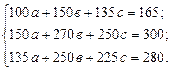
Разделим каждое полученное уравнение на коэффициент при а. Получим
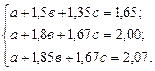
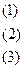
Вычитаем из уравнения 2 уравнение 1, а из уравнения 3 – уравнение 2; Получим
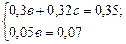
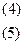
Из уравнения 5 находим параметр 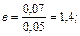
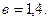
Теперь подставим рассчитанное значение параметра 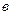 в уравнение 4. Получим 0,3 · 1,4+0,32 с=0,35; с=-0,22.
в уравнение 4. Получим 0,3 · 1,4+0,32 с=0,35; с=-0,22.
Для расчета параметра 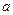 теперь уже известны параметры
теперь уже известны параметры 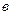 и с подставим, например, в уравнение 1. Получим а+1,5 · 1,4+1,35 · (0,22)=1,65; а=-0,15.
и с подставим, например, в уравнение 1. Получим а+1,5 · 1,4+1,35 · (0,22)=1,65; а=-0,15.
Т а б л и ц а 11.11. Расчет вспомогательных показателей для уравнения множественной регрессии
| № п.п. | Число трактористов-машинистов в расчете: | Годовой объем механизированных работ на 1 условный эталонный –трактор, тыс. га У | Расчеты величины | |||||
| На 100 га сельхозугодий Х1 | На 1 физический трактор Х2 | Х1Х2 | Х1У | Х2У | Х12 | Х22 | ||
| 0,8 | 0,7 | 0,8 | 0,56 | 0,64 | 0,56 | 0,64 | 0,49 | |
| 0,9 | 0,8 | 0,9 | 0,72 | 0,81 | 0,72 | 0,81 | 0,64 | |
| 1,0 | 1,0 | 1,0 | 1,00 | 1,00 | 1,00 | 1,00 | 1,00 | |
| … | .. | … | … | … | … | …. | … | … |
| 2,0 | 2,0 | 2,4 | 4,00 | 4,80 | 4,80 | 4,00 | 4,00 | |
| 2,1 | 2,0 | 2,4 | 4,20 | 5,04 | 4,80 | 4,41 | 4,00 | |
| 2,2 | 2,0 | 2,5 | 4,40 | 5,50 | 5,00 | 4,84 | 4,00 | |
| Σ |
Таким образом, конкретное уравнение, характеризующие влияние числа, приходящихся на 100 га сельхозугодий и на 1 физический трактор, на годовой объем механизированных работ, выполненных в расчете на 1 условный эталонный трактор, в 100 сельскохозяйственных предприятиях, приобретает следующий вид:
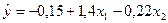 (11.29)
(11.29)
Параметр (коэффициент пропорциональности) 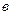 =1,4 показывает, что увеличение числа трактористов-машинистов на 1 человека в расчете на 100 га сельхозугодий способствует росту годового объема механизированных работ в среднем на 1,4 тыс. условных эталонных га. Параметр (коэффициент пропорциональности) с=-0,22 показывает, что увеличение на 1 тракториста-машиниста, приходящегося на 1 физический трактор, ведет к снижению годового объема механизированных работ в среднем на 0,22 тыс. условных эталонных га.
=1,4 показывает, что увеличение числа трактористов-машинистов на 1 человека в расчете на 100 га сельхозугодий способствует росту годового объема механизированных работ в среднем на 1,4 тыс. условных эталонных га. Параметр (коэффициент пропорциональности) с=-0,22 показывает, что увеличение на 1 тракториста-машиниста, приходящегося на 1 физический трактор, ведет к снижению годового объема механизированных работ в среднем на 0,22 тыс. условных эталонных га.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 409; Нарушение авторских прав?; Мы поможем в написании вашей работы!