
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм упорядочения графа
|
|
|
|
Целью введения порядковой функции на графе без контуров является разбиение множества вершин графа на непересекающиеся подмножества, упорядоченные так, что если вершина входит в подмножества с номером i, то следующая за ней вершина – в подмножество с номером большим i. Полученные непересекающиеся подмножества называются уровнями.
Алгоритм упорядочивания сводится к следующему:
1. В подмножество нулевого уровня 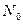 включаются все вершины i, у которых
включаются все вершины i, у которых  (i)=0 (пустое подмножество) (
(i)=0 (пустое подмножество) ( (i) определяет все вершины из которых можно непосредственно попасть в вершину i.) (множество левых инциденций). Производится последовательная нумерация вершин: 1,2… e.
(i) определяет все вершины из которых можно непосредственно попасть в вершину i.) (множество левых инциденций). Производится последовательная нумерация вершин: 1,2… e.
 (i)=0
(i)=0  (1)=0
(1)=0  (10)=0
(10)=0 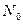 =
= 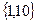
2. В подмножество первого уровня 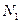 включаются все вершины i, у которых
включаются все вершины i, у которых
 (i)
(i) 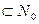 (подмножество
(подмножество  (i) включено в
(i) включено в 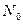 ).
).
Производится нумерация вершин e+1; e+2,…,  (9)=10
(9)=10  (8)=10
(8)=10  (5)=10
(5)=10 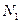 =
= 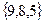
3. В подмножество второго уровня 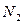 включаются все вершины i, у которых
включаются все вершины i, у которых
 (i)
(i) 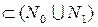
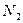 =
= 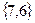
 (7)=(1,8,9)
(7)=(1,8,9)  (6)=(8).
(6)=(8).
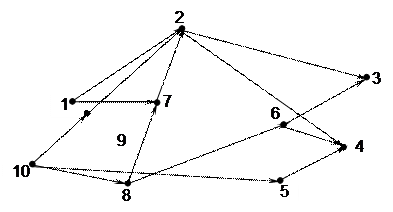 |
Рис. 3.3 Неупорядоченный граф.
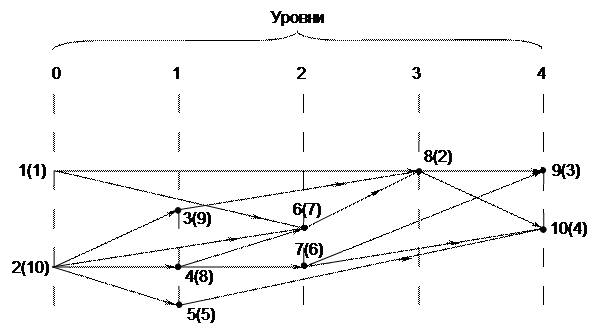 |
Рис.3.4. Упорядоченный граф.
4. В подмножество третьего уровня N3 включаются все вершины i, у которых
 (i)
(i)  (N0
(N0  N1
N1 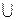 N2). N3={2}.
N2). N3={2}.  (2)={1,9,7}. Процесс продолжается до тех пор, пока не будут пронумерованы все вершины графа.
(2)={1,9,7}. Процесс продолжается до тех пор, пока не будут пронумерованы все вершины графа.
3.4. Числовая функция на графе. Алгоритм поиска критического пути.
Числовая функция на графе считается заданной, если каждой дуге (ai aj) ставится в соответствие число q=q(ai aj) из некоторого множества Q.
Значение функции на пути S через вершины а1, а2, …, аi, …., (аi 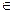 S) при задании числовой функции на дугах
S) при задании числовой функции на дугах
qs= 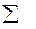 q(ai aj)
q(ai aj)
(ai aj) 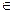 S
S
В соответствии с данным определением может быть поставлена задача нахождения путей через множество вершин с максимальным или минимальным значением числовой функции. Определение максимальных или минимальных путей на графе чаще всего формализуется в виде задачи динамического программирования в соответствии с функциональным уравнением Беллмана.
q 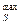 (ai aj)=max[q
(ai aj)=max[q 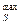 (ai aj)+q (ai aj)], ai
(ai aj)+q (ai aj)], ai 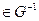 (aj), где q
(aj), где q 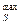 (ai aj)-максимальное значение целевой функции на путях S из некоторой начальной вершины а1 в вершину
(ai aj)-максимальное значение целевой функции на путях S из некоторой начальной вершины а1 в вершину
аj; q (ai aij)-значение функции на дуге (аi aj). При использовании данного уравнения считается, что все вершины в графе упорядочены. 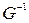 (aj) – множество левых инцинденций для вершин (aj)
(aj) – множество левых инцинденций для вершин (aj)
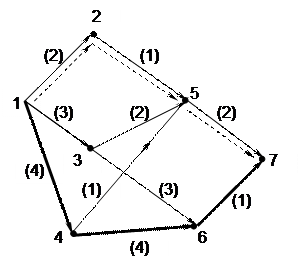
Пример. Найти max путь из вершины а1 в вершину а7. Принимаем для вершины а1
q 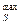 (a1 a1)=0. Для вершин а2, а3,
(a1 a1)=0. Для вершин а2, а3,  а4 : q
а4 : q 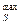 (a1 a2)=2; q
(a1 a2)=2; q 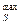 (a1 a3)=3; q
(a1 a3)=3; q 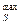 (a1 a4)=4.
(a1 a4)=4.
Для вершины а5: q 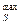 (a1 a5)=max (2+1; 3+2; 4+1)=5. Для вершины а6: q
(a1 a5)=max (2+1; 3+2; 4+1)=5. Для вершины а6: q 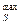 (a1 a6) = =max (3+3’; 4+4)=8. Для вершины а7: q
(a1 a6) = =max (3+3’; 4+4)=8. Для вершины а7: q 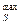 (a1 a7)=max (5+2; 8+1)=9.
(a1 a7)=max (5+2; 8+1)=9. 
Значение функции на max пути равно 9.
 |
Определение max и min путей имеет многочисленные приложения при проектировании информационно–управляющих систем: в задачах сетевого и календарного планирования для определения критического пути, в транспортных задачах, задачах контроля и технической диагностики.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1426; Нарушение авторских прав?; Мы поможем в написании вашей работы!