Топологическая декомпозиция структур

Описание потоков информации в системах управления.

Рассмотрим АСУП. Источник информации – документ. Взаимодействие

элементов в системе приводит к тому, что одни документы формируются на основании других, т.е. происходит движение информации с целью получения определённого функционального результата. Как для системы в целом, так и для любой подсистемы все документы могут быть классифицированы на:

1) исходные поступающие в систему;

2) внешние - результаты переработки исходных;

3) промежуточные – результаты переработки исходных, которые используются для вычисления внешних документов, но сами из системы не выдаются.

Совокупность исходных и внешних документов составляет информационный

базис системы. Между документами, входящими в поток, существуют отношения вхождения и порядка.

Отношение вхождения означает х_j=x_j1 x_j2 … x_jn, т.е. документ х_j образуется непосредственно из документов x_j1, x_j2, …x_jn, а отношение порядка: x_j следует за х_i – означает, что документ хj может быть образован только после документа х_i.

Если документам сопоставить вершины графа, а дугам соответствующие отношения вхождения и порядка, то получится структура, отражающая информационное взаимодействие элементов системы, и которая называется информационным графом.

Введение порядковой функции на этом графе позволит выявить его многоуровневую структуру и классифицировать документы по уровням формирования, т.е. упорядочить информационные процессы в АСУП.

Целью проведения топологической декомпозиции структуры СУ представленной в виде ориентированного графа является выделение в ней отдельных связаных подсистем. Для рассмотрения алгоритма декомпозиции введём понятие достижимого и контр достижимого множества вершин.

Множества вершин достижимых из вершины i называется достижимым множеством R(i):

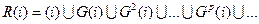
где G(i) - множество вершин, достижимых из вершины i с использованием путей, с длиной равной одной дуге. G^p(i) - множество вершин, достижимых из вершины i с использованием путей длинной p. При этом (i), сама вершина достижима с использованием пути длинной равной «0».

Контр достижимым множеством Q(i) графа системы G(V) называется множество таких вершин, когда из любой вершины этого множества можно достичь вершины i.

,

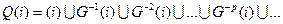где G^-Р(i) – множество вершин, из которых можно достигнуть i-й вершины, при этом длина пути равна р дугам, причем р = 0, 1, 2…

Операции выполняются до тех пор, пока множество существенных или неотъемлемых вершин, составляющее подсистемубудет:

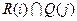
Множество 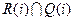содержит все существенные вершины и представляет или сильно сдвинутый подграф.

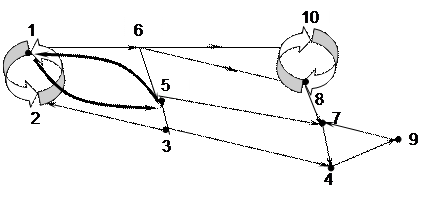
Рассмотрим пример:

Сильно связанный подграф для вершины 1: V₁

R(Ι)=(1,2,4,5,6,7,8,9,10) Q(Ι)=(1,2,3,5,6) V₁=(1,2,5,6);

Аналогично получим остальные связанные подграфы:

V₂=(3) V₃=(4,7,9) V₄=(8,10);

Дата добавления: 2014-11-29