Методы имитации случайных факторов при имитационном моделировании

Цели, порядок и схема имитационного моделирования.

Системный анализ объектов и процессов методом имитационного моделирования.

Имитационное моделирование является универсальным методом исследования сложных объектов и процессов. Этот метод заключается в том, что с помощью компьютера воспроизводится поведение исследуемого объекта или процесса, а исследователь – системный аналитик, управляя ходом процесса имитационного моделирования и, анализируя получаемые результаты, делает вывод о её свойствах и качестве поведения. Поэтому под имитационным моделированием следует понимать численный метод проведения на компьютере экспериментов с математическими моделями сложных объектов и процессов для определения интересующих исследователя функциональных характеристик.

Широкое применение метода имитационного моделирования в системном анализе обусловлено следующими причинами:

а) сложностью модели поведения системы; наличием множества случайных факторов, которые ограничивают эффективность применения традиционных аналитических методов исследования, а в ряде случаев вообще исключают возможность их применения, в результате чего имитационное моделирование оказывается единственно возможным способом исследования;

б) новыми возможностями, которые позволяют осуществлять: наблюдения за поведением системы в таких условиях, в которых натурный эксперимент просто невозможен (либо в силу чисто физических причин, либо в силу ограниченности временных и стоимостных ресурсов); проведения имитационных экспериментов в широком диапазоне изменения параметров системы и внешней среды, что позволяет получить дополнительную полезную информацию в условиях неопределённости всегда сопутствующей начальным этапам решения системных задач; прогнозирование поведения системы позволяет получить ответ в сжатом масштабе времени;

При имитационном моделировании можно выделить следующие основные этапы исследования:

1) Формулировка проблемы;

2) Построение математической модели функционирования системы;

3) Составление отладка компьютерной программы моделирования, включая разработку процедур моделирования различных случайных факторов;

4) Планирование имитационных экспериментов;

5) Проведение экспериментов и обработка результатов исследования.

Рассмотрим более подробно содержание каждого из этапов:

1. Формулировка проблемы.

Предполагает определения вопросов на которые надо ответить, либо гипотез которые надо проверить, либо воздействия которые надо оценить, что в целом определяет цель, имитации, в соответствие с которой должны быть определены и критерии, по которым оценивают результаты имитации.

2. Построение математической модели функционирования системы.

Включает в себя определения входных, выходных, управляющих переменных и их взаимосвязи в общем алгоритме функционирования системы с целью оценки значений выбранных критериев.

3. Составление машинной программы предполагает решение следующих задач:

а) составление самой программы с использованием, как универсальных алгоритмических языков, так и проблемно-ориентированных на решение задач имитации;

б) разработка программных процедур имитации различных случайных факторов, имеющихся в системе;

в) отладка программы.

4. При планировании экспериментов решаются следующие основные задачи:

а) выбор способов ускорения сходимости статистических оценок интересующих нас критериев к истинным значениям;

б) определение объёма имитационных экспериментов;

в) составление плана машинных экспериментов.

5. Проведение экспериментов и обработка результатов в основном преследуют цель: используя всё многообразие статистических критериев и максимум информации, полученной в процессе эксперимента, сделать выводы по результатам имитационного эксперимента и определить их точность.

В соответствии с вышеизложенным, общая схема имитационного моделирования имеет вид:

Рис. 6.1. Общая схема имитационного моделирования.

Обозначения: ГГР – генератор равномерно распределённых случайных чисел; П – преобразователь закона распределения; ФФ – формирующий фильтр; М – модель объекта или процесса; ИК – измерительный блок критерия функционирования объекта или процесса; БПЭ – блок планирования эксперимента; a - равномерно-распределённые случайные числа; x – случайные числа с заданным законом распределения; z – коррелированные случайные числа с заданной автокорреляционной функцией; y – случайные числа имитирующие выходную переменную объекта или процесса; U₁…U_k – управляемые переменные модели объекта или процесса; k - критерий функционирования моделируемого объекта или процесса.

Имитационный системный анализ поведения сложных объектов и процессов выполняется с учётом воздействий внешней среды. Возмущающие воздействия внешней среды являются, как правило, случайными процессами с характерными законами распределения и автокорреляционными функциями. При имитационном моделировании случайных факторов и возмущающих воздействий необходимо получить случайную последовательность чисел, имеющих такой же закон распределения и такую же автокорреляционную функцию, что и закон распределения и автокорреляционная функция реальных возмущающих воздействий. Базовой последовательностью случайных чисел для решения этой задачи является совокупность случайных чисел с равномерным законом распределения:

,

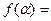
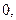
(6.1)

Псевдослучайные числа a можно получать программно, например с использованием формулы:

(6.2)

где обозначает выделение дробной части числа, полученного в скобках.

Последовательность чисел с нормальным законом распределения может быть получена в соответствии с выражением:

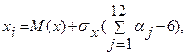(6.3)

где - математическое ожидание случайных чисел x; среднеквадратическое отклонение случайных чисел x; - равномерно распределённые случайные числа; 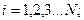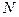- количество некоррелированных, случайных чисел с нормальным законом распределения.

Пусть автокорреляционная функция возмущающего воздействия имеет вид:

Рис. 6. 2. График автокорреляционной функции возмущающего воздействия.

Коррелированные случайные числа 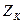получают в соответствии с выражением:

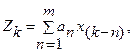(6.4)

где -номер коррелированного случайного числа; 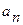- параметры формирующего фильтра; - количество коэффициентов.

Параметры формирующего фильтра находятся путём решения системы уравнений:

, (6.5)

где -значения автокорреляционной функции, которые берутся из графика (рис. 6. 2.).

Система уравнений (6. 5) решается методом Ньютона. Приближение корней системы уравнений (6. 5) выполняется в соответствии с реккурентным соотношением Ньютона:

(6.6)

где 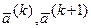- векторы к-го (к+1) приближения корней системы; 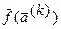- вектор, функция к-го приближения корней; 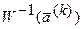- обратная матрица производных от вектор функции

Поиск вектора корней первого приближения выполняется в такой последовательности:

1. Задаются нулевым приближением корней то есть при К=0.

(6. 7)

2. Вычисляют значения вектор функции корней нулевого приближения:

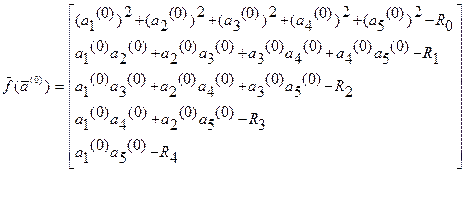(6. 8)

3. Вычисляют матрицу производных от вектор функции

(6. 9)

(6. 10)

С учётом (6. 9), получаем:

(6. 11)

В матрицу (6. 11) подставляют значения корней нулевого приближения и получим матрицу .

4. Обратную матрицу производных от вектор функции получают методом Гаусса.

5. Подставляют значения в формулу (6. 6) и находят вектор корней нулевого приближения.

Аналогично находят векторы корней первого, второго и последующих приближений параметров формирующего фильтра.

Приближение корней выполняют до тех пор, пока:

(6. 12)

где - заданная точность вычислений.

Имитация случайных чисел с любым, кроме нормального, законом распределения может быть выполнена методом обратных функций. Он основан на использовании следующей теоремы.

Если х случайная величина, равномерно распределённая на отрезке [0;1], то случайная величина y является решением уравнения

, (6. 13)

Имеет плотность распределения где - заданный закон распределения реакции возмущающего воздействия.

Таким образом последовательность чисел x₀, x₁, x₂,…, x_i преобразуется в последовательность чисел y₀, y₁, y₂,…, y_i имеющую заданную плотность распределения .

Пример: Необходимо получить последовательность чисел, имеющих распределения по показательной функции:

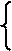
В соответствии с (6.13) имеем:

,

откуда

.

6.3. Определение объёма имитационных экспериментов.

Объём эксперимента – это число реализаций, которое необходимо провести при имитационном моделировании, чтобы обеспечить требуемую статистическую точность результатов. При определении объёма экспериментов обычно учитывают вид показателя эффективности.

Показателем эффективности может быть:

1) вероятность выполнения той или иной задачи;

2) некоторая скалярная функция параметров, алгоритма или структуры системы.

Рассмотрим первый случай. Пусть при имитационном моделировании исследуется вероятность появления события А, например отказ системы. Известно, что вероятность события А оценивается в процессе статистических испытаний как:

,

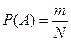где m – число случаев наступления события А при N реализациях.

В силу предельной теоремы теории вероятности:

, (6.15)

где - точность оценки; a - доверительная вероятность (a=0,95); t_a - квантиль нормального закона, соответствующий заданному значению a; d² – дисперсия часто-

ты ;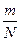

(6.16)

Из формул (6.15) – (6.16) получаем:

(6.17)

Рассмотрим второй случай. Оценка среднего значения показателя Е по множеству реализаций N определяется как:

, (6.18)

где Е_i – значения показателя эффективности в i-м эксперименте.

По центральной предельной теореме при большом N среднее арифметическое Е имеет распределение, близкое к нормальному с математическим ожиданием m_E и дисперсией 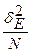, где d²_Е – дисперсия оцениваемой случайной величины. Поэтому, аналогично (6.15), имеем:

(6.19)

откуда: (6.20)

Дата добавления: 2014-11-29