На множник системи. Для аналізу впливу АР на множник системи зафіксуємо ФР

Для аналізу впливу АР на множник системи зафіксуємо ФР. Доцільно прийняти 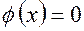, тобто розглядати синфазні системи (всі елементи антени збуджуються з однаковою початковою фазою).

Якщо 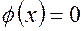, то вираз (6.16) набуває вигляд

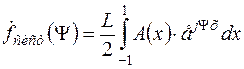. (6.17)

Розглянемо, особливості при різних законах АР.

Система з рівномірним амплітудним розподілом

Розглянемо синфазну систему з рівномірним АР, тобто систему, для якої (рис. 6.7, а). Це є найпростіші види амплітудного та фазового розподілів і антена з таким АФР є, свого роду, «еталоном», з яким порівнюють антени з іншими видами АФР. Для такої антени вираз (6.17) приймає вигляд

,

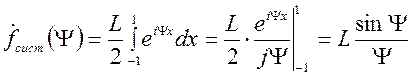а нормований множник системи

. (6.18)

Графік нормованого множника системи наведено на рис. 6.7, б.

Проведемо аналіз множника системи:

1) множник системи є симетричним відносно осі системи. Форма головного пелюстка подібна сплющенному тороїду, середина якого знаходиться посередині системи. Значення головного максимуму дорівнює довжині системи 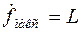. Напрямок головного максимуму визначається кутами

;

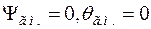2) напрямки нулів МС 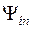визначаються значеннями кутів

; .

.

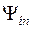
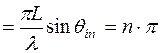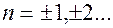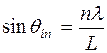3) напрямки максимумів бокових пелюсток наближено визначаються кутами, за яких функція |sinΨ| досягає максимумів, тобто

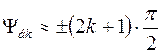, де . (6.19)

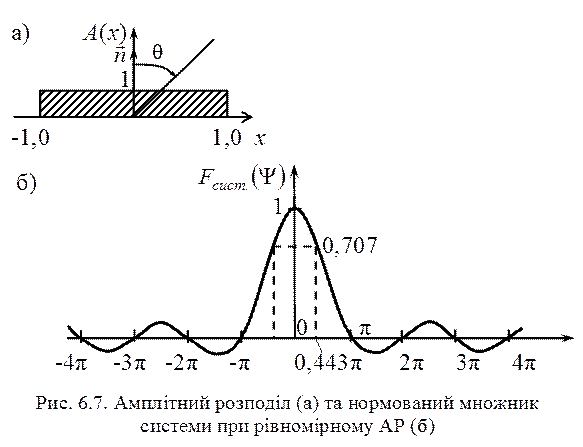
Узагальнені кутові координати перших трьох бокових пелюсток дорівнюють

.

Якщо підставити (6.19) у вираз (6.18), то отримаємо наближені значення рівня бічних пелюсток

.

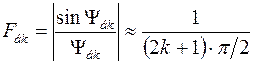Відповідно маємо

;

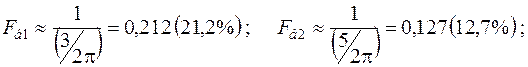
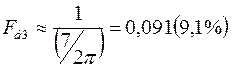4) ширина ДС за рівнем половинної потужності визначається шляхом рішення рівняння

.

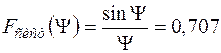Функція 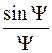дорівнює 0,707, якщо узагальнена кутова координата має значення

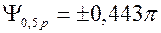або .

Зазвичай 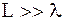, тобто система має велику спрямованість і синус малого кута, можна тоді замінити значенням кута в радіанах отримаємо повну ширину ДС

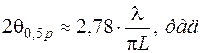або . (6.20)

Ширина ДС зворотно пропорційна електричній довжині системи ;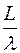

5) реальний кут змінюється у межах від 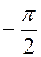до . Згідно цьому робоча область узагальнених кутів 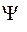(область видимості) визначається нерівністю

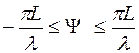. (6.67)

Ширина цієї області залежить від електричної довжини системи 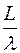. Оскільки система є синфазною робоча область розміщена симетрично відносно . Якщо 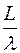=1, то в межах робочої області буде тільки головний пелюсток. Якщо 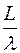=2, то з обох сторін від головного буде по одному боковому пелюстку. Якщо електрична довжина збільшується, то ширина ДС зменшується, а кількість бокових пелюсток зростає.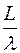

Коефіцієнт спрямованої дії системи можна визначити з виразу (5.23), якщо врахувати незалежність МС від координати 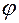, перейти до узагальненої координати та підставити (6.18), отримаємо

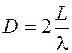. (6.21)

Очевидно, що коефіцієнт корисної дії антен з рівномірним АР дорівнює одиниці.

Недоліком антен з рівномірним АР є високий рівень бічних пелюсток ДС. Для їх зменшення використовують розподіл амплітуд, який спадає до країв антен.

Система з косинусоїдальним амплітудним розподілом

Косинусоїдальний АР описується рівнянням (рис. 6.8).

Тоді .

Після проведення інтегрування набудемо вираз

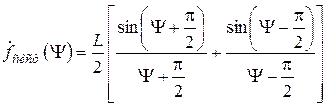. (6.22)

Максимальне значення досягається за умови 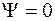і дорівнює 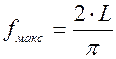.Відповідно, нормований множник буде мати вигляд

(6.23)

Якщо провести аналіз виразу (6.23) аналогічно аналізу для рівномірного амплітудного розподілу, то отримаємо:

1) ширина МС дорівнюватиме в узагальнених координатах

а в реальних 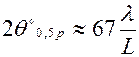; (6.23)

2) положення нулів визначається за умови 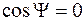, тоді маємо

3) максимуми бічних пелюсток розташовані приблизно посередині між нулями;

4) рівень бічних пелюсток дорівнює

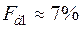або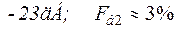

і порівняно з випадком рівномірного АР є невеликим.

КСД системи з косинусоїдальним АР дорівнює[]

.

КСД порівняно з випадком рівномірного АР зменшився на 19 %. Меншим буде і коефіцієнт використання довжини 0,81.

Система з частковим спаданням амплітуди

Розглянемо АР виду

(6.25)

де .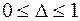

Значення 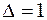відповідає рівномірному розподілу, значення – косиносоїдальному. За умови , то АР називають розподілом типу «косинус на п’єдисталі» (рис. 6.9).

Якщо підставити вираз (6.25) в (6.17), то можна отримати множник системи у вигляді

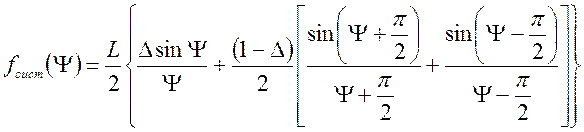. (6.26)

Максимальне значення множника системи в напрямі Ψ=0 дорівнює

.

Нормований множник має вигляд

.

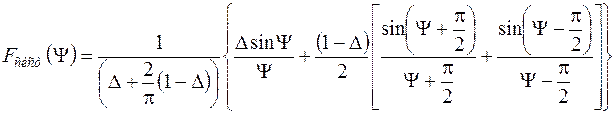Розглянемо випадок 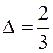. Нормований множник системи

. (6.27)

Для данного випадку параметри множника системи визначені в []:

а) ширина ДС

;

б) рівень перших двох бічних пелюсток

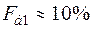або .

Якщо нормований множник системи (6.27) підставити (5.23), можна отримати

.

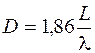Окрім розглянутих видів амплітудного розподілу на практиці можливі і інші типи розподілу, як симетричних 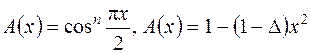, так і несиметричних, наприклад, експоненціальне .

Порівняльна характеристика впливу різних видів АР

Дата добавления: 2014-11-29