Коррекция характеристик АС

Понятие о коррекции. В автоматических системах, которые состоят только из основных функционально необходимых элементов, обычно не удается получить требуемые показатели качества регулирования. Это объясняется тем, что требования, предъявляемые к характеристикам системы, чаще всего носят противоречивый характер. Например, повышение точности системы в установившемся режиме требует повышать коэффициент усиления системы, но это мероприятие всегда уменьшает запас устойчивости системы и ухудшает переходный процесс. При этом система может стать неустойчивой раньше, чем удастся получить требуемый коэффициент усиления.

Покажем это на примере автоматической системы, у которой передаточная функция в разомкнутом состоянии имеет вид

. (8.13)

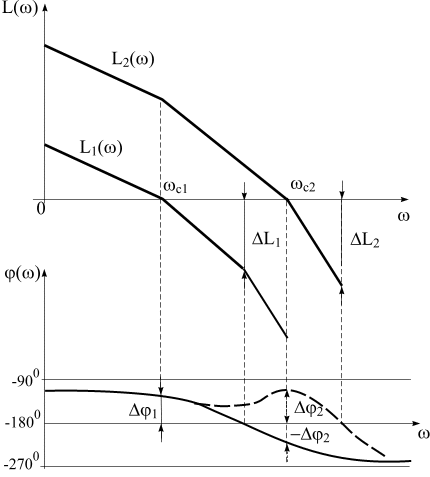
Приведенные на рис.8.4 логарифмические характеристики и 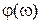этой системы показывают, что при коэффициенте усиления система имеет достаточный запас устойчивости по амплитуде 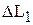и по фазе 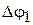, а, следовательно, и хороший переходный процесс. Но предположим, что при значении не обеспечивается заданная точность и для ее повышения требуется увеличить коэффициент усиления до значения 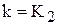. Как видно из графиков при этом коэффициенте усиления система стала неустойчивой. Это вызвано следующими физическими причинами.

С увеличением коэффициента усиления увеличивается частота среза системы 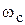и одновременно уменьшается запас устойчивости по фазе . Причиной этого является наличие в системе инерционных звеньев, которые вносят запаздывание по фазе. С увеличением частоты это запаздывание растет. Отсюда следует, что для сохранения устойчивости системы при увеличении ее коэффициента усиления надо компенсировать запаздывание в полосе частот вблизи частоты среза .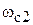

Это можно сделать коррекцией динамических характеристик системы, например, приподнять вверх ФЧХ так, как это показано на рис. 8.4 пунктирной линией. Если это удастся сделать, будет достигнута и необходимая точность и система сохранит необходимый запас устойчивости, который определится отрезками и .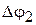

Рис.8.4. Логарифмические частотные характеристики системы с передаточной функцией по (8.13) при коэффициентах усиления и ().

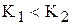Средства коррекции динамических характеристик. Коррекция осуществляется с помощью специальных корректирующих устройств, для которых подбирается определенный алгоритм обработки сигнала и схема включения устройства в систему.

Основными алгоритмами корректирующих устройств являются дифференцирующие, интегрирующие и интегро-дифференцирующие. В ряде случаев используются алгоритмы безынерционных и инерционных звеньев. Используются также различные сочетания этих алгоритмов.

Схемы включения корректирующих устройств делятся на последовательные, параллельные и комбинированные.

Последовательные корректирующие устройства обычно включаются после элемента сравнения в цепь основных воздействий и служат для преобразования отклонения (сигнала ошибки). В этом случае корректирующее устройство формирует выходной сигнал, представляющий собой производную или интеграл от входного сигнала по времени. К достоинствам последовательных корректирующих устройств относится простота их исполнения (в виде пассивных R-С контуров), а к недостаткам - высокая чувствительность к помехам, накладывающимся на основной сигнал. Введение в цепь основных воздействий последовательных корректирующих устройств в виде пассивных контуров часто сопряжено с ослаблением основного сигнала.

Параллельные корректирующие устройства образуют гибкую обратную связь по отношению к охваченной части структурной схемы. Они в некоторых случаях требуют применения специальных средств для своего осуществления, например тахогенераторов, стабилизирующих трансформаторов и др., и могут выполняться в виде простых однозвенных или многозвенных R-С контуров. К преимуществам параллельных корректирующих устройств относятся большая независимость динамических свойств скорректированной системы от изменения ее параметров, меньшая подверженность влиянию помех и др.

Пример. Корректирующие свойства дифференцирующей цепи. Здесь рассматриваются корректирующие свойства одной из распространенных дифференцирующих схем (рис. 8.5,а). Передаточная функция этой схемы

, (8.14)

где - коэффициент усиления цеп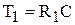и; и 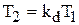- постоянные времени, характеризующие соответственно опережение и отставание. Поскольку 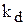<1, то .

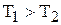АФЧХ рассматриваемой схемы является полуокружностью расположенной в первом квадранте (рис. 8.5,б). ЛАЧХ показана на рис. 8.5,в ломаной . ФЧХ в соответствии с формулой (8.14) определяется выражением

. (8.15)

и показана на рис. 8.5,в. Из последнего выражения видно, что числитель передаточной функции обуславливает опережение на угол 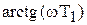, а знаменатель запаздывание на угол .

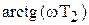Рис.8.5. Схема дифференцирующей фазоопережающей R-C цепи

и ее частотные характеристики

Так как для этой дифференцирующей схемы всегда 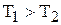, то она при всех частотах будет создавать опережение. Однако это опережение ощутимо только в определенной полосе частот, и существует частота при которой опережение максимально. Значение этой частоты определяется из условия 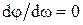и равно

.

Угол опережения на этой частоте равен

,

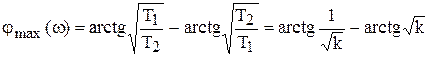и данная формула показывает, что максимальное опережение не зависит от абсолютных значений T₁ и T₂, а только от их отношения, или показывает, что получение больших углов опережения связано с уменьшением коэффициента усиления цепи.

Физическая трактовка процессов при введении производной в законе регулирования. Предположим, что сигнал рассогласования системы 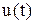и его производная 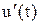изменяются по кривым, показанным на рис.8.6.

Если система реагирует только на сигнал рассогласования 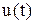, то при прохождении его через инерционные элементы исполнительный двигатель начнет его отрабатывать не сразу, а через некоторое время. Если же на исполнительный двигатель поступит сигнал пропорциональный не только сигналу рассогласования, но и его производной, то он начнет отрабатывать ошибку значительно раньше и интенсивнее. Второй существенный фактор в том, что в системе реагирующей только на сигнал 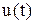вращающий момент двигателя одинаков, как в момент времени t₁, когда сигнал растет, так и в момент t₂, когда он убывает. Между тем желательно иметь другой алгоритм реакции, чтобы в момент t₁ усилие двигателя было бы больше для эффективного гашения ошибки, а в момент t₂ наоборот меньшее, чтобы предотвратить перерегулирование. Как следует из рис. 8.6 такой благоприятный алгоритм как раз и создается посредством дифференцирования сигнала.

ГЛАВА 9

Дата добавления: 2014-11-29