Статическая модель САР

Составление математических моделей САР

Общие замечания. Математические модели САР являются алгоритмичес­кой основой их проектирования. На их основе производится синтез систем, анализ их характеристик, расчет параметров настроек и т.д.

Процесс составления моделей можно разделить на два этапа: сначала пи­шут модель каждого элемента системы, затем составляется общая модель си­стемы в соответствии со схемой прохождения в ней сигналов. Существует достаточно много форм записи линейных математических моделей, но наибо­лее распространенными из них является запись в виде систем уравнений, струк­турных схем и передаточных функций.

Статическая модель описывает систему в установившемся режиме и по­этому используется для расчета параметров настройки ее элементов, при ко­торых будут обеспечены заданные в ТЗ параметры статических характеристик системы.

Сначала составим статические модели элементов системы. Как видно из ее функциональной схемы, система состоит из следующих элементов:

- задатчик в виде потенциометра, подключенного к источнику постоянно­
го, стабильного напряжения;

- двигатель постоянного тока независимого возбуждения;

- регулятор скорости;

- регулируемый преобразователь переменного трехфазного напряжения;

- тахогенератор.

9.3.1.1. Модель двигателя постоянного тока. Статический режим ДПТ опи­сывается следующей системой уравнений:

1) уравнение баланса напряжений для обмотки якоря

; (9.7)

2) уравнение э.д.с. вращения в обмотке якоря

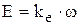; (9.8)

3) уравнение электромагнитного момента, развиваемого двигателем на валу

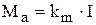; (9.9)

4) уравнение баланса моментов на валу

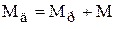; (9.10)

5) уравнение момента сил трения в системе (считаем этот момент пропор­циональным частоте вращения вала)

, (9.11)

где Н - коэффициент пропорциональности по трению.

Система уравнений (9.7-9.11) является статической моделью двигателя, и на ее основе могут быть получены все его статические характеристики. Для по­лучения какой-либо характеристики в этих уравнениях выбирают зависимую переменную и одну или несколько независимых переменных. Так, например, для механической характеристики двигателя, которая определяется выраже­нием , зависимой переменной, является 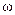, а независимыми пере­менными U и М.

Решение уравнений можно проводить различными методами, например, пу­тем последовательного исключения лишних переменных, путем представле­ния модели в матричной форме и т.д. Покажем метод решения с помощью структурной схемы, и будем пользоваться им в дальнейшем.

Модель, записанную в виде системы уравнений, заменим эквивалентной ей структурной схемой. Для построения этой схемы проведем следующие пре­образования исходных уравнений.

Уравнение (9.7) перепишем так

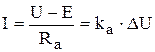, (9.12)

где .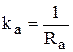

Уравнения (9.10-9.11) объединим и запишем в виде

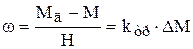, (9.13)

Уравнения (9.8) и (9.9) оставим без изменений.

Теперь каждое уравнение системы можно трактовать как уравнение звена, на входе которого действует независимая переменная, а на выходе - зависи­мая. Из таких звеньев можно построить структурную схему двигателя. Она представлена на рис. 9.2.

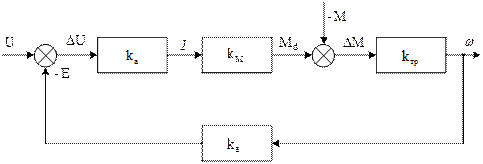
Рис. 9.2. Структурная схема ДПТ независимого возбуждения при якорном регулировании

Последовательность получения статической характеристики с помощью струк­турной схемы состоит в следующем: на структурной схеме определяют точку дей­ствия нужной независимой переменной и считают ее входом, и точку действия нужной зависимой переменной и считают ее выходом. После этого структурную схему преобразуют в эквивалентное звено относительно этих точек. Преобразо­вание схемы можно сделать либо путем последовательных упрощений, либо по правилу Мейсона. В дальнейшем будем пользоваться правилом Мейсона [2].

В качестве примера определим статическую характеристику двигателя . Так как в характеристике две независимых переменных U и М, то структурную схему преобразуем дважды: относительно точек U, 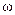и отно­сительно точек М, 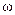. Преобразование схемы относительно первой пары точек дает передаточную функцию

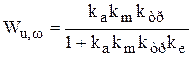. (9.14)

Аналогичное преобразование относительно точек М и 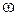дает передаточ­ную функцию

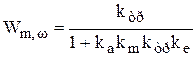. (9.15)

Так как модель двигателя линейная, то для записи его характеристики вос­пользуемся принципом суперпозиции реакций, т.е.

. (9.16)

В дальнейшем будет использоваться и такая запись этой характеристики

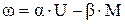. (9.17)

9.3.1.2.Модель регулятора скорости. В качестве регулятора скорости используем безынерционный усилитель с коэффициентом передачи k_с. Так как
этот усилитель передает сигнал без искажения формы, изменяя лишь его мас­штаб, то математической моделью регулятора будет уравнение

. (9.18)

9.3.1.3.Модель преобразователя напряжения. Для регулирования напря­жения на якоре двигателя используем трехфазный полностью управляемый
преобразователь с косинусным принципом регулирования фазы. В таком пре­образователе имеет место линейная зависимость между его выходным напря­жением U и сигналом управления U_y. Поэтому можно записать

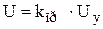. (9.19)

9.3.1.4.Модель тахогенератора. Тахогенератор является устройством из­мерения частоты вращения и изготавливается так, что с высокой точностью
его напряжение пропорционально частоте вращения, то есть

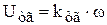. (9.20)

9.3.1.5.Модель САР. Модель системы составляется на основе ее функциональной схемы (рис. 9.1). Запись уравнений начнем с входа системы, на который
поступает сигнал задания U_з. Этот сигнал поступает на элемент сравнения, на
выходе которого вырабатывается сигнал ошибки регулирования 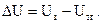Это уравнение часто называют также уравнением замыкания системы. Остальные уравнения модели САР читателю уже знакомы - они яв­ляются уравнениями элементов. В результате получаем статическую модель проектируемой автоматической системы в следующем виде:

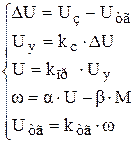(9.21)

По этим уравнениям составляется структурная схема системы (рис. 9.3).

Рис. 9.3. Структурная схема САР (статика)

На основе этой структурной схемы могут быть получены все статические характеристики системы.

Так как в расчетах системы используется ее механическая характеристика

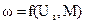, то на примере этой характеристики покажем принцип построе­ния характеристик САР.

Поскольку в данной характеристике участвуют два внешних воздействия

(U_з и М), то структурную схему (рис. 9.3) преобразуем дважды: относительно

точек U_з, 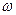и относительно точек М, 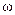и используем принцип суперпози­ции. Это дает выражение характеристики

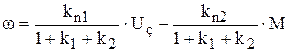, (9.22)

где k_n1 = k_ck_прk_ak_mk_тр – коэффициент передачи прямого пути от U_з к ;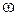

k_n2 = k_тр – коэффициент передачи прямого пути от М к ;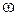

k₁ = k_ak_mk_трk_c; k₂ = k_n1k_тг.

Для полного анализа статических свойств автоматической системы чита­телю следует самостоятельно получить также другие статические характерис­тики:

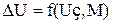- - статическая ошибка регулирования;

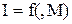- - токовая характеристика системы;

9.3.1.6.Расчет параметров настройки. Рассчитать параметры настройки -это значит найти такие значения коэффициентов передачи элементов, при ко­торых выполняются условия технического задания. При этом к параметрам настройки могут быть отнесены только те коэффициенты передачи, которые допускают независимое регулирование своей величины. В данной системе та­кими коэффициентами являются:

к_с - коэффициент передачи регулятора скорости;

к_пр - коэффициент передачи преобразователя;

к_тг - коэффициент передачи тахогенератора.

Остальные коэффициенты к параметрам настройки отнести нельзя, т.к. их значения определяются либо паспортными данными двигателя, либо парамет­рами самой системы.

Сначала определим коэффициенты передачи, которые не относятся к группе параметров настройки. Из уравнений модели двигателя и системы получим

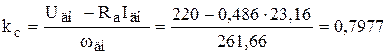В/с. (9.23)

Нм/А. (9.24)

Ом^-1. (9.25)

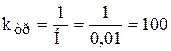Нмс^-1 (9.26)

Для определения параметров настройки воспользуемся данными техни­ческого задания и уравнением механической характеристики системы (9.22).

Так как по техническому заданию система должна обеспечивать при мак­симальной частоте вращения статизм механической характеристики не хуже S_xc во всем диапазоне нагрузок, то, пользуясь определением "статизма характери­стики системы", можно записать

, (9.27)

где 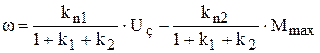- частота вращения системы при максимальном моменты на ее валу;

- частота вращения системы в режиме холостого хода;

Совместное решение этих уравнений относительно неизвестных k_с, k_пр, k_тг даст формулы для расчета параметров настройки. Эти формулы предлагаем читателю получить самостоятельно, а здесь приведем значения этих параметров

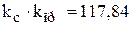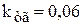; . (9.28)

Дата добавления: 2014-11-29