Динамическая модель САР

В уравнениях динамической модели присутствует координата времени, и поэтому модель представляет собой систему дифференциально-алгебраичес­ких уравнений.

Примечание. Так как решение модели будет проводиться с помощью ин­тегральных преобразований Лапласа, то для сокращения записи уравнений в изображениях функциональные зависимости от переменной "р" будем под­черкивать волнистой линией, например вместо U(p) будем писать Ũ и т.д.

9.3.2.1. Модель ДПТ. Так как при якорном регулировании двигателя пара­метры цепи возбуждения остаются постоянными, то динамика процессов дви­гателя будет определяться следующей системой уравнений:

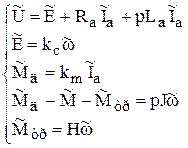(9.29)

Эта модель линейная, и к ней можно применить преобразование Лапласа. Изоб­ражения уравнений при нулевых начальных условиях имеют следующий вид:

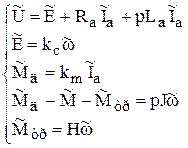(9.30)

Для записи модели в виде структурной схемы сделаем следующие преоб­разования:

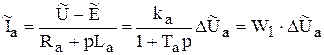, (9.31)

где k_a – коэффициент передачи динамического звена;

Т_а = L_a/R_a – электромагнитная постоянная времени звена; 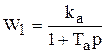- передаточная функция звена;

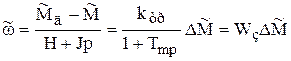, (9.32)

где k_тр – коэффициент передачи звена;

Т_m = J/H – механическая постоянная времени звена; 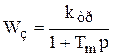- передаточная функция звена.

Второе и третье уравнения в формуле (9.30) не нуждаются в преобразовани­ях, т.к. они уже определяют звенья с передаточными функциями

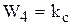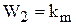, . (9.33)

Структурная схема двигателя приведена на рис. 9.4.

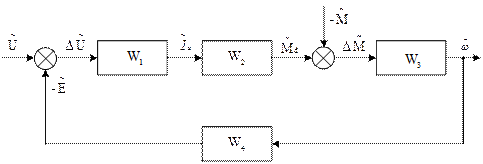
Рис. 9.4. Структурная схема ДПТ (динамика)

9.3.2.2. Модель П-регулятора скорости. Этот элемент осуществляет фор­мирование закона регулирования скорости и, поскольку по техническому заданию система "статическая", использован пропорциональный регулятор, для
которого справедливо

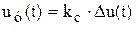, (9.34)

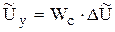, (9.35)

где W_c = k_c – передаточная функция регулятора.

9.3.2.3. Модель преобразователя напряжения. Считаем преобразователь
безынерционным усилителем, и тогда можно записать

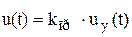, (9.36)

, (9.37)

где W_пр = k_пр – передаточная функция преобразователя.

9.3.2.4. Модель тахогенератора. Если пренебречь электромагнитной инер­ционностью тахогенератора, то можно записать

, (9.38)

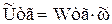, (9.39)

где W_тг = k_тг – передаточная функция тахогенератора.

9.3.2.5. Модель САР. Модель составляется на основе функциональной схемы
(рис. 9.1) и представляет собой следующую систему операторных уравнений:

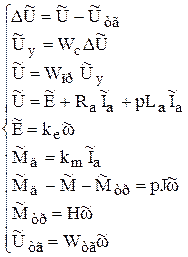(9.40)

Структурная схема САР, построенная по этой системе уравнений, представ­лена на рис. 9.5.

Для упрощения достаточно громоздких преобразований, которые обычно сопровождают расчеты САР, введем для всех передаточных функций новое однотипное обозначение в виде дроби, перенося на числитель и знаменатель индекс передаточной функции, например

.

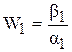Сведем передаточные функции системы в табл.9.1.

Таблица 9.1

Передаточные функции системы

Wi	W1	W2	W3	W4	Wc	Wпр	Wтг
βi	ka	ka	kтр	ke	kc	kпр	kтг
αi	1+Tap		1+Тmp

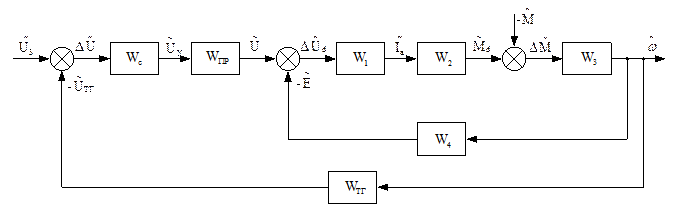
Рис. 9.5. Структурная схема CAP (динамика)

Дата добавления: 2014-11-29