Анализ динамики САР

9.3.3.1. Динамические характеристики САР. Динамической характерис­тикой САР является функциональная зависимость между переменными моде­ли. Последовательность получения характеристик на основе структурной схе­мы показана в параграфе 9.3.1.1. Здесь следует напомнить читателю, что струк­турные схемы дают только операторное выражение характеристик, а для полу­чения характеристик в реальных переменных потребуется выполнить обрат­ное преобразование Лапласа.

Динамика частоты вращения вала системы 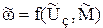. В качестве не­зависимых переменных здесь выступают возмущающие воздействия: Ũ₃ - на­пряжение задания и 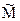- момент нагрузки на валу системы. Линейность моде­ли позволяет получить искомую характеристику как сумму характеристик от отдельных возмущений, т.е.

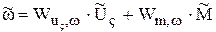, (9.41)

где и 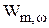- передаточные функции системы относительно точек , и , .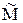

Относительно точек , структурная схема имеет один прямой путь W_cW_прW₁W₂W₃ и два контура с обратными отрицательными связями W_cW_прW_lW₂W₃W_тг и W₁W₂W₃W₄. Это позволяет записать передаточную функцию по правилу Мейсона следующим образом:

.

или после исключения по знаку *

.

Подставим в последнюю формулу значения передаточных функций по табл. 9.1 и после упрощений получим

. (9.42)

В записи этой формулы принято следующее: произведения одноименных ко­эффициентов сокращенно записываются так 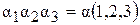. После подстановки данных из табл. 9.1 получим

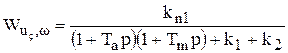. (9.43)

Аналогичные преобразования структурной схемы относительно точек , дают

,

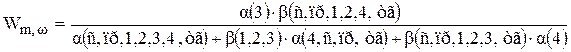или

. (9.44)

Здесь принято: , .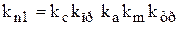

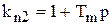Таким образом, операторное выражение механической характеристики си­стемы будет следующим:

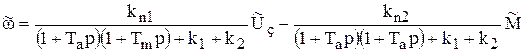. (9.45)

Для анализа динамических свойств системы необходимо получить само­стоятельно другие характеристики:

; .

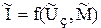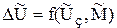9.3.3.2. Характеристическое уравнение САР. Читатель заметил, что в пере­даточных функциях и 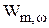, которые участвуют в описании механи­ческой характеристики системы, одинаковый знаменатель. И это совпадение не случайное - из теории автоматического управления известно, что любая другая передаточная функция системы будет иметь такой же знаменатель. Выражение знаменателя называется характеристическим уравнением системы, и оно описывает свободное движение системы.

Характеристическим уравнением системы является полином второй сте­пени

; (9.46)

где ; ; .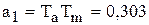

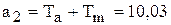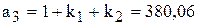9.3.3.3. Проверка системы на устойчивость. Характеристическое уравне­ние системы используется для проверки ее на устойчивость. Но поскольку
данная система имеет характеристическое уравнение второго порядка, то, по известным положениям теории устойчивости, для нее необходимым и дос­таточным условием устойчивости является положительность всех коэффици­ентов ее характеристического уравнения. По результатам расчета этих коэф­фициентов делаем вывод, что данная система устойчива.

Построение годографа Михайлова. Годограф Михайлова относится к од­ному из методов определения устойчивости системы, и его уравнение получа­ется из характеристического уравнения системы заменой оператора " " на " "

(9.47)

или

, .

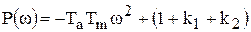Годограф строится на комплексной плоскости 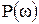, при изменении . Годограф устойчивой системы должен охватывать начало коорди­нат и проходить против часовой стрелки столько квадрантов, каков порядок характеристического уравнения. Годограф системы начинается в первом квад­ранте и в четвертом уходит в бесконечность.

9.3.3.4. Построение переходных характеристик САР. Переходная харак­теристика определяет переходный процесс в автоматической системе, когда на нее действует ступенчатое возмущение. Для построения переходной харак­теристики надо от ее изображения перейти к оригиналу. Это делается с помо­щью обратного преобразования Лапласа.

В качестве примера проведем построение переходной характеристики

, которая определяет динамику изменения частоты враще­ния вала системы при действии на нее двух возмущений: напряжения зада­ния U_з(t) и момента сопротивления на валу M(t). Изображение этой характе­ристики дано в уравнении (9.45), но для использования этой формулы требуется задать законы изменения возмущений. Так как по условию построения пере­ходной характеристики эти возмущения должны иметь ступенчатую форму, то запишем

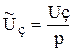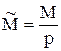, , (9.48)

где U_з и М - значения реальных физических сигналов, действующих в авто­матической системе. Тогда окончательный вид изображения характеристики будет таким

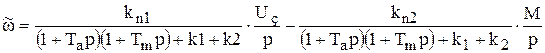(9.49)

Запишем эту формулу следующим образом:

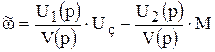, (9.50)

где 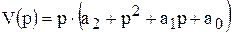- полином третьей степени, имеет три корня. Эти корни определяются из уравнения V(p) = 0 и имеют следующие значения:

(9.51)

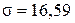где и 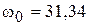- определяют соответственно затухание и частоту

свободных колебаний переходного процесса системы.

Так как V(p) = 0 не имеет кратных корней, то оригинал для (9.49) определя­ем по формуле разложения вида

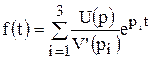, (9.52)

где V’(p) = 3a₂p²+2a₁p+a₀ – производная от V(p).

По формуле разложения получим искомую переходную характеристику, кото­рую запишем в таком виде

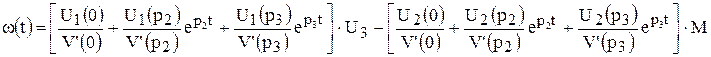Но поскольку корни р₂, р₃ комплексные, то и переходная характеристика будет записана в комплексной форме. Преобразование комплексной формы в веществен­ную покажем на примере первого слагаемого в формуле (9.53), которое имеет вид

.

Далее запишем и , где 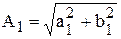, , 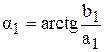и по формуле Эйлера найдем

.

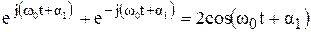В результате комплексное выражение запишется в вещественной форме

. (9.53)

После проведения указанных преобразований переходная характеристика системы будет описываться следующим уравнением:

. (9.54)

ЗАКЛЮЧЕНИЕ

В методических указаниях показаны основные принципы начального эта­па разработки автоматической системы. Это первичная компоновка схемы, оп­ределение параметров настройки и расчеты статических и динамических ха­рактеристик. На этом этапе разработки схема содержит только функциональ­но необходимые элементы. Расчет параметров качества регулирования, режим­ных параметров и т.д. наверняка покажет, что этот первичный вариант требует доработок.

Опыт разработок автоматических систем показывает, что в системах, со­стоящих только из функционально необходимых элементов, обычно не удает­ся получить требуемые показатели качества. Это объясняется тем, что требо­вания, предъявляемые к характеристикам системы, обычно носят противоре­чивый характер. Например, повышение точности системы в установившемся режиме требует повышения коэффициента усиления системы, но это всегда уменьшает запас устойчивости системы и ухудшает переходный процесс. При этом чаще всего система становится неустойчивой раньше, чем удастся полу­чить требуемый коэффициент усиления.

Поэтому на следующем этапе разработки решается вопрос, правильно ли скомпонована схема, и какими методами ее улучшать. Но эти вопросы уже выходят за рамки курса и в данной работе не обсуждаются.

Дата добавления: 2014-11-29