Учебное пособие. Запитання та завдання

Ю. М. ЖУЧЕНКО

Учебное пособие

Ю. М. ЖУЧЕНКО

Запитання та завдання

1. Назвати функції фільтрів НВЧ, навести їх класифікацію. Пояснити типові характеристики та параметри фільтрів.

2. Пояснити, у чому еквівалентні схеми смугових фільтрів НВЧ із l/4-зв’язками та LC- ФНЧ.

3. У чому полягає принцип розрахунку фільтрів із чвертьхвильовими та безпосередніми зв’язками?

4. Навести приклади конструкцій фільтрів із чвертьхвильовими та безпосередніми зв’язками. Які особливості цих фільтрів?

5. У чому полягають особливості властивостей і конструкцій фільтрів на діелектричних і феритових резонаторах

6. Назвати вимоги до параметрів частотно-розділових пристроїв. Навести приклади їх конструктивного виконання.

7. Пояснити принцип дії фільтрів, показаних на рис. 1.86.

8. Побудуйте графік амплітудно-частотної характеристики, визначте смугу пропускання і добротність фільтру, у якого на частоті 10 ГГц КСХ рівний одиниці, при збільшенні частоти з дискретністю 10 МГц КСХ відповідно був рівний 1,5; 2,6; 17,8; 65.

9. Визначите довжину камери хвилевідного смугового фільтру, утвореного двома індуктивними діафрагмами товщиною 1 мм, з розміром вікна 38 мм, установленим в хвилеводі з розмірами 90´45 мм. Резонансна частота фільтру рівна 2380 МГц.

10. Хвилевідний смуговий фільтр складається з двох однакових індуктивних діафрагм, встановлених в хвилеводі з розмірами 72´34 мм. Резонансна частота фільтру рівна 3 ГГц, смуга пропускання складає 19 МГц. Розрахуйте добротність фільтру, довжину камери, провідність діафрагм і розмір їх вікон.

11. Визначите довжину камери хвилевідного смугового фільтру, утвореного двома ємкісними діафрагмами з нормованою провідністю рівною 1,2 при частоті 10 ГГц. Діафрагми встановлені в хвилеводі з розмірами 23´10 мм.

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
В БИОЛОГИИ И ХИМИИ

Гомель 2010

Министерство образования Республики Беларусь

Учреждение образования

«Гомельский государственный университет

имени Франциска Скорины»

МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
В БИОЛОГИИ И ХИМИИ

для студентов вузов, обучающихся по специальности
1-31 01 01 «Биология»

Гомель 2010

УДК 57; 004.9+54; 004.9 (075.8)

ББК 28c51+24c51я73

Ж 834

Рецензенты:

А.С. Кобайло доцент, к.т.н., доцент кафедры ИСиТ Белорусского государственного технологического университета;

Н.Г. Еремова доцент, к.б.н., доцент кафедры общей экологии и методики преподавания биологии Белорусского государственного университета.

Рекомендовано к изданию научно – методическим советом учреждения образования «Гомельский государственный университет имени Франциска Скорины»

Жученко, Ю. М.

Ж 834 Математическая статистика в биологии и химии: учебное пособие для студентов вузов по специальности
1-31 01 01 «Биология» / Ю. М. Жученко; М-во образования РБ, Гомельский гос. ун-т им. Ф. Скорины. – Гомель: ГГУ
им. Ф. Скорины, 2010.– 197 с.

ISBN

Целью учебного пособия является оказание помощи студентам в усвоении основ курса математической статистики в биологии и химии, обработки результатов экспериментов с применением возможностей персональных компьютеров.

Учебное пособие адресовано студентам специальности
1-31 01 01 “Биология”.

УДК 57; 004.9+54; 004.9 (075.8)

ББК 28c51+24c51я73

ISBN Ó Жученко Ю. М., 2010

Ó УО «Гомельский

государственный

университет им Ф. Скорины», 2010

Основные условные обозначения в математической статистике

X_i, Y_j, Z_k – случайные переменные (дискретные или непрерывные);

р – вероятность ожидаемого дискретного события;

q – вероятность противоположного дискретного события;

m – частота появления ожидаемого события;

n – число испытаний;

p_i – вероятность i–го дискретного события;

f(x) – плотность вероятности непрерывной случайной переменной;

E(X) – математическое ожидание случайной переменной;

D²(X) – дисперсия;

D(X) – стандартное (среднеквадратическое отклонение);

μ – среднее арифметическое выборки;

σ² – дисперсия выборки;

σ – стандартное (среднеквадратическое отклонение) выборки;

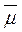– среднее арифметическое генеральной совокупности;

– дисперсия генеральной совокупности;

– стандартное (среднеквадратическое) отклонение генеральной совокупности;

G – средняя геометрическая;

H – средняя гармоническая;

S – средняя квадратическая;

М₀ – мода;

М_е – медиана;

ν – число степеней свободы;

V – коэффициент вариации;

– нормированное отклонение;

– средняя суммарной группы;

– стандартное отклонение (сигма) суммарной группы;

А – скошенность (асимметрия) кривой распределения;

Е – крутизна (эксцесс) кривой распределения;

±Δ – доверительные границы;

t – критерий надежности;

F – критерий Фишера;

β₁, β₂, β₃ – три основных порога вероятности безошибочных прогнозов;

χ² – критерий согласия Пирсона;

λ – критерий согласия Колмогорова – Смирнова;

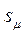– ошибка репрезентативности выборочного показателя;

– ошибка коэффициента вариации;

– ошибка разности средних;

– ошибка показателя асимметрии;

– ошибка показателя асимметрии;

– ошибка показателя эксцесса;

r – парный коэффициент корреляции;

– ошибка коэффициента корреляции;

R_y/x – коэффициент регрессии;

– ошибка коэффициента регрессии;

r_xy-z, r_xz-y, r_zy-x – частные коэффициенты корреляции;

R_x-yz, R_y-xz, R_z-yx – множественные коэффициенты корреляции;

η_yx – корреляционное отношение;

– ошибка репрезентативности корреляционного отношения;

С_i – сумма квадратов факториальных, случайной и общей центральных отклонений (С_V, С_А, С_B, С_АB, C_Z, С_Y);

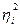– сила влияния.

Содержание

Основные условные обозначения в математической статистике 3

Введение 8

ТЕМА 1 Основы теории вероятностей. 9

1.1 Предмет и метод математической статистики. 9

1.2 Понятие случайного события. 12

1.3 Вероятность случайного события. 15

1.4 Основные теоремы теории вероятностей. 17

ТЕМА 2 Случайные переменные. 21

2.1 Понятие случайной переменной. 21

2.2 Математическое ожидание и дисперсия. 24

2.3 Моменты 28

ТЕМА 3 Дискретные распределения. 30

3.1 Биномиальное распределение и измерение вероятностей. 30

3.2 Распределение редких событий (Пуассона) 34

ТЕМА 4 Основные модели теоретических распределений. 37

4.1 Прямоугольное (равномерное) распределение. 37

4.2 Нормальное распределение. 38

4.3 Логарифмически нормальное распределение. 43

ТЕМА 5 Распределения параметров выборки. 46

5.1 t – распределение Стьюдента. 46

5.2 F-распределение Фишера–Снедекора. 49

5.3 χ²–распределение. 50

ТЕМА 6 Основы математической статистики. 53

6.1 Средние величины.. 53

6.2 Средняя арифметическая. 57

6.3 Средняя геометрическая. 65

6.4 Средняя гармоническая. 68

ТЕМА 7 Разнообразие значений признака. 71

7.1 Стандартное (среднеквадратическое) отклонение. 71

7.2 Проверка выпадов (артефактов) 78

7.3 Средняя и сигма суммарной группы.. 79

7.4 Скошенность (асимметрия) и крутизна (эксцесс) кривой распределения 80

ТЕМА 8 Графическое представление распределений. 82

8.1 Вариационный ряд. 82

8.2 Гистограмма и вариационная кривая. 84

8.3 Кумулята 85

8.4 Достоверность различия распределений. 86

ТЕМА 9 Нормальное распределение. 93

9.1 Генеральная совокупность и выборка. 93

9.2 Репрезентативность. 96

9.3 Ошибки репрезентативности и другие ошибки исследований. 97

9.4 Доверительные границы.. 100

ТЕМА 10 Оценка генеральных параметров. 103

10.1 Общий порядок оценки. 103

10.2 Критерий достоверности разности. 113

10.3 Репрезентативность при изучении качественных признаков. 116

10.4 Достоверность разности долей. 119

ТЕМА 11 Парная корреляция. 122

11.1 Коэффициент корреляции. 122

11.2 Ошибка коэффициента корреляции. 127

11.3 Уравнение прямолинейной регрессии. 132

11.4 Ошибки элементов уравнения прямолинейной регрессии. 135

ТЕМА 12 Частная и множественная линейные корреляции и регрессии 138

12.1 Частный коэффициент корреляции. 138

12.2 Множественный коэффициент корреляции. 141

12.3 Линейное уравнение множественной регрессии. 142

ТЕМА 13 Криволинейная корреляция и регрессия. 144

13.1 Корреляционное отношение. 144

13.2 Свойства корреляционного отношения. 149

13.3 Ошибка репрезентативности корреляционного отношения. 150

13.4 Критерий линейности корреляции. 152

ТЕМА 14 Однофакторный дисперсионный анализ. 154

14.1 Сущность и метод дисперсионного анализа. 154

14.2 Однофакторный дисперсионный комплекс. 159

ТЕМА 15 Многофакторный дисперсионный анализ. 162

15.1 Многофакторный дисперсионный комплекс. 162

15.2 Преобразования. 164

15.3 Универсальное использование дисперсий. 165

ТЕМА 16 Классификация. 177

16.1 Дискриминантный анализ. 177

16.2 Кластерный анализ. 181

Литература 188

Приложение. Основные формулы и определения. 189

Введение

Предлагаемая работа – учебное пособие по математической статистике в биологии и химии предназначено, прежде всего, для биологов. Этим определяется как принятая в ней тематическая структура, содержание приводимых примеров, так и самый метод изложения материала. Считаясь с тем, что рядовой читатель этой книги не будет иметь математического образования, а только тот запас сведений из этой области, который дается в настоящее время в вузах с биологическим уклоном, во многих случаях сложные математические процедуры опускаются.

В ходе изложения внимание акцентируется главным образом на практическое приложение описываемых методов; упор делается также на то, чтобы выработать у читателя определенную минимальную сноровку в «арифметике» вычисления вероятностей. Если первое необходимо для осознания большой практической ценности математической статистики, то второе может весьма пригодиться при чтении научной литературы по статистике. Довольно значительное число примеров призвано облегчить понимание текста и показать некоторые основные виды проблем, решаемых с помощью математической статистики.

Главная трудность в изложении состоит в том, что в большинстве случаев выборки, с которыми имеют дело в биологических исследованиях, не складываются из независимых наблюдений, что значительно усложняет методы статистической оценки. Существует много важных биолого-экологических проблем, которые можно решить с помощью статистико-математических методов, но методы эти весьма специфичны и, как правило, сложны.

Дано достаточно традиционное изложение. При этом исключены темы, касающиеся статистики эксперимента, и в то же время сделана попытка выделить общие принципы статистической оценки.

Усвоение материала должно помочь читателю в дальнейшем самостоятельном изучении статистических методов, а также тех разделов теории операционных исследований, где рассматриваются вероятностные и статистические модели.

ТЕМА 1 Основы теории вероятностей

1.1 Предмет и метод математической статистики

1.2 Понятие случайного события

1.3 Основные теоремы теории вероятностей

Дата добавления: 2014-11-29