Моменты

Большое значение в математической статистике имеют так называемые моменты распределения случайной переменной. В математическом ожидании большие значения случайной величины учитываются недостаточно. Дополнительной числовой характеристикой случайной величины, которая детальнее характеризует ее, являются моменты различных порядков. Не вдаваясь в подробное изложение теории моментов, приведем определение двух основных типов моментов.

Начальным моментом k -го порядка случайной переменной X называется математическое ожидание k -ой степени ее: μ_k = Е(Х^k). Центральным моментом k -го порядка случайной переменной X называется математическое ожидание k -ой степени отклонения X от ее математического ожидания: 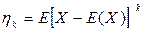. Если X – непрерывная случайная переменная, плотность вероятности которой есть f(х), то моменты μ_k и η_k вычисляют по формулам:

(2.13)

В этих формулах (с, d), как и ранее, обозначает интервал, в границах которого случайная переменная X меняет свое значение. Принимается, что моменты μ_k и η_k случайной переменной существуют тогда и только тогда, когда интегралы в формулах (2.13) являются абсолютно сходящимися. Если X – дискретная переменная, то для вычисления μ_k и η_k необходимо заменить интегралы соответствующими рядами, причем моменты существуют тогда и только тогда, когда эти ряды абсолютно сходятся.

Следует отметить, что математическое ожидание и дисперсия суть частные случаи моментов. Математическое ожидание Е(Х) есть первый начальный момент μ₁, а дисперсия D²(X) есть второй центральный момент η₂. В статистическом анализе большое значение имеют также центральные моменты третьего и четвертого порядков. Третьи центральные моменты служат для оценки степени скошенности распределения (асимметрия). О центральных моментах четвертого порядка говорят, что они измеряют степень сглаженности (эксцесс) кривой плотности вероятности.

Вопросы для самоконтроля

1 Каким образом можно представить распределение дискретной случайной переменной?

2 Дайте определение случайной переменной.

3 Дайте определение дискретной и непрерывной случайной переменной.

4 При каких условиях случайная переменная называется непрерывной?

5 Дайте определение математического ожидания и дисперсии.

6 Чему равно значение математического ожидания при одинаковой вероятности величин случайной переменной?

7 Могут ли две случайные величины обладать одинаковым математическим ожиданием и различной дисперсией? Приведите практические примеры.

8 Какова размерность среднего квадратического отклонения?

9 Моментам какого порядка соответствуют математическое ожидание и дисперсия? Приведите формулы.

10 Моментам какого порядка соответствуют степени скошенности распределения и степени сглаженности кривой плотности вероятности.

ТЕМА 3 Дискретные распределения

3.1 Биномиальное распределение и измерение вероятностей

3.2 Распределение редких событий (Пуассона)

Дата добавления: 2014-11-29