
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Прямоугольное (равномерное) распределение
|
|
|
|
Распределение редких событий (Пуассона)
Когда вероятности альтернатив неравны, т. е. р ≠ q, биномиальное распределение асимметрично. При очень малой вероятности ожидаемого события, исчисляемой сотыми или тысячными долями единицы, по сравнению с вероятностью q противоположного события распределение вероятности или частоты таких событий описывается формулой Пуассона.
Модель такого распределения получают на основе независимых испытаний при постоянной вероятности р наступления некоторого случайного события X.
Как известно, вероятность того, что в n испытаниях случайное событие наступит равно m раз, определяется формулой, выражающей функцию распределения вероятностей для биномиального распределения.
Примем теперь дополнительные условия, а именно, что вероятность р наступления случайного события в единичном испытании весьма мала, но число испытаний n весьма велико, n 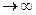 , а произведение nр (обозначим его λ) – число постоянное и не очень большое.
, а произведение nр (обозначим его λ) – число постоянное и не очень большое.
При таких дополнительных условиях на основе формулы биноминального распределения получим следующее выражение для распределения вероятностей случайной переменной X:
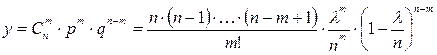 (3.3)
(3.3)
где: λ = np; р = λ/n.
Так как числитель первой дроби имеет m сомножителей, а в знаменателе стоит nm, каждый из сомножителей можно разделить на n. Получим:
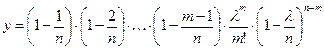 (3.4)
(3.4)
При n 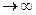 предел любой дроби (1 – λ/n) = 1,
предел любой дроби (1 – λ/n) = 1,
а предел (1 – λ/n)n-m =e-λ
При этих условиях:
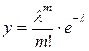 (3.5)
(3.5)
Выражение (3.5) называется функцией распределения вероятностей в распределении Пуассона.
В этом выражении m – частота ожидаемого события в n испытаниях, е = 2,7183; параметр λ = nр равен математическому ожиданию или наиболее вероятной частоте события, 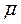 , а также дисперсии
, а также дисперсии 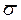 .
.
Для практических расчетов, когда находят теоретические ординаты распределения n, т. е. численности распределения случайного события X, выражение (3.5) умножают на N – общее число наблюдений, вместо 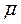 принимают экспериментальное среднее число наблюдаемых случаев. Формула для n будет:
принимают экспериментальное среднее число наблюдаемых случаев. Формула для n будет:
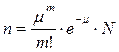 (3.6)
(3.6)
Распределение Пуассона с возрастанием средней X приближается к биномиальному. Распределение Пуассона описывает многие явления в технике и биологии. В технике оно находит широкое применение при контроле качества продукции, для аппроксимации распределения дефектных изделий. В биологии оно применяется как модель распределения числа семян сорняков – примесей в пробных навесках при анализе семян, поврежденных вредителем. Оно описывает также распределение численности возобновления, когда размер элементарных учетных площадок очень мал или условия заселения, площади неблагоприятны, так что вероятность благоприятного исхода р мала.
Вопросы для самоконтроля
1 Что такое биномиальная кривая распределения? Какая общая формула является основой для биномиального распределения?
2 Для анализа какого вида случайных переменных используются биномиальное распределение и распределение Пуассона?
3 Что такое n в биноме (р + q)n?
4 Какими параметрами характеризуется биномиальное распределение?
5 Является ли биномиальное распределение дискретным или непрерывным?
6 Чем отличается распределение Пуассона от биномиального?
7 Какие параметры биномиального распределения можно получить с помощью треугольника Паскаля и формулы Я. Бернулли?
8 При каких условиях предпочтительнее применять распределение Пуассона?
9 При каких условиях распределение Пуассона приближается к биномиальному?
10 Какими параметрами характеризуется распределение Пуассона?
11 Что означают максимальное значение и крайние левые и правые значения на графике кривой биномиального распределения?
ТЕМА 4 Основные модели теоретических распределений
4.1 Прямоугольное (равномерное) распределение
4.2 Нормальное распределение
4.3 Логарифмически нормальное распределение
Прямоугольное (равномерное) распределение — простейший тип непрерывных распределений. Если случайная переменная X может принимать любое действительное значение в интервале (а, b), где а и b – действительные числа, и если каждому значению случайной переменной соответствует одинаковая плотность вероятности, то переменная X имеет прямоугольное распределение. Иногда пользуются термином «равномерное распределение».
Из приведенного определения следует, что плотность распределения вероятностей этой случайной переменной должна быть постоянной, т. е. что в интервале (a, b) f(x) = с. Отсюда, а также из условия, что интеграл от функции f(x), взятый в интервале (а, b), должен равняться единице, нетрудно найти функцию плотности вероятности f(x). Имеем:
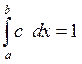 (4.1)
(4.1)
откуда cb – са = 1 и, следовательно, получим 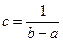 . Таким образом, функция плотности вероятности для прямоугольного распределения:
. Таким образом, функция плотности вероятности для прямоугольного распределения:
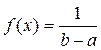 для a ≤ x ≥ b. (4.2)
для a ≤ x ≥ b. (4.2)
Для х > b и х < а плотность равняется нулю. Нетрудно вычислить математическое ожидание и дисперсию рассматриваемой случайной переменной. Имеем:
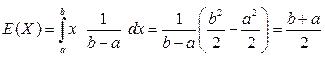 (4.3)
(4.3)
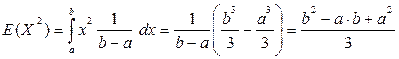 (4.4)
(4.4)
Отсюда находим, что дисперсия D2(X) равняется:
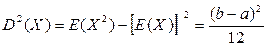 (4.5)
(4.5)
Прямоугольное распределение находит широкое применение в математической статистике. Оно имеет основополагающее значение для так называемых непараметрических методов – одного из новейших разделов статистики, находящего все более широкое применение. Понятием прямоугольного распределения иногда пользуются и в теории статистических оценок – в том разделе статистики, где изучаются методы построения выводов о значениях параметров в генеральной совокупности на основании случайной выборки. В некоторых теориях статистического вывода за исходный пункт принимается правило: что, если нам ничего неизвестно о значении оцениваемого параметра, то следует принять, что каждое его значение равновозможно. Это ведет к истолкованию оцениваемого параметра как случайной переменной, характеризующейся прямоугольным распределением.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 1382; Нарушение авторских прав?; Мы поможем в написании вашей работы!