Средняя гармоническая

Средняя гармоническая рассчитывается по формуле

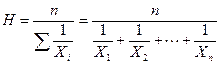. (6.14)

Для пяти вариантов: 1, 4, 5, 5 средняя гармоническая:

.

Применяется средняя гармоническая при усреднении меняющихся скоростей.

Пример

Почтовые голуби одной станции к месту кормежки летят со скоростью 50 км/час, а в обратном направлении – со скоростью 40 км/час. Если ничего больше неизвестно и требуется выяснить среднюю скорость полета для обоих направлений (расстояния, очевидно, равны), то сделать это можно, рассчитав простую среднюю гармоническую для двух значений 50 и 40:

.

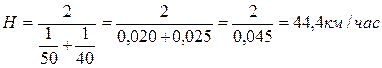Пример

Рысак на тренировках пробегал одну за другой три дистанции, различные по состоянию дороги. Скорость на первой дистанции составляла 13 км/час, на второй – 25 км/час и на третьей – 10 км/час. Длина дистанций не сообщается: известно, что первая дистанция была в 2 раза, а вторая в 4 раза длиннее третьей. По этим данным можно определить показанную рысаком среднюю скорость по всем трем дистанциям, рассчитав не простую, а взвешенную среднюю гармоническую из значений 13, 20, 10 соответственно с весами 2, 4, 1 по формуле:

. (6.15)

Взвешивание скоростей производится обычно по расстояниям. Поскольку в данном примере расстояния неизвестны, то весами могут служить отношения первой и второй дистанции к третьей. Такая замена математических весов не повлияет на точность результата, так как для правильного расчета взвешенной средней гармонической имеют значение не абсолютные величины расстояний, а их отношения

.

Вопросы для самоконтроля

1 Каковы основные свойства средних величин?

2 Какие средние величины используются в биологии?

3 По какой схеме между минимальным и максимальным значениями признака расположены средние значения?

4 По какому признаку (суммарному результату) следует выбирать для расчетов ту или иную среднюю?

5 Каковы математические свойства средней арифметической?

6 Какими двумя способами можно рассчитывать среднюю из относительных величин?

7 Что означает ранжирование признаков объекта?

8 В каких случаях применяется взвешенная средняя?

9 В каких случаях целесообразно пользоваться средней геометрической? Формула средней геометрической и ее преобразование с помощью логарифмов.

10 Приведите пример в биологии для применения средней квадратической.

11 Необходимо ли знать фактические длины для вычисления средней скорости на нескольких разных дистанциях или достаточно знать их соотношение?

12 Что характеризует мода распределения?

13 Может ли квантиль совпадать с медианой?

14 Дать определения квантиля, квартиля, дециля и перцентиля.

15 Могут ли совпасть значения средней арифметической, медианой и модой?

ТЕМА 7 Разнообразие значений признака

7.1 Стандартное (среднеквадратическое) отклонение

7.2 Проверка выпадов (артефактов)

7.3 Средняя и сигма суммарной группы

7.4 Скошенность (асимметрия) и крутизна (эксцесс) кривой распределения

Всякая группа состоит из особей или объектов, отличающихся друг от друга по каждому из признаков. Различия эти иногда очень велики, иногда они почти незаметны, но они всегда имеются в группе, так как невозможно найти даже двух абсолютно одинаковых особей. Это второе основное свойство всякой группы – состоять из неодинаковых объектов по любому признаку – точнее всего определяется термином разнообразие признака в группе.

Часто этому групповому свойству даются другие названия: изменчивость, рассеяние, колеблемость, вариабильность, разброс.

Дата добавления: 2014-11-29