Хвильові матриці простих чотириполюсників та восьмиполюсників

Зв’язок елементів матриць передачі та розсіювання

Елементи матриці [ T ] можна виразити черезелементи матриці [ S ]:

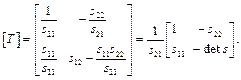(1.17)

Для оборотного чотириполюсника s₁₂ = s₂₁ і визначник матриці [ T ] дорівнює одиниці:

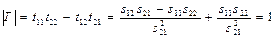. (1.18)

З урахуванням виразу (1.18) коефіцієнт 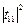можна записати у вигляді

використавши властивість унітарності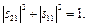

Аналогічно елементи матриці [ S ] можна виразити черезелементи матриці [ T ]:

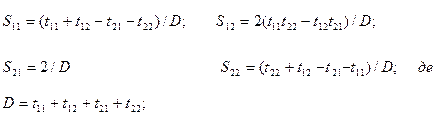(1.19)

. Наведемо приклад використання матриці [ S ].

Розглянемо ділянку ЛП електричною довжиною , у якої поширюється Т - хвиля. Ділянка нескінченного регулярного хвилеводу (рис.1.10. а) не відбиває хвилю, тому s ₁₁ = s ₂₂ = 0. Переміщення хвилі від одного входу до іншого супроводжується зміною її фази на q₀, тому .

Матриця розсіювання такого відрізка має вигляд

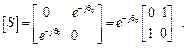(1.20)

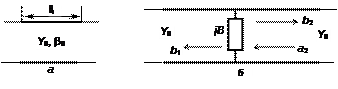Зі співвідношення (1.17) знайдемо елементи матриці [ T ] ділянки лінії: t ₁₁ = t ₁₂ =

0, t ₂₁ = 0, t ₂₂ = , тобто . (1.21)

Тепер розглянемо реактивну провідність jВ, включену в ЛП паралельно(рис. 1.10. б). Коефіцієнти відбиття s ₁₁ і s ₂₂ від реактивної провідності визначимо за формулою, отриманою в теорії довгих ліній, що пов’язує коефіцієнти відбиття s ₁₁ = s ₂₂ від навантаження Y _н = jB + Y ₀ із хвильовою провідністю лінії Y ₀:

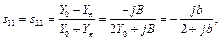
де b = B / Y ₀ – нормована реактивна провідність.

Знайдемо коефіцієнт передачі s ₂₁ = s ₁₂ за означенням як відношення амплітуд хвилі а ₂, що падає, та b ₁ – тієї, що пройшла:

.

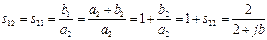Тут використано безперервність дотичних складових поля з обох боків тонкої неоднорідності - рівність амплітуди хвилі, що пройшла, сумі амплітуд хвилі, що падає, та відбитої (b ₁= а ₂+ b ₂). Як і в попередньому випадку, елементи матриці [ T ] визначимо зі співвідношення (1.17):

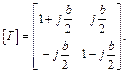(1.22)

З огляду на рівність (1.17) унесене ослаблення можна подати у вигляді

.

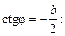Матрицю (1.22) іноді записують у параметричній формі, вводячи

такий параметр j, що

(1.22.а)

Нехай вихід чотириполюсника, матриця [ S ] якого відома, навантажений на довільне

навантаження, яке має комплексний коефіцієнт відбиття Г (рис. 1.10.в).

Знайдемо коефіцієнт відбиття від входу чотириполюсника s ₁₁із урахуванням впливу цього навантаження. Для чотириполюсника правдиві рівняння

У випадку неузгодженого навантаження а ₂ = b ₂Г ¹ 0, і з першого рівняння випливає, що

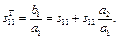(1.23)

Із другого рівняння з урахуванням того, що b ₂ = a ₂/Г, маємо

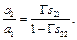. (1.24)

Підставимо праву частину співвідношення (1.24) у вираз (1.23) і одержимо

. (1.25)

Матриці стику двох хвилеводів, яки мають однаковий розмір широкої стінки а, але

різні вузькі стінки, наприклад b ₂ > b ₁ (рис.1.11), і в разі поширення в обох хвилеводах тільки основної хвилі, можна виразити у наступному виду

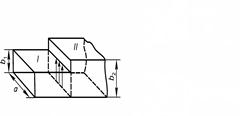
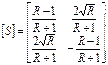; , (1.26)

де 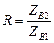- відношення хвильових опірив.

Матриця направленого восьмиполюсника (рис. 1.12) має вид:

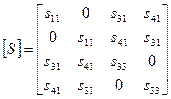
, (1.27)

яка правдива для направлених відгалужувачів, що ділять вхідну потужність між йох вихідними плечима в заданому співвідношенні.

Трьох децибельним направленим відгалужувачем або мостом називають чотирьохплечивий вузол, якій поділяєть потужність хвилі, що надходить до кожного з входів моста, нарівно між протилежними плечима. Вони поділяються на сінфазно-протифазні та квадратурні і йох матриці відрізняються. Наприклад, аналізуючи матрицю розсіювання подвійного хвилевідного трійника (рис. 1.13), можна виявити важливі його властивості, які важко пояснити міркуваннями якісного характеру.

Сформулюємо ці властивості у вигляді теореми:

якщо подвійний трійник узгоджений з боку Е - та H- пліч (s ₃₃ = s ₄₄ = 0), то:

· він узгоджений і з боку бічних пліч (s ₁₁ = s ₂₂ = 0);

· зв’язку між бічними плечима немає (s ₁₂ = s ₂₁ = 0);

· потужність, що підводиться до одного з бічних пліч, поділяється

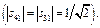нарівно між Е - та H- плечима

Для доведення перетворимо матрицю розсіювання подвійного трійника з урахуванням умов цієї теореми, взаємності пристрою – симетрії матриці [ S ] щодо головної діагоналі, а

також властивостей трійника, установлених у результаті якісного його розгляду (s ₃₄ = s ₄₃= 0, s ₂₃ = s ₃₂ за властивістю взаємності та s ₂₃ = - s ₁₃ через протифазність збудження бічних пліч у разі живлення подвійного трійника з боку Е -плеча). Отже,

(1.28)

Запишемо суми парних добутків коефіцієнтів стовпців, поєднаних у правій матриці (1.28) стрілками, відповідно до властивостей унітарності:

звідки випливає

а це може бути тільки для

. (1.29)

З огляду на співвідношення (1.29), симетрію та взаємність розглянутого пристрою

Тепер розглянемо суми квадратів модулів коефіцієнтів двох останніх рядків правої матриці (1.28). За властивістю унітарності,

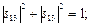
звідси випливає

що й потрібно було довести.

На підставі викладеного, матрицю [ S ] подвійного трійника за належного вибору відлікових перерізів на його входах можна подати у вигляді:

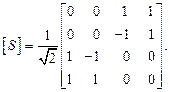(1.30)

Аналогічно матриця [ S ] квадратурного моста має від:

(1.31)

Дата добавления: 2014-11-29