
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Очевидно, что входное сопротивление и проводимость - обратные величины
|
|
|
|
Определим, как связаны реактивное и активное сопротивление с активной и реактивной проводимостью.
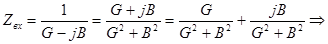
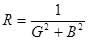 ;
; 
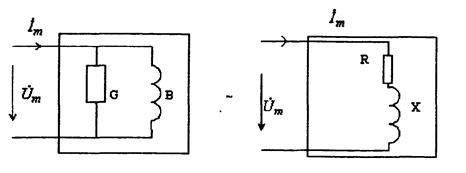
Параллельная схема замещения последовательная схема замещения двухполюсника двухполюсника
Рис.2.21
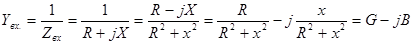
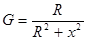 ;
; 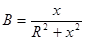 -формулы перехода от последовательной схемы к параллельной
-формулы перехода от последовательной схемы к параллельной
Следует отметить, что зная параметры одной схемы замещения возможно найти параметры другой только при данной частоте, так как в исходной схеме сложной цепи частотные характеристики элементов и ветвей различны.
2.9.Анапиз сложных цепей гармонического тока на основе метода токов связи.
При анализе сложных цепей необходимо от цели, содержащей элементы:
активные сопротивления, емкости, индуктивности, перейти к комплексным сопротивлениям и комплексам амплитудных значений тока и напряжения, затем необходимо перерисовать цепь. Если не обращать внимание на точки и считать, что соответствует R, то для расчета цепей переменного гармонического тока возможно использовать все ранее рассмотренные методы расчета цепей постоянном тока.
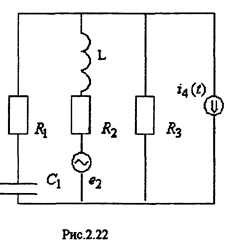
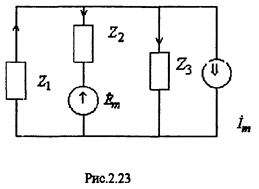
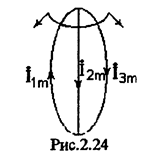
Пример: Составим уравнения для расчета цепи (см. Рис.2.22) по законам Кирхгофа, методом токов связей и узловых напряжений.
|
|
|
|
|
|
Составляем уравнения по МТС:
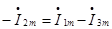
|


Система уравнений (*) содержит только токи ветвей связи, причем это -иначе записанные ЗНК. Правая часть содержит слагаемые с источниками ЭДС и тока, как в ЗНК, а в левой части записаны падения напряжения от токов ветвей связи.
Обозначим Z11, = Z1 + Z2 - собственное сопротивление 1-ого контура, т.е. сумма сопротивлений ветвей, составляющих 1-й контур.
Z31 = Z13 = Z2 - взаимное (общее) сопротивление цепи, общее для 1 -го и третьего контура.
Для к-го контура с учетом введенных обозначений можно записать

Причем если в его ветвях дерева направления обходов к-го и n-го контура разные, то знак "-". При совладении - знак "+".
Особенности: количество уравнений по МТС равно количеству ветвей связи (p-q+1), если нет топологически вырожденных ветвей, содержащих идеальный источник тока.
Nmtc=p-q+1+n,
где n - число идеальных источников тока.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 489; Нарушение авторских прав?; Мы поможем в написании вашей работы!
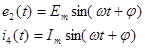

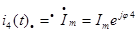

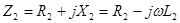

 ;
ЗТК:1к:
;
ЗТК:1к:  3к:
3к: 