Визначення блочних матриць 2 страница

Отже,

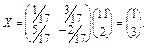
Розв’язок системи: 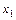= 1; = 3.

Розглянемо однорідну систему лінійних рівнянь:

АХ = 0 (3.34)

Нехай А — квадратна матриця n -го порядку; Х — вектор-стовпець розміру n × 1.

Тривіальний розв’язок має вигляд: 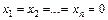. Нетривіальний розв’язок може існувати лише за умови, що визначник матриці А дорівнює нулю:

Коли це так, то система матиме безліч розв’язків. Їх можна нормувати, вимагаючи, наприклад, щоб виконувалася рівність

(3.35)

Приклад 3.6. Знайти нетривіальні розв’язки однорідної системи рівнянь.

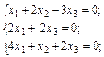(3.36)

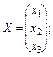
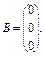
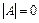, це означає, що задана система має нетривіальні розв’язки.

Матрицю А можна записати як систему трьох векторів:

Систему (3.36) подамо як лінійну комбінацію вектора :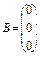

(3.37)

Неважко побачити, що 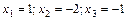; розв’язками системи (3.36) будуть і ці самі значення, помножені на будь-які числа, які задовольняють рівняння (3.37). Отже, система векторів є лінійно залежною, причому розв’язки системи лінійних рівнянь (3.36) є коефіцієнтами лінійної комбінації вектора :

(3.38)

3. 8. Характеристичні (власні) корені
і власні вектори матриць

Розглянемо систему рівнянь

(3.39)

де — скаляр; А — квадратна матриця порядку n, X — розміром n × 1.

Систему (3.39) запишемо у вигляді

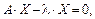
або

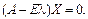(3.40)

Остання система n рівнянь з n невідомими має нетривіальний розв’язок, коли

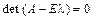або 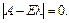(3.41)

Означення 3.21. Рівняння відносно називають характеристичним рівнянням матриці А.

Корені цього рівняння l є характеристичними коренями (характе­ристичними числами, власними значеннями) матриці А.

Візьмемо будь-який корінь характеристичного рівняння (3.41) і підставимо в систему рівнянь (3.40). Дістанемо рівняння

(3.42)

яке має нетривіальний розв’язок, оскільки .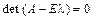

Нехай цим розв’язком є вектор 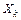. Такий вектор 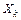є характеристичним, або власним, вектором матриці А, який відповідає характеристичному кореню .

Якщо матриця А має n різних характеристичних коренів, то припускатимемо, що вона має і n різних власних векторів (задачі, які мають кратні характеристичні корені, в економіці зустрічаються рідко).

Власні вектори визначаються з точністю до множення на скаляр. Це не завжди зручно. Тому часто розглядають нормовані власні вектори, тобто такі що:

.

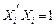Зауважимо, що коли матриця А в рівнянні (3.40) — симетрична (тобто 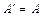), а Х — матриця, кожний стовпець якої є власним вектором цієї матриці, то добуток

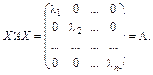(3.43)

Отже, якщо власні вектори матриці А розміщені у вигляді стовпців матриці Х, то добуток 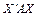перетворює матрицю А на діагональну матрицю, яка має характеристичні корені l на головній діагоналі.

Приклад 3.7. Знайти характеристичні корені матриці А.

Запишемо рівняння або

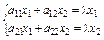
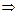
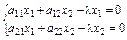
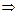
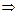
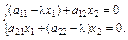(3.44)

Запишемо характеристичне рівняння 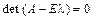для системи (3.44):

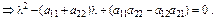(3.45)

Отже,

. (3.46)

Нехай матриця А — симетрична, тоді 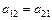і характеристичні корені цієї матриці

. (3.47)

Підставивши поступово в систему (3.44), знайдемо власні вектори X ₁, X ₂ матриці А.

Приклад 3.8. Знайти характеристичні корені і власні вектори X ₁, X ₂ матриці А:

.

Матриця А симетрична. Для визначення застосуємо (3.47):

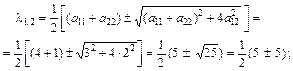
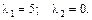
Щоб знайти власні вектори i , розв’яжемо для кожного систему рівнянь (3.44).

Нехай, 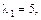тоді

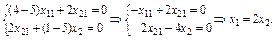(3.48)

Нормалізуємо вектор 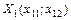, зводячи його довжину до 1, тобто:

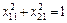(3.49)

Підставимо (3.48) в (3.49):

Звідси,

Власний вектор

(3.50)

Для знаходження власного вектора 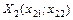покладемо .

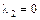Система (3.44) запишеться у вигляді

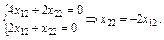(3.51)

Нормалізуємо вектор 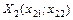, звівши його довжину до 1, тобто:

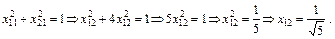(3.52)

Підставивши (3.52) у (3.51), дістанемо:

Власний вектор

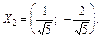(3.53)

Зауважимо, що оскільки 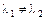, то власні вектори X ₁ і X ₂ ортогональні, тобто лінійно незалежні:

Перевіримо, чи виконується (3.43):

Отже, співвідношення 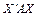справді переводить матрицю А в діагональ­ну матрицю . Це підтверджує правильність наведених обчислень.

3.9. Квадратичні форми

3.9.1. Означення квадратичної форми

Означення 3.22. Квадратичною формою від n невідомих називається сума, кожний доданок якої є квадратом одного з цих невідомих або добутком двох різних невідомих:

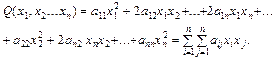(3.54)

Коефіцієнти членів розміщені на головній діагоналі матриці А, а інші елементи матриці симетричні і дорівнюють відповідно половинам коефіцієнтів при :

Симетричну матрицю 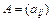називають матрицею квадратичної форми. У векторно-матричній формі квадратична форма має вигляд 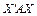, де 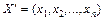, A — симетрична матриця.

Розглянемо, наприклад, два випадки.

1. Матриця А має розмір 2 × 2, а саме . Тоді квадратична форма

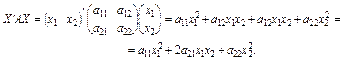
2. Матриця А діагональна, тобто

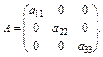
У такому разі

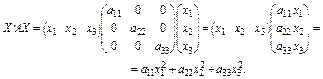
— вагова сума квадратів.

Означення 3.23. Квадратичну форму і відповідну їй матрицю А називають додатно визначеною тоді і тільки тоді, коли 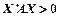для всіх дійсних .

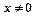Означення 3.24. Квадратичну форму і відповідну їй матрицю називають додатно напіввизначеною, коли для всіх Х.

Запам’ятайте важливу властивість додатно визначених матриць.

Матриця А додатно визначена тоді і тільки тоді, коли її характеристичні корені (власні значення) додатні, а саме:

(3.55)

Рівняння (3.55) можемо пристосувати для знаходження іншого результату, який корисний при вивченні узагальненого методу найменших квадратів.

Оскільки всі додатні, можемо задати діагональну матрицю D такого виду:

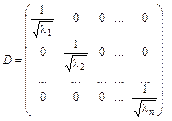(3.56)

Неважко побачити, що добуток (3.55) на матрицю D ліворуч і праворуч дає одиничну матрицю:

(3.57)

Нехай Z = XD, тоді

(3.58)

Оскільки матриці Х і D — невироджені, то Z — також невироджена. Виконавши відповідні перетворення, дістанемо:

(3.59)

Отже, коли матриця А додатно визначена, то можна знайти таку неви­роджену матрицю , що .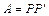

3.9.2. Випадкові квадратичні форми

Нехай d — випадковий вектор, А — детермінована симетрична матриця.

Добуток називають випадковою квадратичною формою, коли коваріаційна матриця d дорівнює 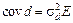і математичне сподівання M (d) = 0.

Застосувавши оператор математичного сподівання до випадкової квадратичної форми , дістанемо:

(3.60)

де tr (A) — слід матриці А.

Наведемо властивості випадкової квадратичної форми.

Означення 3.25. 1. Квадратична форма 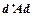має розподіл із k ступенями свободи тоді і тільки тоді, коли А — ідемпотентна матриця (тобто 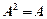) і rgA = trA = k.

2. Нехай В — детермінована матриця, така що BA = 0 і 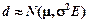. Тод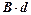і і 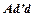— незалежні.

3. Якщо 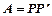— симетрична матриця, то слід матриці А є сумою її власних значень

4. Усі власні значення ідемпотентної матриці А дорівнюють нулю або одиниці, а саме:

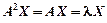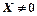якщо то ; проте , тобто , оскільки , то 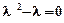. Звідси або .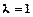

5. Матриця 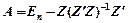є ідемпотентною, rgA = 1 і матриця Z має таку властивість, що ( ) — квадратна симетрична невироджена матриця.

Приклад 3.9. Нехай 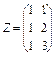; тоді ;

,

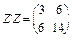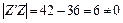отже, матриця — невироджена.

.

Визначимо нову матрицю А так:

.

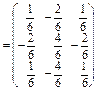Матриця А — симетрична та ідемпотентна, оскільки 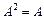. Зауважимо, що ранг матриці А дорівнює 1.

Знайшовши характеристичні корені цієї матриці, тобто розв’язавши рівняння 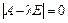, дістанемо 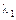= 1 і = 0 кратності 2, що ілюструє виконання властивості 4.

3.10. Диференціювання функції багатьох змінних
(градієнт функціі f (x))

Розглянемо операцію диференціювання функції багатьох змінних f (x ₁ ,x ₂ ... x_n), коли змінні задано у формі матриці-рядка, або, що те саме, вектора, тобто X = (x ₁, x ₂ ... x_n . Тоді можна коротко записати f (x) = (x ₁, x ₂ ... x_n .

Означення 3.25. Градієнтом функції f (x) (позначається: ) називається вектор, який складається з частинних похідних функції f (x) за x ₁, x ₂... x_n:

(3.61)

Нехай потрібно визначити градієнт функції , коли і .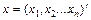

Тоді

.

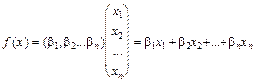Отже, градієнт функції

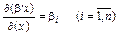. (3.62)

Узявши до уваги, що 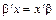, градієнт можна визначити як

. (3.63)

Далі розглянемо функцію 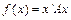, де A = (a_ij) — симетрична матриця порядку n і 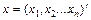— n -вимірна матриця-стовпець. Функцію такого типу визначають як квадратичну форму (див.підрозділ. 3.9).

Визначимо градієнт квадратичної форми. Для цього подамо 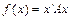як скалярний добуток:

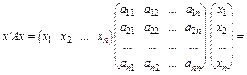
(3.64)

.

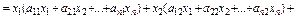
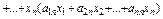Знайдемо компоненти вектора-градієнта.

Перший компонент

.

другий компонент:

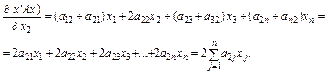
n -й компонент:

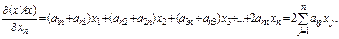
Отже, градієнт від квадратичної форми 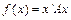має вигляд

(3.65)

Отже, скорочено

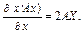(3.66)

3.11. Короткі висновки

1. Матрицею називається таблиця чисел, яка складається з m рядків і n стовпців:

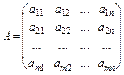
2. Кількість рядків і стовпців матриці визначає її розміпр m × n.

3. Якщо , то матриця — прямокутна; якщо m = n — матриця квадратна порядку n (або m).

4. Якщо матриця має один стовпець або рядок, то її називають відповідно: матрицею-стовпцем або матрицею-рядком. Загалом такі матриці називають векторами, а саме:

5. Якщо матриця А має всі нульові елементи, то вона є нульовою:

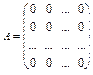
6. Квадратна матриця, усі елементи якої, крім елементів головної діагоналі, дорівнюють нулю, називається діагональною:

7. Якщо в діагональній матриці по головній діагоналі стоять одиниці, а саме

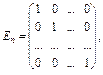
то така матриця називається одиничною n -го порядку.

8. Якщо в матриці 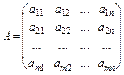поміняти місцями елементи рядків на відповідні елементи стовпців (або навпаки), то дістанемо транспоновану матрицю

9. Квадратна матриця А називається симетричною, якщо .

10. Додавання і віднімання виконується тільки для матриць одного й того самого порядку. Якщо і мають однаковий порядок, то матриця суми (різниці) .

11. Матриця будь-якого порядку А може бути помножена на скаляр l:

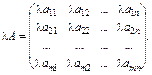
При множенні матриці А на скаляр виконуються такі закони:

а)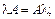

б)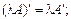

в)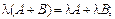

г)

д)

12. Дві матриці А і В можна помножити одна на одну, якщо кількість стовпців першої матриці дорівнює кількості рядків другої матриці. Кожний елемент 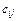матриці-добутку С = АВ є сумою добутків відповідних елементів 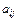і -го рядка на відповідні елементи j -го стовпця:

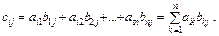
13. При множенні матриць справджуються такі закони:

а) ;

б) (АВ) С = А (ВС);

в) (А + В) С = АС + ВС;

г) С(А + В) = СА + СВ;

д)

е) АE = EA = A;

є)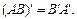

14. Добуток матриці 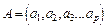на 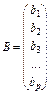дає скаляр

Якщо вектор 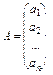, то

і

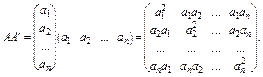
15. Квадратна матриця, що задовольняє умову 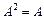, називається ідемпотентною.

16. Кожна матриця має скалярну характеристику — ранг матриці. Рангом називається максимальна кількість лінійно незалежних векторів-стовпців (рядків) матриці А. Існує й інше означення: найвищий порядок мінора матриці А, який відрізняється від нуля:

m, n – кількість відповідно рядків і стовпців матриці А.

17. Якщо rgA = min(m,n), то матриця А має повний ранг. Для рангу виконуються такі співвідношення:

а) rgA = rg ;

б) rg 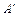A = rgA;

в) rgAB 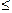min (rgA, rgB).

Дата добавления: 2014-11-29