Визначення блочних матриць 3 страница

г) rg 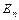= n.

18. Для квадратної матриці існують також скалярні характеристики: слід матриці і її визначник (детермінант).

Слідом матриці розмірности (n × n) є сума елементів, що містяться на її головній діагоналі, тобто

Для сліду виконуються такі співвідношення:

а)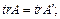

б) (А і В — матриці однакового порядку);

в) tr(AB) = tr(BA);

г) 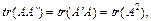(коли А — симетрична);

д)

19. Детермінантом (визначником) квадратної матриці А n -го порядку називається алгебраїчна сума членів, кожний з яких містить n спів­множників, узятих по одному і лише по одному з кожного рядка (стовпця) визначника. Позначається:

det A або .

20. Визначник (n – 1)-го порядку, в якому викреслені і -й рядок і j -й стовпець, називається мінором елемента 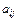і позначається .

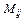21. Мінор 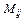, який береться зі знаком , де і — номер рядка,
j — номер стовпця елементa 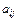, називається алгебраїчним доповненням цього елемента, а саме:

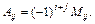
22. Визначник дорівнює сумі попарних добутків елементів будь-якого стовпця (рядка) на їх відповідні алгебраїчні доповнення:

23. Квадратна матриця, для якої 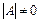, називається невиродженою. Кожна невироджена матриця має єдину обернену матрицю, для якої виконується:

Обернена матриця знаходиться з виразу

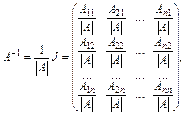
де J — приєднaна матриця.

24. Основні властивості оберненої матриці:

1) ;

2) ;

3) ;

4) ;

5) ;

6) .

25. Матриця, для якої , називається ортогональною.

26. Матриці, в яких елементами є окремі підматриці, називаються блоковими:

Розбиваючи матрицю на підматриці, слід додержувати таких правил:

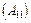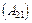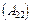— підматриці, що стоять поруч – і – — повинні мати однакову кількість рядків;

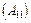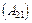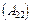— підматриці, які стоять одна під одною – і – — повинні мати однакову кількість стовпців.

27. При додаванні (відніманні) блокових матриць, має насамперед виконуватись умова, що порядок відповідних матриць-доданків однаковий.

При множенні двох блокових матриць кількість стовпців першої матриці має дорівнювати кількості рядків другої матриці. З блоковими матрицями операцію множення виконують за тими самими правилами, що й зі звичайними матрицями.

28. Кронеккеровий добуток двох матриць

де ; .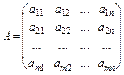

Якщо матриця 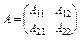блокова, то .

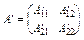29. Обернену блокову матрицю знаходимо за формулою Фробеніуса:

, (3.27)

де ;

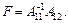
30. Детермінант блокової матриці А

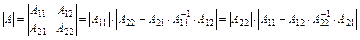
31. Система лінійних рівнянь в матричному вигляді записується АХ = В, дe

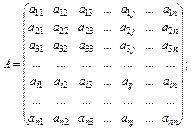
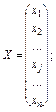
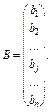
Якщо А — невироджена матриця, то розв’язок системи АХ = В знаходиться як

.

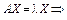
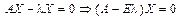32. Система лінійних рівнянь АХ = 0, називається однорідною. Вона має нетривіальні розв’язки, якщо . Система рівнянь має нетривіальний розв’язок, якщо 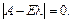Останнє рівняння називають характеристичним рівнянням матриці А.

33. Корені рівняння є характеристичними коренями (характеристичними числами, власними значеннями) матриці А.

34. Вектори X_k, які є розв’язком системи 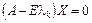для відповідного характеристичного кореня , називаються власними векторами матриці А. Добуток

де Х — матриця власних векторів А;

— характеристичні корені матриці А.

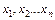35. Квадратична форма від n невідомих записується у вигляді:

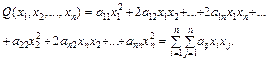
У векторно-матричному запису квадратичну форму можна подати так:

,

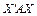де 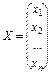, А — симетрична матриця.

36. Якщо d — випадковий вектор, для якого виконується: 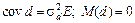, то — називається випадковою квадратичною формою. Для випадкової квадратичної форми

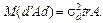
37. Якщо 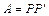— симетрична матриця, то слід матриці А є сумою її власних значень:

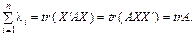
Усі власні значення ідемпотентної матриці А дорівнююють або нулю, або одиниці. Матриця є ідемпотентна, причому ранг її дорівнює 1.

38. Градієнтом функції f (x), коли x = (x ₁, x ₂ ... x_n) є вектор

.

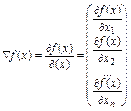39. Якщо функція , то градієнт її

.

40. Градієнт квадратичної форми 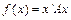дорівнює .

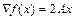3.12. Запитання та завдання для самостійної роботи

1. Задані матриці:

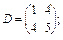
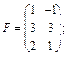
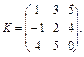
Знайдіть матриці суми (різниці): 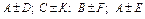. Поясніть, чому не існує суми (різниці) матриць: .

2. Для матриць із завдання 1 знайдіть добутки: BA; CF; CK; AE; DE. Поясніть, чому не існує добутків AB; CD; FC; FB; KA; KE.

3. Для матриць із завдання 1 знайдіть транспоновані до них матриці.

4. Із множини матриць завдання 1 знайдіть симетричні. Яка ознака симетричної матриці?

5. Покажіть, що для матриць із завдання 1 справджується тотожність .

6. Яка матриця називається ідемпотентною? Покажіть, що матриця є ідемпотентною.

7. Назвіть скалярні характеристики матриць.

8. Покажіть, що для матриць А і С із завдання 1 ; .

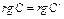9. Дано матрицю 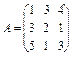. Чому дорівнює слід (tr A) матриці А?

10. Для матриці А із завдання 9 покажіть, що .

11. Дано симетричну матрицю . Покажіть, що .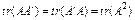

12. Знайдіть визначник матриці А із завдання 11.

13. Для матриці А із завдання 11 покажіть, що .

14. Яка матриця має обернену матрицю? Які з поданих далі матриць мають обернені:

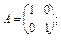
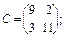
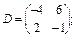
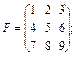
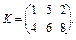
15. Наведіть основні властивості оберненої матриці.

16. Задано матрицю , обернену до матриці А:

.

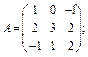
Покажіть, що .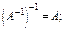

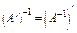17. Покажіть, що матриця

.

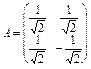є ортогональною.

18. Задана систему лінійних рівнянь

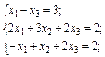
Матриця, обернена до матриці системи,

.

Знайдіть розв’язок даної системи рівнянь.

19. Яка матриця називається блоковою?

20. Задано по чотири блоки блокових матриць А і В:

;

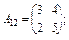
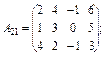
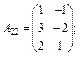
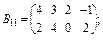
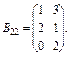
Знайдіть суму (різницю) блокових матриць .

21. Яка умова множення блокових матриць? З відповідних блоків матриць А і В з попереднього завдання складіть дві матриці, які можна було б помножити одна на одну.

22. Задано матриці

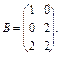
Знайдіть матрицю Кронеккeр-добутку (прямого множення) .

23. Задана блочна невироджена матриця

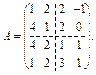
Знайдіть обернену матрицю .

24. Яке рівняння називають характеристичним рівняння матриці А?

25. Яку назву мають корені характеристичного рівняння?

26. Чому дорівнює добуток , де Х — власні вектори матриці А?

27. Знайдіть характеристичні корені і власні вектори матриці:

28. Дайте означення квадратичної форми. Запишіть її у розгорнутому вигляді і в матричній формі.

29. Коли квадратична форма є додатно визначеною і напіввизначеною?

30. Яку квадратичну форму називають випадковою квадратичною формою?

31. Чому дорівнює математичне сподівання випадкової квадратичної форми?

32. Сформулюйте властивості випадкової квадратичної форми.

3.13. Основні терміни і поняття

Матриця Прямокутна матриця Квадратна матриця Транспонована матриця Діагональна матриця Симетрична матриця Одинична матриця Матриця-стовпець Матриця-рядок Ідемпотентна матриця Ранг матриці Слід матриці Детермінант (визначник)

Скаляр Мінор Алгебраїчне доповнення Кронеккерове (пряме) множення матриць Приєднана матриця Обернена матриця Блокова матриця Характеристичне рівняння Характеристичні корені Власні вектори матриці Квадратична форма Випадкова форма

Дата добавления: 2014-11-29