
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Критический анализ моделей
|
|
|
|
Анализ структуры турбулентного потока в пристеночной зоне представляет актуальную задачу для различных отраслей техники. В настоящее время в описании пульсационного движения используют ПРН-модели. Анализ литературы показывает [4], что такие версии весьма успешны в предсказании турбулентных течений. Заметим, что широко используемые в настоящее время двухпараметрические модели [типа (k-e), (k-L), (k-w)] применимы к таким задачам в очень ограниченных случаях и требуют значительной модификации. Данный подход признан бесперспективным. Что касается алгебраических моделей рейнольдсовых напряжений (АМН-моделей), то они вряд ли окажутся универсальными из-за способа построения, опирающегося на допущения об упрощении физического явления.
В связи с этим в настоящей работе поставлены цели: адаптировать различные версии моделей замыкания рейнольдсовых напряжений к оценке развивающихся турбулентных течений в каналах; утвердиться в достоинствах представленных ПРН-моделей в расчете анизотропных пристеночных течений путем сравнения с экспериментальными данными по широкому кругу параметров; оценить замыкающие аппроксимации ПРН-моделей, значения ее численных параметров с целью развить форму модели, рекомендуемую к применению в широкой области технических приложений.
2. Математическая модель течения
Общую систему определяющих уравнений, используемую для расчета развивающихся течений несжимаемой жидкости в каналах, из соображений простоты целесообразно дать в тензорной записи. В этом виде уравнения неразрывности, движения и ПРН-модель [5] выглядят следующим образом:
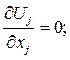 (1)
(1)
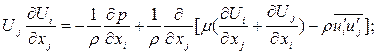 (2)
(2)

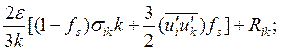 (3)
(3)
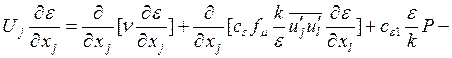
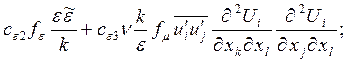 (4)
(4)
Здесь 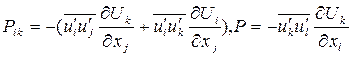 .
.
3. Граничные условия и численный метод решения
Система определяющих уравнений (1)-(4) и замыкающие соотношения записываются в цилиндрической системе координат.
Краевые условия сводятся: к заданию на входе однородных профилей для осевой скорости осредненного течения, нормальных напряжений (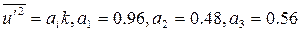 ), кинетической энергии и скорости диссипации (
), кинетической энергии и скорости диссипации (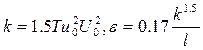 ,где Tu-интенсивность турбулентности), другие параметры в этом случае равны нулю.
,где Tu-интенсивность турбулентности), другие параметры в этом случае равны нулю.
При x= 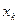 (выход) принято
(выход) принято  На стенке (r=R) реализуются условия прилипания потока и отсутствия турбулентных пульсаций, а также
На стенке (r=R) реализуются условия прилипания потока и отсутствия турбулентных пульсаций, а также 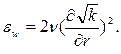 На оси симметрии (r=0):
На оси симметрии (r=0):
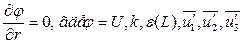 , V=W=0,
, V=W=0, 
Численное интегрирование выполняется на неравномерных сетках. Сгущение узлов к твердым поверхностям отвечает замене переменных в исходных уравнениях:
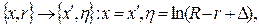
где D-параметр преобразования, обеспечивающий попадание трех- пяти узлов в область  .
.
4. Обсуждение результатов
Расчеты выполнены при следующих параметрах:Re=(0.1¸5)× 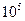 , D=0.007¸0.1м,
, D=0.007¸0.1м, 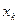 =150D, Tu=(0.4¸10)%, рабочее тело - воздух, вода. Сравнение с данными [1-3,11,12] по параметрам U,
=150D, Tu=(0.4¸10)%, рабочее тело - воздух, вода. Сравнение с данными [1-3,11,12] по параметрам U,  в развивающемся осесимметричном потоке представлено на рис.1-4. Так, на рис.1 изображены распределения относительной скорости
в развивающемся осесимметричном потоке представлено на рис.1-4. Так, на рис.1 изображены распределения относительной скорости 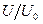 по поперечному сечению в зависимости от y/R (где y=R-r) в различных выделенных сечениях по длине от x/D канала. Линия 1 соответствует x/D=3, 2-12, 3-41. Сплошная линия относится к ПРН-L-модели, линия (----)-модель Элгобаши M3, (¾ ¾) – модель Сима М2, (¾ - - ¾) – модель Ханжалика M1. Значки: - данные опыта Веске (Re=1.6
по поперечному сечению в зависимости от y/R (где y=R-r) в различных выделенных сечениях по длине от x/D канала. Линия 1 соответствует x/D=3, 2-12, 3-41. Сплошная линия относится к ПРН-L-модели, линия (----)-модель Элгобаши M3, (¾ ¾) – модель Сима М2, (¾ - - ¾) – модель Ханжалика M1. Значки: - данные опыта Веске (Re=1.6 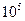 ,D=0.01м, Tu=0.43%, воздух). На рис.2 даны распределения
,D=0.01м, Tu=0.43%, воздух). На рис.2 даны распределения  по длине трубы (x/D) в различных точках по радиальной координате (y/R). Так, линии 1 отвечают y/R =1, 2-0.3, 3-0.15, 4-0.05. Значки – эксперименты (Re=400000, Tu=0.43%, обозначения те же, что и на рис.1). Из рис.1,2 видно, что результаты теории неплохо согласуются с экспериментом. Отличие расчетных данных, полученных по различным моделям незначительно. Это неудивительно,
по длине трубы (x/D) в различных точках по радиальной координате (y/R). Так, линии 1 отвечают y/R =1, 2-0.3, 3-0.15, 4-0.05. Значки – эксперименты (Re=400000, Tu=0.43%, обозначения те же, что и на рис.1). Из рис.1,2 видно, что результаты теории неплохо согласуются с экспериментом. Отличие расчетных данных, полученных по различным моделям незначительно. Это неудивительно,
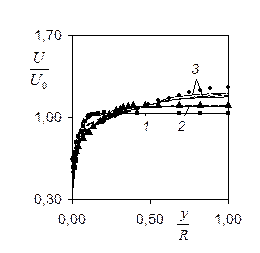 Рис.1
Рис.1
| 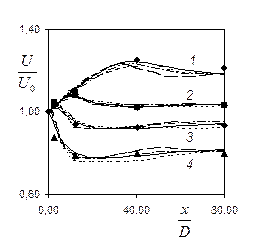 Рис.2
Рис.2
|
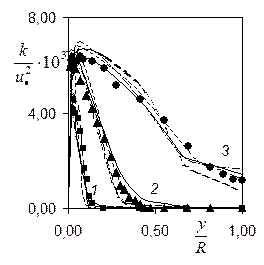 Рис.3
Рис.3
| Рис.1 Профили осевой скорости от поперечной координаты во входной области. Здесь линия – расчет, значки – эксперимент: 1-x./D=3 (■), 2-12 (▲), 3-41 (●); (¾) – ПРН–L, (¾ ¾) – M1, (- - -) – M2, (¾ - - ¾) – M3-модели. Рис.2. Распределения осевой скорости продольной координате в выделенных точках по поперечной координате. Обозначения те же, что и на рис.1, значки – эксперимент: 1-y/R=1 (●), 2-0.3 (■), 3-0.15 (♦), 4-0.05 (▲). Рис.3. Распределение кинетической энергии турбулентности во входной области в зависимости от поперечной координаты. Обозначения те же, что и на рис.1. |
т.к. все они предназначены для расчета развивающихся внутренних течений. Однако, в области 40£x/D£80 как у оси, так и у стенки (рис.2, линии 1,3,4) имеется некоторое рассогласование, связанное с большей чувствительностью (ПРН-e)-моделей к возмущениям, идущим со входа и от стенки. На рис.3 приведены профили кинетической энергии ( )×103 (где
)×103 (где  -динамическая скорость) от y/R в сечениях канала x/D=3, 12, 41 (соответственно линии 1-3). Все обозначения, включая значки, отмечающие эксперимент те же, что и на рис.1. Видно, что наилучшее согласие демонстрирует ПРН-L-модель (сплошная линия). Расчеты показывают, что ни одна из ПРН-e-моделей не предсказывает большой максимум
-динамическая скорость) от y/R в сечениях канала x/D=3, 12, 41 (соответственно линии 1-3). Все обозначения, включая значки, отмечающие эксперимент те же, что и на рис.1. Видно, что наилучшее согласие демонстрирует ПРН-L-модель (сплошная линия). Расчеты показывают, что ни одна из ПРН-e-моделей не предсказывает большой максимум  достаточно точно, что является их общим недостатком в описании течений с малыми числами Рейнольдса. Данные о характере распределений компонентов тензора рейнольдсовых напряжений
достаточно точно, что является их общим недостатком в описании течений с малыми числами Рейнольдса. Данные о характере распределений компонентов тензора рейнольдсовых напряжений 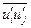 приведены на рис. 4. Значки- результаты опытов [11].
приведены на рис. 4. Значки- результаты опытов [11].
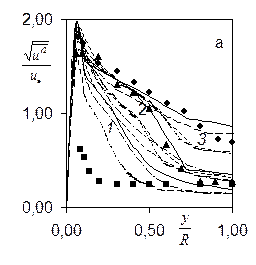
| 
|
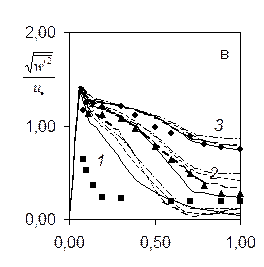
| 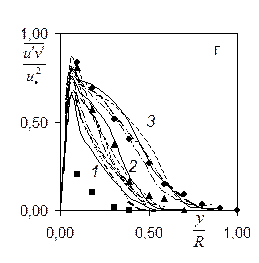
|
Рис.4. Радиальные распределения рейнольдсовых напряжений во входной области. Здесь линия- расчет (обозначения прежние), значки – данные[1,2]: 1-x/D=20 (■), 2-30 (▲), 3-50 (♦), 4-150 (●).
(Re=30000, Re=423500, D=0.1м). Рисунки а)-г) отвечают распределениям  в зависимости от y/R для сечений x/D=20 - линия 1, 30-2, 50-3, 150-4. Все модели удовлетворительно описывают течение в области x/D ³30, однако непосредственно во входной зоне имеется рассогласование. Это связано с ограниченностью экспериментальнах данных: отсутствуют значения e, k,
в зависимости от y/R для сечений x/D=20 - линия 1, 30-2, 50-3, 150-4. Все модели удовлетворительно описывают течение в области x/D ³30, однако непосредственно во входной зоне имеется рассогласование. Это связано с ограниченностью экспериментальнах данных: отсутствуют значения e, k, 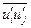 на входе. Из рис.4 видно, что предпочтительнее выглядят модели ПРН-L, ПРН-e (М3). Модель М1 (Ханжалика) весьма груба в определении нормальных компонент у стенки (особенно
на входе. Из рис.4 видно, что предпочтительнее выглядят модели ПРН-L, ПРН-e (М3). Модель М1 (Ханжалика) весьма груба в определении нормальных компонент у стенки (особенно  ). Модель М2 занижает большой максимум на участке стабилизированного течения на 12%, завышает максимум
). Модель М2 занижает большой максимум на участке стабилизированного течения на 12%, завышает максимум 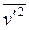 на 40% относительно данных. Отклонение М3 в значениях
на 40% относительно данных. Отклонение М3 в значениях  порядка 8%. Использование L-уравнения [10] в ПРН-модели позволяет наиболее точно раскрыть пристеночную узкую зону течения. Из результатов следует, что отличие моделей в ядре канала незначительно. Это говорит о слабом влиянии способа аппроксимации Rij,2 в данных моделях. У стенки М2, М3 близки, поэтому аппроксимация Rij,w в таких моделях достаточно успешна в описании прямоточных течений. В сравнении с ПРН-L- моделью все модели с e- уравнением имеют недостаток в оценке
порядка 8%. Использование L-уравнения [10] в ПРН-модели позволяет наиболее точно раскрыть пристеночную узкую зону течения. Из результатов следует, что отличие моделей в ядре канала незначительно. Это говорит о слабом влиянии способа аппроксимации Rij,2 в данных моделях. У стенки М2, М3 близки, поэтому аппроксимация Rij,w в таких моделях достаточно успешна в описании прямоточных течений. В сравнении с ПРН-L- моделью все модели с e- уравнением имеют недостаток в оценке  . Последняя характеристика имеет определяющее значение в приcтенном распределении кинетической энергии турбулентности.
. Последняя характеристика имеет определяющее значение в приcтенном распределении кинетической энергии турбулентности.
В качестве иллюстрации возможностей ПРН-L-модели (в пакете Fluent) в расчете конкретного гидродинамического течения слабосжимаемого газа в сложном канале на рис.5(а-е) дана карта “тонких” пульсационных параметров: поля скорости (а), турбулентной кинетической энергии (б), компонент тензора напряжений Рейнольдса (в-е).
 Рис. 5 (а). Поле скорости
Рис. 5 (а). Поле скорости
| 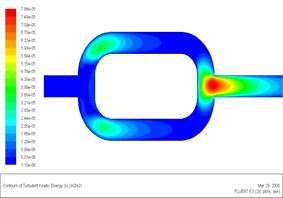 Рис. 5 (б). Поле турбулентной кинетической энергии
Рис. 5 (б). Поле турбулентной кинетической энергии
|
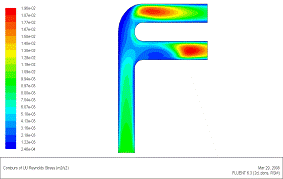 Рис. 5 (в). Осевая нормальная компонента тензора напряжений Рейнольдса
Рис. 5 (в). Осевая нормальная компонента тензора напряжений Рейнольдса
|  Рис. 5 (г) Радиальная нормальная компонента тензора напряжений Рейнольдса
Рис. 5 (г) Радиальная нормальная компонента тензора напряжений Рейнольдса
|
 Рис. 5 (д) Окружная нормальная компонента тензора напряжений Рейнольдса
Рис. 5 (д) Окружная нормальная компонента тензора напряжений Рейнольдса
| 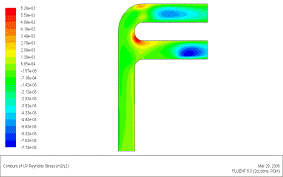 Рис. 5 (е) Напряжение сдвига
Рис. 5 (е) Напряжение сдвига 
|
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 726; Нарушение авторских прав?; Мы поможем в написании вашей работы!