Статистические методы анализа динамики социально-экономических явлений 3 страница

Если стационарный ряд получен по аддитивной модели, сумма всех индексов сезонности должна равняться нулю; если по мультипликативной – числу сезонов.

Метод аналитического выравнивания заключается в подборе функции для описания сезонной волны. Это может быть сделано на основе гармонического анализа, при котором периодическая функция описывается с помощью гармонического ряда Фурье. С помощью данного подхода динамический процесс представляется в виде функции времени, в которой слагаемые расположены по убыванию периодов. Первая гармоника ряда Фурье имеет вид:

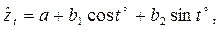
где 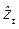- выровненные уровни стационарного ряда;

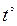- показатель времени, имеющий градусную меру.

Параметры уравнения определяются методом наименьших квадратов. Если данная функция применяется к стационарному ряду, то параметр 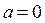. Так как функция периодическая, время в этой модели имеет градусную меру.

В табл. 5.9 представлены исходные и расчетные данные для описания сезонной волны. По условным данным о динамике расхода электроэнергии была описана основная тенденция в виде линейной функции 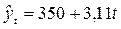, определены остатки первого рода, , для которых и поставлена задача выявления и описания сезонной волны.

Таблица 5.9

Динамика ежеквартального расхода электроэнергии в 2003-2005 гг. (условные данные)

Год	Квартал	Расход э/энергии, тыс. кВт-час	t
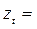
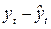
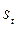
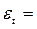
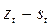
	I		-11	315,77	24,23	22,67	1,56
II		-9	321,99	-11,99	-20,22	8,23
III		-7	328,22	-78,22	-79,78	1,56
IV		-5	334,44	85,56	77,33	8,23
	I		-3	340,66	19,34	22,67	-3,33
II		-1	346,89	-16,89	-20,22	3,33
III			353,11	-73,11	-79,78	6,67
IV			359,34	70,66	77,33	-6,67
	I			365,56	24,44	22,67	1,77
II			371,78	-31,78	-20,22	-11,56
III			378,01	-88,01	-79,78	-8,23
IV			384,23	75,77	77,33	-1,56
Итого				0,00	0,00	0,00

Таблица 5.10

Расчет индексов сезонности

Квартал	Год	Средний остаток (индекс сезонности)
I	24,23	19,34	24,44	22,67
II	-11,99	-16,89	-31,78	-20,22
III	-78,22	-73,11	-88,01	-79,78
IV	85,56	70,66	75,77	77,33
Итого				0,00

Для расчета индексов сезонности, 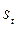, в табл. 5.10 остатки первого рода сгруппированы и усреднены для каждого квартала по трем годам:

…

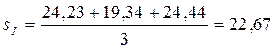Значения индексов сезонности для каждого периода времени внесены в табл. 5.9, после чего рассчитаны остатки второго рода, 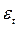, т.е. остатки после вычета двух компонент: тренда и сезонности.

Методы прогнозирования динамики

На основе всестороннего анализа рядов динамики можно оценить будущие значения уровней исследуемых явлений, т.е. составить прогноз. Применение статистических методов прогнозирования основано на предположении о том, что выявленная закономерность развития ряда динамики сохранится и в будущем, т.е. прогноз основывается на экстраполяции. Точность прогноза напрямую зависит от оправданности данных предположений.

Чем больше интервал прогнозирования, тем менее надежна простая экстраполяция. Рекомендуется, чтобы дальность прогноза не была больше 1/3 продолжительности ретроспективного периода.

База экстраполяции (продолжительность ретроспективного периода) также влияет на точность прогноза: слишком короткая может не отражать типичные черты развития, слишком длинная – затушевывать последние сложившиеся тенденции. Таким образом, оптимальная продолжительность должна определяться на основе теоретического анализа сущности явления.

Различают следующие методы прогнозирования: наивные, или простейшие (по среднему абсолютному приросту или среднему коэффициенту роста), и по уравнению тренда.

Простейший метод прогнозирования по среднему абсолютному приросту основан на предположении о стабильности абсолютных приростов в будущем. Данный метод может использоваться, если имеются основания считать общую тенденцию развития линейной. Таким образом, прогнозируемый на определенный момент/период уровень ряда динамики определяется по формуле:

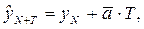
где 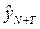- экстраполируемый на момент/период (N+T) уровень;

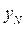- конечный уровень ретроспективного периода;

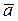- средний абсолютный прирост за ретроспективный период;

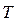- срок прогноза.

Простейший метод прогнозирования по среднему коэффициенту роста предполагает стабильность коэффициентов роста в будущем. Это обосновано, если есть основания считать общую тенденцию экспоненциальной (показательной). прогнозируемый уровень в данном случае определяется по формуле:

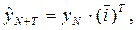
где 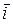- средний коэффициент роста за ретроспективный период.

Наивные методы прогнозирования, являясь простейшими, являются и наиболее приближенными.

Метод прогнозирования по уравнению тренда основан на использовании тенденции, описанной для ретроспективного периода. При этом точечный прогноз по трендовой модели дополняется доверительными интервалами:

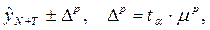
где 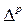- предельная ошибка прогноза;

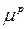- средняя ошибка прогноза;

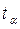- табличное значение t – критерия Стьюдента.

Помимо экстраполяции иногда прибегают к интерполяции – определению неизвестных уровней внутри ряда динамики. Интерполяция может производиться на основе тех же методов, что и экстраполяция. При этом исходят из допущения, что выявленная тенденция существенно не менялась в том временном отрезке, уровни которого неизвестны.

Контрольные вопросы

1. Раскройте понятия динамики, ряда динамики и его компонент.

2. Какие виды рядов динамики различают?

3. Каковы основные правила построения ряда динамики?

4. Раскройте проблему сопоставимости уровней ряда динамики.

5. Назовите приемы для достижения сопоставимости уровней ряда динамики.

6. Какие индивидуальные показатели динамики вы знаете?

7. Какие сводные показатели динамики вы знаете?

8. Чем определяется порядок усреднения уровней ряда динамики?

9. Каковы основные компоненты ряда динамики?

10. В чем состоят различия сезонных и циклических колебаний?

11. Чем определяется выбор аддитивной или мультипликативной модели ряда динамики?

12. Какие методы выявления и описания основной тенденции вам известны?

13. Какова разница между механическим и аналитическим выравниванием?

14. Какие приемы могут быть использованы для выбора вида уравнения тренда?

15. Какие методы выявления и описания сезонных колебаний вам известны?

16. Какие методы прогнозирования вам известны?

Дата добавления: 2014-11-29