Статистические методы анализа динамики социально-экономических явлений 2 страница

Средний абсолютный прирост показывает, на сколько в среднем увеличивался или уменьшался уровень ряда по сравнению с предыдущим за единицу времени за весь анализируемый период.

Средний коэффициент роста, - обобщающий показатель, характеризующий среднюю интенсивность изменения. То есть, это такой показатель, что если в единицу времени уровень ряда будет последовательно расти (снижаться) в раз в единицу времени, то начиная с первого уровня, за то же число периодов достигнет конечного. Ведущий показатель в данном случае представляет собой произведение цепных коэффициентов роста, т.е. базисный коэффициент роста. Таким образом, средний коэффициент роста определяется как среднее геометрическое из цепных коэффициентов роста:

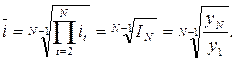
Средний коэффициент роста показывает, во сколько раз в среднем изменялся уровень ряда динамики по сравнению с предыдущим за единицу времени за весь анализируемый период.

Средний темп роста, - это средний коэффициент роста, выраженный в процентах:

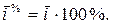
Средний темп роста показывает, сколько процентов в среднем за единицу времени составлял уровень ряда динамики от предыдущего за весь анализируемый период.

Средний коэффициент прироста, - обобщающий показатель, характеризующий среднюю относительную скорость изменения. Данный показатель не определяется непосредственным усреднением цепных коэффициентов прироста, а находится через средний коэффициент роста:

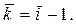
Средний коэффициент прироста показывает, на какую долю в среднем изменялся уровень ряда динамики по сравнению с предыдущим за единицу времени за весь анализируемый период.

Средний темп прироста, - это средний коэффициент прироста, выраженный в процентах:

Средний темп прироста показывает, на сколько процентов в среднем изменялся уровень ряда динамики по сравнению с предыдущим за единицу времени за весь анализируемый период.

Средние показатели изменения уровней ряда, представленного в табл. 5.5, будут следующими.

Средний абсолютный прирост:

,

т.е. в период 2004-2008 гг. общая площадь приватизируемых помещений сокращалась ежегодно в среднем на 9,5 млн. м².

Средний коэффициент и темп роста:

,

,

т.е. в период 2004-2008 гг. годовая общая площадь приватизируемых помещений сокращалась и составляла в среднем 0,82 от общей площади помещений, приватизированных в предыдущем году, или 82%.

Средний коэффициент и темп прироста:

,

,

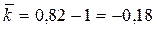т.е. в период 2004-2008 гг. годовая общая площадь приватизируемых помещений сокращалась в среднем на 0,18 от общей площади помещений, приватизированных в предыдущем году, или на 18%.

Компоненты ряда динамики. Методы выравнивания ряда динамики

Исследование рядов динамики не ограничивается изучением скорости и интенсивности развития динамических процессов с помощью системы показателей. Большой интерес представляет изучение закономерностей изменения уровней ряда во времени.

На ряд динамики могут воздействовать факторы эволюционного, осциллятивного и случайного характера.

Общее направление развития (эволюция) динамического процесса определяется факторами эволюционного характера, действующими на ряд динамики практически постоянно. При этом об изменениях значений уровней ряда говорят как о тенденции развития.

Основная тенденция развития, или тренд, - это общее направление развития (рост, снижение или стабилизация) процесса с течением времени.

Факторы осциллятивного характера, действуя на ряд динамики периодически и кратковременно, вызывают, соответственно, циклические (конъюнктурные) и сезонные колебания.

Циклические (конъюнктурные) колебания – это долговременные регулярные колебания, вызванные постоянно действующими факторами (например, циклы экономической конъюнктуры). Их воздействие схематически походит на синусоиду: значение признака за определенное время достигает максимума, затем – минимума, потом вновь возрастает и т.д.

Сезонные колебания – это периодические колебания, повторяющиеся в определенное время года, дни месяца, часы суток.

Факторы случайного характера, действуя несистематически, вызывают нерегулярные колебания то в одном, то в другом направлении. Эти явления делят две группы: вызывающие спорадические (война, экологическая катастрофа) и случайные, второстепенные изменения.

Исходя из вышеописанной классификации факторов, воздействующих на динамические процессы, для целей анализа в рядах динамики выделяют четыре основные компоненты:

Компоненты ряда динамики связаны между собой. В зависимости от характера этой взаимосвязи различают аддитивную и мультипликативную модели рядов динамики.

Для аддитивной модели вида характерны постоянные амплитуды циклических и сезонных колебаний на протяжении всего ряда динамики.

В мультипликативной модели вида циклические и сезонные колебания образуются с переменной амплитудой.

Построение модели динамического процесса сводится к его «разложению» на компоненты с расчетом их значений для каждого уровня ряда динамики.

Методы выявление основной тенденции в рядах динамики

Под колеблемостью в динамических рядах понимаются отклонения уровней ряда от основной тенденции (тренда).

Тренд – это компонента ряда динамики, характеризующая основную долговременную тенденцию изменения его уровней. Обычно тренд описывают гладкой функцией.

Для описания тенденции используют методы механического и аналитического выравнивания.

Суть методов механического выравнивания заключается в замене фактических уровней ряда расчетными, для которых характерна меньшая степень колеблемости. К данным методам относятся методы: усреднения по левой и правой половине, укрупнения интервалов, скользящих средних.

Метод усреднения по левой и правой половине подразумевает разделение ряда на две равные части с последующим расчетом средних уровней для каждой половины. Через рассчитанные средние значения проводится прямая, характеризующая линию тренда на графике. Данный метод очень грубый и позволяет описать тренд только уравнением прямой.

Метод укрупнения интервалов заключается в замене ряда динамики другим, уровни которого относятся к более продолжительным периодам времени. Переход к новым значениям признака для более продолжительных периодов осуществляется либо путем суммирования, либо через усреднение уровней предыдущего ряда. Если уровни колеблются с определенной периодичностью, то для устранения влияния таких колебаний укрупненный интервал желательно взять равным длине «волны». Данный метод позволяет более четко «разглядеть» основную тенденцию в изучаемом процессе.

Метод скользящей средней заключается в последовательном (со сдвигом на один уровень) объединении внутри ряда динамики нескольких уровней и расчете для таких локальных периодов их средних уровней.

Интервал сглаживания – это целое число уровней, которые объединяются в локальный период и для которых рассчитывается средний уровень. Интервал сглаживания может быть нечетным и четным.

Звено скользящей средней – это средний уровень за выбранный интервал сглаживания. Каждое звено скользящей средней относят к середине локального периода.

Для нечетного интервала сглаживания значения скользящей средней определяются по формуле:

где - выровненный уровень (скользящее среднее);

- интервал сглаживания (нечетный).

При четном интервале сглаживания каждое звено скользящей средней должно относиться к середине между центральными датами локального интервала. Для ликвидации такого сдвига применяют способ центрирования. Он заключается в усреднении смежных звеньев скользящей средней и отнесении полученного результата к определенной дате (середине между смежными звеньями).

Использование метода скользящей средней позволяет сгладить ряд с сильными колебаниями. Необходимо отметить, что с увеличением интервала увеличивается и эффект сглаживания, но при этом растет и число «потерянных» значений, т.е. ряд укорачивается на 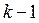значений.

Также к недостаткам метода можно отнести отсутствие аналитического выражения для основной тенденции, что неудобно для целей прогнозирования. Вместе с тем, метод скользящей средней широко используется на первом этапе построения моделей динамики.

В табл. 5.6 приведены исходные и расчетные данные, иллюстрирующие методы механического выравнивания.

Графики исходных данных и выровненных рядов представлены на рис. 5.1.

Таблица 5.6

Динамика объема продаж условного товара за 1995-2009 гг. и механическое выравнивание уровней

№ уровня	Год	Объем продаж, млн. шт./год	Средняя за пять лет	Скользящая средняя (интервал 3 года)	Скользящая средняя (интервал 5 лет)
			4,0	-	-
			3,0	-
			3,3	4,0
			5,3	5,2
			6,0	5,6
			11,2	7,0	7,4
			8,7	9,4
			10,3	11,2
			14,7	12,4
			14,3	16,4
			24,2	18,7	18,4
			20,7	22,0
			26,3	24,2
			27,7	-
			-	-

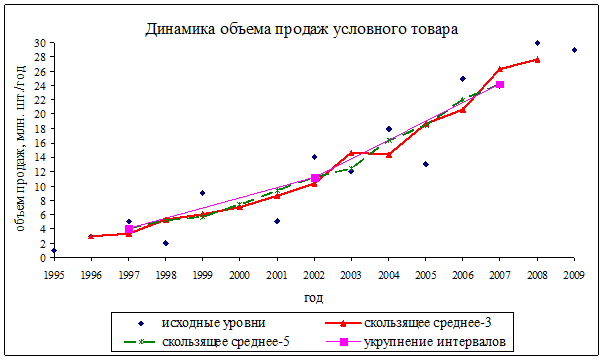
Рис. 5.1. Динамика объема продаж условного товара. Механическое выравнивание.

Видно, что изначально сильно варьирующие данные после выравнивания проявляют более четкую тенденцию. В методе скользящей средней выравнивание тем больше, чем больше интервал сглаживания, однако, это сопровождается потерей большего количества уровней.

Метод аналитического выравнивания состоит в подборе функции для описания зависимости уровней ряда от времени, которая в определенном отношении была бы наиболее близка к фактическим значениям уровней ряда динамики.

Аналитическое выравнивание подразумевает последовательную реализацию трех этапов: подбор вида аналитического уравнения (т.е. формы кривой), расчет параметров выбранной функции, расчет теоретических (т.е. по модели) значений уровней ряда и анализ полученной модели.

Вид уравнения тренда определяется сущностью исследуемого процесса. На практике такой подбор чаще всего основывается на графическом анализе фактических уровней ряда динамики или их сглаженных значений. При этом могут использоваться различные уравнения: полиномы разной степени, логистические кривые, экспоненты и др.

Если основная тенденция хорошо описывается несколькими видами функций, выбирают более простую. Это непосредственно связано с надежностью оцениваемых параметров, так как с увеличением количества параметров уравнения эта надежность снижается и, одновременно, растут ошибки оценки параметров функции и будущих прогнозов.

При выборе вида функции может использоваться метод конечных разностей. Для применения данного метода уровни ряда должны быть равноотстоящими.

Разности первого порядка представляют собой цепные абсолютные приросты:

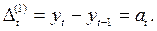
Разности второго порядка равны разности между текущим и предыдущим значениями разностей первого порядка, т.е. представляют собой абсолютные ускорения:

Разности j -го порядка равны разности между текущим и предыдущим значениями разностей (j-1) -го порядка:

Анализ конечных разностей позволяет выбрать степень полинома в соответствующей модели динамики:

где - выровненный уровень (теоретическое значение);

- степень полинома.

При постоянстве разностей j -го порядка рекомендуется использовать полином j -й степени. Преимущество полиномов невысоких степеней состоит в возможности конкретной интерпретации их параметров. Параметр характеризует средние условия образования уровней ряда динамики, а параметры 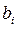- изменения ускорения.

Таким образом, если разности первого порядка приблизительно равны друг другу, это свидетельствует о том, что уровни ряда изменяются приблизительно в арифметической прогрессии. В данном случае рекомендуется полином первой степени, т.е. прямая:

Линейный характер динамики встречается довольно часто. Параметр называется коэффициентом регрессии и интерпретируется как средний абсолютный прирост за единицу времени, т.е. показывает, на сколько в среднем изменится уровень ряда при изменении времени на единицу. Знак коэффициента регрессии определяет направление развития: при - к равномерному росту, при 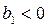- к равномерному снижению.

Если примерно постоянны разности второго порядка (ускорения), то рекомендуется полином (парабола) второй степени:

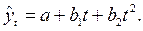
Парабола второго порядка хорошо описывает динамические процессы, для которых характерно изменение направления развития: со снижения - к росту, и наоборот. При этом выражает начальную скорость роста, а - постоянную скорость изменения прироста (абсолютное ускорение).

Теоретически любой ряд динамики может быть абсолютно точно описан полиномом. Однако, параболы выше третьего порядка на практике не используются не только из-за снижения надежности оценок параметров, но и из-за нивелирования сути тренда как отражения основной тенденции: парабола, проходящая через все точки ряда динамики смешивает основную тенденцию с колебаниями.

Кроме метода конечных разностей, для выбора конкретного вида функции используют анализ самого процесса.

Если цепные коэффициенты роста оказываются примерно одинаковыми, это свидетельствует об изменении уровней согласно геометрической прогрессии. В данном случае выравнивание можно произвести по показательной и экспоненциальной функции:

Экспоненциальный характер основной тенденции свойственен процессам, потенциально не имеющим ограничений для роста. Но на практике это возможно лишь на ограниченном промежутке времени. Параметр 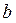(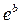) в данных моделях интерпретируется как средний коэффициент роста.

Для убывающих процессов, в которых значения исследуемого признака стремятся, но не могут достичь, с одной стороны нуля, с другой – некоторого предела, используется гиперболическая функция:

Для процессов, проходящих полный цикл развития: возрастание с ускорением в начале, стабилизация в середине и затухание в конце при приближении к предельному уровню, - применяют логистическую функцию.

Расчет параметров выбранной функции тренда может производиться различными способами: по известным уровням ряда динамики, методом линейных отклонений, методом конечных разностей, методом наименьших квадратов. Первые два метода могут применяться лишь для ориентировочных расчетов.

Чаще всего на практике используется метод наименьших квадратов, предполагающий определение параметров выбранной функции, при которых сумма квадратов отклонений фактических уровней ряда динамики от соответствующих по времени выровненных уровней будет минимальна:

Параметры функции, удовлетворяющие данному условию, находятся решением системы нормальных уравнений. При этом вид системы уравнений и, соответственно, ее решение значительно упрощается, если исходную временную шкалу, представленную рядом натуральных чисел (1,2,…), заменить преобразованной, для которой сумма показателей времени равна нулю.

Переход к новой шкале при нечетном числе уровней ряда осуществляется переносом начала отсчета времени (нуля) в середину, приписывая его центральному уровню ряда:

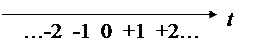
При четном числе уровней ряда начало отсчета времени находится между двумя центральными уровнями, а показатели времени нумеруются нечетными числами:

…-5 -3 -1 +1 +3 +5…

Тогда система нормальных уравнений принимает вид:

- для прямой

- для параболы второго порядка

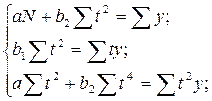
- для экспоненты

- для гиперболы

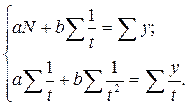
После определения параметров уравнения тренда для ряда динамики рассчитываются теоретические значения уровней (т.е. соответствующие функции тренда) и анализируются их отклонения от фактических уровней ряда динамики, характеризующие ошибки тренда. Как и в классических регрессионных моделях, описанных с помощью МНК, в качестве меры точности найденной функции используют коэффициент детерминации:

где 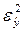- остаточная дисперсия;

- общая дисперсия.

Данные табл. 5.6 и их графическое изображение (рис. 5.1.) позволяют предположить наличие линейной или параболической основной тенденции. Для нахождения аналитического выражения тренда перейдем к новой временной шкале. Необходимые данные для расчета параметров линейного и параболического (второго порядка) трендов приведены в табл. 5.7.

Таблица 5.7

Динамика объема продаж условного товара и определение параметров уравнения тренда МНК

Год	Объем продаж, млн. шт./год	t	t^2	yt	t^4	yt^2	y^2
		-7		-7
		-6		-18
		-5		-25
		-4		-8
		-3		-27
		-2		-14
		-1		-5
Итого

Тогда система нормальных уравнений принимает вид:

- для прямой

- для параболы второго порядка

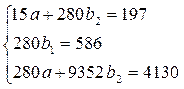
Решая системы, получаем следующие уравнения тренда:

- для прямой

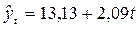
- для параболы второго порядка

.

Графическое изображение полученных линий тренда представлено на рис. 5.2.

Рис. 5.2. Динамика объема продаж условного товара. Аналитическое выравнивание.

Для оценки найденных уравнений тренда в табл. 5.8 рассчитаны значений объема продаж по каждому регрессионному уравнению и ошибки трендов.

Используя данные об ошибках регрессионных значений, рассчитаем коэффициенты детерминации:

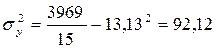
- для прямой

- для параболы второго порядка

.

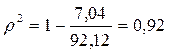Оба уравнения тренда достаточно хорошо описывают основную тенденцию динамики объема продаж.

Таблица 5.8

Регрессионные значения объема продаж

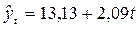
t	Объем продаж, млн. шт./год	Линейный тренд	Параболический тренд
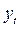
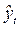
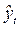
-7		-1,52	6,33	1,81	0,66
-6		0,58	5,87	2,48	0,27
-5		2,67	5,43	3,36	2,68
-4		4,76	7,63	4,47	6,10
-3		6,85	4,60	5,79	10,28
-2		8,95	3,79	7,34	0,11
-1		11,04	36,49	9,10	16,83
		13,13	0,75	11,09	8,50
		15,23	10,41	13,29	1,66
		17,32	0,46	15,71	5,25
		19,41	41,11	18,35	28,64
		21,50	12,22	21,21	14,35
		23,60	0,16	24,29	0,09
		25,69	18,57	27,59	5,80
		27,78	1,48	31,11	4,46
Итого		197,00	155,32	197,00	105,65
В среднем	13,13	13,13	10,35	13,13	7,04

После описания основной тенденции ряда динамики она исключается путем последовательного вычитания из фактических уровней их выровненных значений (для аддитивной модели) или путем деления фактических уровней на теоретические (для мультипликативной модели). Таким образом, в результате исключения тренда, образуется стационарный ряд динамики, или ряд остатков первого рода, для которого можно поставить задачу выявления и описания сезонных колебаний.

Методы выявления сезонных колебаний в рядах динамики

Сезонные колебания обычно связаны со сменой времен года и повторяются регулярно с интервалом в один год. Поэтому для выявления устойчивой сезонной волны необходим анализ распределенных по месяцам (кварталам, декадам) данных за несколько лет (не менее трех).

Для оценки сезонных колебаний (сезонных волн) могут быть использованы следующие методы: абсолютных или относительных разностей, построения индексов сезонности, аналитического выравнивания.

Метод расчета индексов сезонности основан на построении аналитической группировки. Для этого остатки первого рода группируются по периодам/моментам времени внутри года (по месяцам, кварталам, декадам). Затем для каждого периода/момента вычисляется среднее значение стационарного ряда за имеющееся число лет. Набор этих значений можно рассматривать как индексы сезонности, которые описывают сезонную волну.

Дата добавления: 2014-11-29