Отношение эквивалентности

Примеры отношений

Бинарные отношения (отношения степени 2)

В математике большую роль играют бинарные отношения, т.е. отношения, заданные на декартовом произведении двух множеств .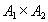

Определение 8. Отношение 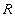на множестве 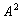называется отношением эквивалентности, если оно обладает следующими свойствами:

1. 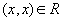для всех 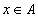(рефлексивность)

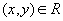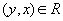2. Если , то (симметричность)

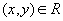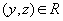3. Если и , то 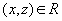(транзитивность)

Обычно отношение эквивалентности обозначают знаком 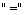или 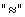и говорят, что оно (отношение) задано на множестве 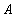(а не на 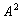). Условия 1-3 в таких обозначениях выглядят более естественно:

1. 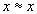для всех 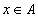(рефлексивность)

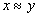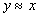2. Если , то (симметричность)

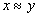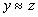3. Если и , то 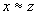(транзитивность)

Легко доказывается, что если на множестве 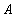задано отношение эквивалентности, то множество 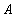разбивается на взаимно непересекающиеся подмножества, состоящие из эквивалентных друг другу элементов (классы эквивалентности).

Пример 1. Рассмотрим на множестве вещественных чисел 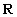отношение, заданное просто равенством чисел. Предикат такого отношения:

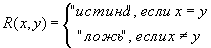, или просто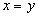

Условия 1-3, очевидно, выполняются, поэтому данное отношение является отношением эквивалентности. Каждый класс эквивалентности этого отношения состоит из одного числа.

Пример 2. Рассмотрим более сложное отношение эквивалентности. На множестве целых чисел 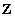зададим отношение "равенство по модулю n" следующим образом: два числа 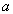и 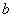равны по модулю n, если их остатки при делении на n равны. Например, по модулю 5 равны числа 2, 7, 12 и т.д.

Условия 1-3 легко проверяются, поэтому равенство по модулю является отношением эквивалентности. Предикат этого отношения имеет вид:

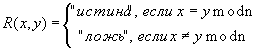
Классы эквивалентности этого отношения состоят из чисел, дающих при делении на n одинаковые остатки. Таких классов ровно n:

[0] = {0, n, 2n, …}[1] = {1, n+1, 2n+1, …}…[n-1] = {n-1, n+n-1, 2n+n-1, …}

Дата добавления: 2014-11-29