Еще пример бинарного отношения

Функциональное отношение

Определение 10. Отношение 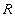на декартовом произведении двух множеств 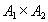называется функциональным отношением, если оно обладает следующим свойством:

1. Если 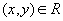и , то 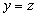(однозначность функции).

Обычно, функциональное отношение обозначают в виде функциональной зависимости - 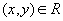тогда и только тогда, когда 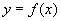. Функциональные отношения (подмножества декартового произведения!) называют иначе графиком функции или графиком функциональной зависимости.

Предикат функционального отношения есть просто выражение функциональной зависимости .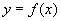

Пример 5. Пусть множество 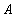есть следующее множество молодых людей: {Вовочка, Петя, Маша, Лена}, причем известны следующие факты:

1. Вовочка любит Вовочку (эгоист).

2. Петя любит Машу (взаимно).

3. Маша любит Петю (взаимно).

4. Маша любит Машу (себя не забывает).

5. Лена любит Петю (несчастная любовь).

Информацию о взаимоотношения данных молодых людей можно описать бинарным отношением "любить", заданном на множестве 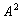. Это отношение можно описать несколькими способами.

Способ 1. Перечисление фактов в виде произвольного текста (как это сделано выше).

Способ 2. В виде графа взаимоотношений:

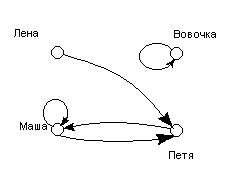
Рисунок 1 Граф взаимоотношений

Способ 3. При помощи матрицы взаимоотношений:

Кого Кто	Вовочка	Петя	Маша	Лена
Вовочка	Любит
Петя			Любит
Маша		Любит	Любит
Лена		Любит

Таблица 1. Матрица взаимоотношений

Способ 4. При помощи таблицы фактов:

Кто любит	Кого любят
Вовочка	Вовочка
Петя	Маша
Маша	Петя
Маша	Маша
Лена	Петя

Таблица 2 Таблица фактов

С точки зрения реляционных баз данных наиболее предпочтительным является четвертый способ, т.к. он допускает наиболее удобный способ хранения и манипулирования информацией. Действительно, перечисление фактов как текстовая форма хранения информации уместна для литературного произведения, но с трудом поддается алгоритмической обработке. Изображение в виде графа наглядно, и его удобно использовать как конечную форму представления информации для пользователя, но хранить данные в графическом виде неудобно. Матрица взаимоотношений уже больше соответствует требованиям информационной системы. Матрица удобна в обработке и компактно хранится. Но одно небольшое изменение, например, появился еще Вася и влюбился в несчастную Лену, требует перестройки всей матрицы, а именно, добавления и колонок, и столбцов. Таблица фактов свободна от всех этих недостатков - при добавлении новых действующих лиц просто добавляются новые строки.

Что касается предиката данного отношения, то он имеет следующий вид (дизъюнктивная нормальная форма):

R(x,y) = {(x = "Вовочка" AND y = "Вовочка") OR (x = "Петя" AND y = "Маша") OR (x = "Маша" AND y = "Петя") OR (x = "Маша" AND y = "Маша") OR (x = "Лена" AND y = "Петя")}

Замечание. Приведенное отношение не является ни транзитивным, ни симметричным или антисимметричным, ни рефлексивным, поэтому оно не является ни отношением эквивалентности, ни отношением порядка, ни каким-либо другим разумным отношением.

Замечание. Большая часть мировой литературы существует и имеет смысл лишь постольку, поскольку бинарное отношение "любить" не является отношением эквивалентности. В частности, по этой причине человечество не разбивается на классы эквивалентности взаимно любящих особей. Изучением характеристик данного отношения и соответствующего ему предиката занималось (и продолжает заниматься) большое количество экспертов, таких как Толстой Л.Н., Шекспир В. и др.

n-арные отношения (отношения степени n)

В математике n-арные отношения рассматриваются относительно редко, в отличие от баз данных, где наиболее важными являются именно отношения, заданные на декартовом произведении более чем двух множеств.

Пример 6. В некотором университете на математическом факультете учатся студенты Иванов, Петров и Сидоров. Лекции им читают преподаватели Пушников, Цыганов и Шарипов, причем известны следующие факты:

1. Пушников читает лекции по алгебре и базам данных, соответственно, 40 и 80 часов в семестр.
2. Цыганов читает лекции по геометрии, 50 часов в семестр.
3. Шарипов читает лекции по алгебре и геометрии, соответственно, 40 и 50 часов в семестр.
4. Студент Иванов посещает лекции по алгебре у Шарипова и по базам данных у Пушникова.
5. Студент Петров посещает лекции по алгебре у Пушникова и по геометрии у Цыганова.
6. Студент Сидоров посещает лекции по геометрии у Цыганова и по базам данных у Пушникова.

Для того чтобы формально описать данную ситуацию (например, в целях разработки информационной системы, учитывающей данные о ходе учебного процесса), введем три множества:

• Множество преподавателей 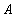= {Пушников, Цыганов, Шарипов}.
• Множество предметов 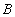= {Алгебра, Геометрия, Базы данных}.
• Множество студентов 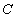= {Иванов, Петров, Сидоров}.

Имеющиеся факты можно разделить на две группы. 1 группа (факты 1-3) - факты о преподавателях, 2 группа (факты 4-6) - факты о студентах.

Для того чтобы отразить факты 1-3 (характеризующие преподавателей и читаемые ими лекции), введем отношение 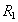на декартовом произведении 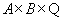, где 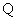- множество рациональных чисел. А именно, упорядоченная тройка 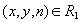тогда и только тогда, когда преподаватель 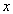читает лекции по предмету 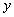в количестве 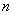часов в семестр. Назовем такое отношение "Читает лекции по…". Множество кортежей, образующих отношение 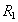удобно представить в виде таблицы:

A (Преподаватель)	B (Предмет)	Q (Количество часов)
Пушников	Алгебра
Пушников	Базы данных
Цыганов	Геометрия
Шарипов	Алгебра
Шарипов	Геометрия

Таблица 3 Отношение "Читает лекции по…"

Для того чтобы отразить факты 4-6 (характеризующие посещение студентами лекций), введем отношение 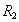на декартовом произведении 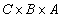. Упорядоченная тройка 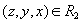тогда и только тогда, когда студент 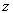посещает лекции по предмету 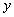у преподавателя 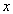. Назовем это отношение "Посещать лекции". Его также представим в виде таблицы:

C (студент)	B (предмет)	A (Преподаватель)
Иванов	Алгебра	Шарипов
Иванов	Базы данных	Пушников
Петров	Алгебра	Пушников
Петров	Геометрия	Цыганов
Сидоров	Геометрия	Цыганов
Сидоров	Базы данных	Пушников

Таблица 4 Отношение "Посещать лекции"

Рассмотрим отношение 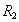подробнее. Оно задано на декартовом произведении 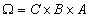. Это произведение, содержащее 3*3*3=27 кортежей, можно назвать "Студенты-Лекции-Преподаватели". Множество 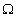представляет собой совокупность всех возможных вариантов посещения студентами лекций. Отношение же 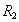показывает текущее состояние учебного процесса. Очевидно, что отношение 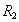является изменяемым во времени отношением.

Итак, факты о ходе учебного процесса удалось отразить в виде двух отношений третьей степени (3-арных), а сами отношения изобразить в виде таблиц с тремя колонками.

Удобство использования табличной формы для задания отношения определяется в данном случае следующими факторами:

1. Все используемые множества конечны.
2. При добавлении или удалении студентов, предметов, преподавателей просто добавляются или удаляются соответствующие строки в таблице.

Нас сейчас не интересует вопрос, хороши ли полученные отношения. Заметим пока только, что, как показывают следующие замечания, не любую строку можно добавить в таблицу "Посещать лекции".

Замечание. В таблицу "Посещать лекции" нельзя добавить две одинаковые строки, т.к. таблица изображает отношение 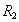, а в отношении (как и в любом множестве) не может быть двух одинаковых элементов. Это пример синтаксического ограничения - такое ограничение задано в определении понятия отношение (одинаковых строк не может быть ни в одной таблице, задающей отношение).

Замечание. В таблицу "Посещать лекции" нельзя добавить кортеж (Иванов, Геометрия, Пушников). Действительно, из таблицы "Читает лекции по…", представляющей отношение 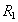, следует, что Пушников не читает предмет "Геометрия". Оказалось, что таблицы связаны друг с другом, и существенным образом! Это пример семантического ограничения - такое ограничение является следствием нашей трактовки данных, хранящихся в отношении (следствием понимания смысла данных).

Дата добавления: 2014-11-29