
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Если же , то в силу (2.1) . 1 страница
|
|
|
|
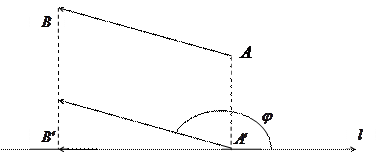
Пусть задана некоторая ось  и
и  . Применяя к каждому из этих векторов формулу (2.2), получим, что
. Применяя к каждому из этих векторов формулу (2.2), получим, что  , т. е. равные векторы имеют равные проекции на одну и ту же ось.
, т. е. равные векторы имеют равные проекции на одну и ту же ось.
Определение. Проекции 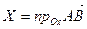 ,
,  ,
, 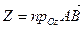 вектора
вектора 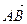 на оси
на оси  ,
,  и
и  прямоугольной системы координат
прямоугольной системы координат  называются координатами вектора
называются координатами вектора 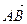 в этой системе координат.
в этой системе координат.
Если для вектора 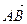
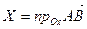 ,
,  ,
, 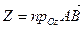 , то символически это записывается в виде
, то символически это записывается в виде
 . (2.3)
. (2.3)
Теорема 2. Для любых двух точек  и
и 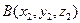 координаты вектора
координаты вектора 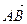 определяются по формулам
определяются по формулам
 ,
,  ,
,  . (2.4)
. (2.4)
Доказательство. Проведем через точки 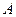 и
и 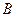 плоскости, перпендикулярные оси
плоскости, перпендикулярные оси 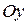 , и обозначим точки пересечения оси
, и обозначим точки пересечения оси  и построенных плоскостей
и построенных плоскостей  и
и 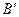 .
.
 |
Точки  и
и 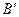 имеют на оси
имеют на оси  координаты
координаты  и
и 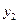 . По определению
. По определению 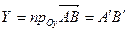 , но
, но  , т. е.
, т. е.  . Аналогично доказываются и остальные соотношения. Теорема доказана.
. Аналогично доказываются и остальные соотношения. Теорема доказана.
Рассмотрим свойства проекций векторов на ось.
Теорема 3. Проекция суммы двух векторов на ось равна сумме их проекций на эту ось, т. е.
 . (2.5)
. (2.5)
Доказательство. Пусть  , тогда, приложив вектор
, тогда, приложив вектор 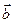 к концу вектора
к концу вектора  , т. е. к точке
, т. е. к точке 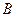 , можем считать, что
, можем считать, что  . Обозначим через
. Обозначим через  ,
, 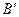 ,
,  проекции точек
проекции точек 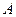 ,
, 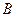 и С на ось
и С на ось  . По определению проекции вектора на ось имеем:
. По определению проекции вектора на ось имеем: 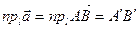 ,
,  ,
, 
 ,
,  (последнее равенство следует из правила сложения величин вещественных чисел).
(последнее равенство следует из правила сложения величин вещественных чисел).
 |
Таким образом,  . Теорема доказана.
. Теорема доказана.
Теорема 4. При умножении вектора  на число
на число  его проекция на ось также умножается на это число, т. е.
его проекция на ось также умножается на это число, т. е.
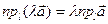 . (2.6)
. (2.6)
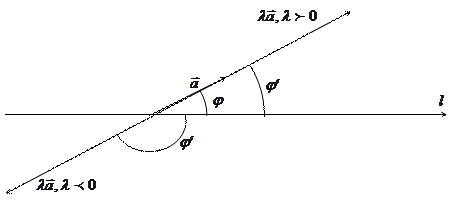
Доказательство. Пусть 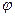 - угол между осью
- угол между осью  и вектором
и вектором  , а
, а  - угол между осью
- угол между осью  и вектором
и вектором 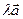 . Если
. Если 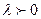 , то векторы
, то векторы  и
и 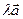 направлены одинаково и
направлены одинаково и  . Если же
. Если же 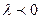 , то векторы
, то векторы  и
и 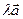 имеют противоположное направление и
имеют противоположное направление и  .
.
 |
Согласно (2.2) при 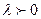 имеем:
имеем:  . Если же
. Если же 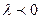 , то
, то  . При
. При  обе части равенства (2.6) обращаются в нуль. Таким образом,
обе части равенства (2.6) обращаются в нуль. Таким образом, 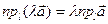 при любых вещественных значениях
при любых вещественных значениях  . Теорема доказана.
. Теорема доказана.
Из этой теоремы вытекает следствие.
Следствие. Если векторы  и
и 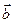 заданы своими координатами, т. е.
заданы своими координатами, т. е. 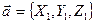 ,
,  , то при любых действительных числах
, то при любых действительных числах  и
и 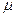 вектор
вектор 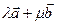 имеет координаты
имеет координаты
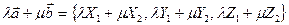 . (2.7)
. (2.7)
Пусть  - углы наклона вектора
- углы наклона вектора 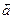 к осям
к осям  ,
,  и
и  соответственно.
соответственно.
Определение. Три числа  ,
,  и
и  называются направляющими косинусами вектора
называются направляющими косинусами вектора  .
.
Из определения координат вектора следует, что если  , то
, то
 ,
,  ,
,  . (2.8)
. (2.8)
Так как  является диагональю прямоугольного параллелепипеда со сторонами, которые отсекают на координатных осях величины
является диагональю прямоугольного параллелепипеда со сторонами, которые отсекают на координатных осях величины  ,
,  и
и  , то
, то
 . (2.9)
. (2.9)
Из формул (2.8) и (2.9) находятся выражения для направляющих косинусов вектора  через его координаты:
через его координаты:
 ,
,  ,
, 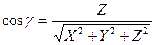 . (2.10)
. (2.10)
Возводя полученные равенства в квадрат и складывая, получим, что  , т. е. сумма квадратов направляющих косинусов любого вектора равна единице.
, т. е. сумма квадратов направляющих косинусов любого вектора равна единице.
Так как вектор  однозначно определяется заданием трех его координат, из полученных формул (2.8) следует, что вектор
однозначно определяется заданием трех его координат, из полученных формул (2.8) следует, что вектор  однозначно определяется заданием его длины и трех направляющих косинусов.
однозначно определяется заданием его длины и трех направляющих косинусов.
П р и м е р 22. Даны два вектора  и
и  . Найти проекции на координатные оси векторов
. Найти проекции на координатные оси векторов  и
и 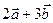 .
.
Решение. Проекциями вектора на координатные оси являются его координаты. По формуле (2.7) получим:  ,
,  .
.
2.5. Скалярное произведение векторов
Определение. Скалярным произведением двух ненулевых векторов  и
и 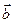 называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними, т. е.
называется число (скаляр), равное произведению длин этих векторов на косинус угла между ними, т. е.
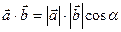 , (2.16)
, (2.16)
где  - угол между векторами
- угол между векторами  и
и 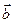 .
.
Если хотя бы один из векторов  или
или 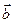 - нулевой, то угол между векторами не определен, и скалярное произведение полагается равным нулю.
- нулевой, то угол между векторами не определен, и скалярное произведение полагается равным нулю.
Проекцию вектора 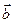 на ось, определяемую вектором
на ось, определяемую вектором  , обозначим
, обозначим  . По определению проекции вектора на ось имеем:
. По определению проекции вектора на ось имеем:  . Тогда скалярное произведение двух ненулевых векторов
. Тогда скалярное произведение двух ненулевых векторов  и
и 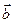 определяется формулой
определяется формулой
 . (2.17)
. (2.17)
Учитывая, что в определении скалярного произведения векторы  и
и 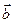 взаимозаменяемые, его можно представить в виде
взаимозаменяемые, его можно представить в виде
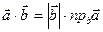 . (2.18)
. (2.18)
Соотношения (2.17) и (2.18) позволяют сформулировать другое определение скалярного произведения.
Определение. Скалярным произведением двух ненулевых векторов  и
и 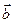 называется число (скаляр), равное произведению длины одного из этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов.
называется число (скаляр), равное произведению длины одного из этих векторов на проекцию другого вектора на ось, определяемую первым из указанных векторов.
Физический смысл скалярного произведения заключается в следующем: если точка приложения силы, задаваемой постоянным вектором 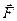 , перемещается вдоль вектора
, перемещается вдоль вектора  , то работа этой силы определяется равенством
, то работа этой силы определяется равенством  , где
, где  - угол между векторами
- угол между векторами  и
и 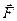 , т. е. работа равна скалярному произведению векторов
, т. е. работа равна скалярному произведению векторов  и
и 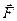 .
.
Теорема 8. Необходимым и достаточным условием ортогональности (перпендикулярности) двух векторов является равенство нулю их скалярного произведения.
Доказательство. Необходимость. Пусть векторы  и
и 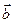 ортогональны,
ортогональны,  - угол между ними, тогда
- угол между ними, тогда  , и в силу формулы (2.16)
, и в силу формулы (2.16)  .
.
Достаточность. Пусть  . Докажем, что векторы
. Докажем, что векторы  и
и 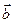 ортогональны. Если хотя бы один из векторов равен нулевому вектору, то он имеет неопределенное направление, и можно считать, что векторы ортогональны. Если оба вектора
ортогональны. Если хотя бы один из векторов равен нулевому вектору, то он имеет неопределенное направление, и можно считать, что векторы ортогональны. Если оба вектора  и
и 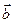 ненулевые, то
ненулевые, то 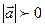 ,
, 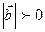 , поэтому из (2.16) следует, что
, поэтому из (2.16) следует, что  , т, е. векторы
, т, е. векторы  и
и 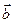 ортогональны. Теорема доказана.
ортогональны. Теорема доказана.
Если два вектора привести к общему началу, то в качестве угла  между этими векторами можно взять любой из углов
между этими векторами можно взять любой из углов 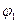 или
или  .
.
 |
Действительно, сумма углов 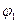 и
и  равна
равна 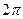 , поэтому
, поэтому  . В определение скалярного произведения входит сомножителем только косинус угла между векторами. Из двух углов
. В определение скалярного произведения входит сомножителем только косинус угла между векторами. Из двух углов 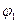 и
и  между векторами один всегда не более
между векторами один всегда не более 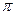 . За угол
. За угол  между векторами принимается наименьший из углов
между векторами принимается наименьший из углов 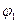 и
и  , т. е.
, т. е. 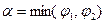 .
.
Если скалярное произведение двух ненулевых неколлинеарных векторов  и
и 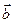 положительно (отрицательно), то эти два вектора составляют острый (тупой) угол.
положительно (отрицательно), то эти два вектора составляют острый (тупой) угол.
Свойства скалярного произведения:
1.  .
.
Доказательство. Это свойство непосредственно вытекает из определения скалярного произведения:  . Свойство доказано.
. Свойство доказано.
2.  .
.
Доказательство. Для доказательства этого свойства воспользуемся формулой (2.18) для определения скалярного произведения и свойствами проекций векторов на ось: 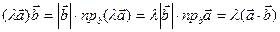 . Свойство доказано.
. Свойство доказано.
3.  .
.
Доказательство. Воспользуемся формулой (2.18) для определения скалярного произведения и свойствами проекций векторов на ось. Получим:  . Свойство доказано.
. Свойство доказано.
4.  , если
, если  , и
, и  , если
, если  .
.
Доказательство. Из определения скалярного произведения с использованием соотношения (2.16) следует, что 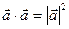 . Если
. Если  , то
, то  и
и  . Если же
. Если же  , то
, то 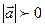 , поэтому
, поэтому  . Свойство доказано.
. Свойство доказано.
Эти свойства позволяют при скалярном перемножении векторных многочленов выполнять действия почленно, не учитывая порядок векторных сомножителей и сочетая числовые множители.
Из определения и свойств скалярного произведения векторов следует, что для базисных векторов 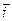 ,
, 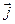 ,
, 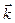 выполняются соотношения
выполняются соотношения
a) 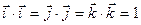 ; (2.19)
; (2.19)
b)  . (2.20)
. (2.20)
Теорема 9. Если векторы  и
и 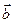 заданы своими координатами, т. е.
заданы своими координатами, т. е. 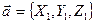 ,
,  , то скалярное произведение векторов
, то скалярное произведение векторов  и
и 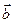 вычисляется по формуле
вычисляется по формуле
 . (2.21)
. (2.21)
Доказательство. Разложим векторы  и
и 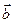 по базису
по базису 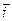 ,
, 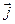 ,
, 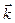 , получим
, получим 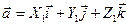 ,
, 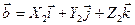 . Тогда по свойствам скалярного произведения векторов, используя формулы (2.19), (2.20), имеем
. Тогда по свойствам скалярного произведения векторов, используя формулы (2.19), (2.20), имеем 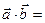
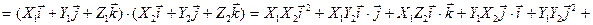
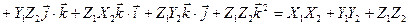 . Теорема доказана.
. Теорема доказана.
Следствие. Угол  между ненулевыми векторами
между ненулевыми векторами 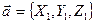 и
и  определяется по формуле
определяется по формуле
 . (2.22)
. (2.22)
Доказательство. По определению скалярного произведения двух ненулевых векторов 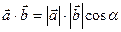 , поэтому
, поэтому  . Воспользовавшись формулами (2.21) и (2.9) для скалярного произведения и длин векторов, заданных своими координатами, получим формулу (2.22).
. Воспользовавшись формулами (2.21) и (2.9) для скалярного произведения и длин векторов, заданных своими координатами, получим формулу (2.22).
Замечание. Если один из векторов  или
или 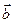 является нулевым, то угол между векторами определяется неоднозначно и может быть выбран произвольным.
является нулевым, то угол между векторами определяется неоднозначно и может быть выбран произвольным.
П р и м е р 24. Дано, что  ,
,  . Определить, при каком значении
. Определить, при каком значении  векторы
векторы  и
и 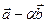 будут взаимно перпендикулярны.
будут взаимно перпендикулярны.
Решение. Условием перпендикулярности векторов является равенство нулю их скалярного произведения, т. е. 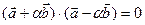 . По свойствам скалярного произведения
. По свойствам скалярного произведения 
 . Таким образом,
. Таким образом,  , или
, или  .
.
П р и м е р 25. Векторы  и
и 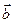 образуют угол
образуют угол  . Зная, что
. Зная, что  ,
,  , вычислить угол
, вычислить угол  между векторами
между векторами  и
и  .
.
Решение. Для нахождения косинуса угла  между векторами
между векторами  и
и  воспользуемся соотношением (2.22). По формуле (2.21):
воспользуемся соотношением (2.22). По формуле (2.21):  . Найдем длины векторов
. Найдем длины векторов  и
и  , используя свойства скалярного произведения:
, используя свойства скалярного произведения: 
 . Аналогично находим, что
. Аналогично находим, что  . Тогда
. Тогда  и
и 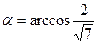 .
.
2.6. Векторное произведение векторов
Определение. Тройка векторов называется упорядоченной, если указано, какой из векторов считается первым, какой - вторым, а какой - третьим.
Например,  - упорядоченная тройка векторов, в которой первым вектором является вектор
- упорядоченная тройка векторов, в которой первым вектором является вектор 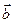 , вторым - вектор
, вторым - вектор  , третьим - вектор
, третьим - вектор  .
.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 852; Нарушение авторских прав?; Мы поможем в написании вашей работы!