Механические свойства льда

Механические свойства ледяного покрова изучают в лабораторных условиях. С помощью гидравлического пресса испытывают образцы льда на сжатие, изгиб и растяжение. Во время испытаний к образцу прикладывают равномерно возрастающие статические нагрузки. По достижению некоторого критического значения происходит разрушение образца. По полученным зависимостям деформации от напряжения можно судить о прочностных характеристиках льда. Подробно процесс исследования механических свойств льда описан в [2].

Изучение механических свойств льда необходимо для защиты гидротехнических сооружений от разрушающего действия на них ледяного покрова.

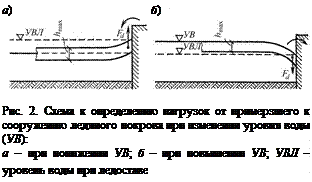
Рассмотрим определение вертикальной силы (F_d) от примерзшего к сооружению ледяного покрова при изменении уровня воды (рис. 2):

,

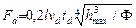где l – длина участка сооружения на уровне действия льда, м; v_d – скорость повышения или понижения уровня воды, м/ч; t_d – время, в течение которого происходит деформация ледяного покрова при понижении или повышении уровня воды, ч; h _max – максимальная высота ледяного покрова; F – безразмерная функция времени, определяемая по формуле

.

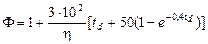Значение вертикальной силы можно получить в зависимости от времени, которое входит и в первую, и во вторую формулы.

Для реализации этой зависимости и для моделирования испытаний над ледяными образцами в пакете MatLab следует знать управляющие структуры и методы их реализации.

Для написания программ на языке MatLab служат m -файлы. Подготовленный и записанный на диск m -файл становится частью системы, и его можно вызывать как из командной строки, так и из другого m -файла. Есть два типа m -файлов: файлы-сценарии и файлы-функции.

Файл-сценарий,именуемый также Script -файлом, является просто записью серии команд без входных и выходных параметров. Он имеет следующую структуру:

%Основной комментарий

%Дополнительный комментарий

Тело файла с любыми выражениями

Важны следующие свойства файлов-сценариев:

– они не имеют входных и выходных аргументов;

– работают с данными из рабочей области;

– в процессе выполнения не компилируются;

– представляют собой зафиксированную в виде файла последовательность операций, полностью аналогичную той, что используется в сессии.

Основным комментарием является первая строка текстовых комментариев, а дополнительным – последующие строки. Основной комментарий выводится при выполнении команд lookfor и help имя_каталога. Полный комментарий выводится при выполнении команды help имя_файла.

М -файл-функция является типичным объектом языка программирования системы MatLab. Структура этого структурированного модуля с одним выходным параметром выглядит следующим образом:

function var = f_name(Список_параметров)

%Основной комментарий

%Дополнительный комментарий

Тело файла с любыми выражениями

vаr = выражение

М -файл-функция имеет следующие свойства:

– он начинается с объявления function, после которого указывается имя переменной var – выходного параметра, имя самой функции и список ее входных параметров;

– функция возвращает свое значение и может использоваться в виде name (Список_параметров) в математических выражениях;

– все переменные, имеющиеся в теле файла-функции, являются локальными, т. е. действуют только в пределах тела функции;

– файл-функция является самостоятельным программным модулем, который общается с другими модулями через свои входные и выходные параметры;

– правила вывода комментариев те же, что у файлов-сценариев;

– файл-функция служит средством расширения системы MatLab;

– при обнаружении файла-функции он компилируется и затем исполняется, а созданные машинные коды хранятся в рабочей области системы MatLab.

Последняя конструкция vаr = выражение вводится, если требуется, чтобы функция возвращала результат вычислений. Если выходных параметров больше, то они указываются в квадратных скобках после слова function.

Любая серьезная программа имеет нелинейную структуру. Для создания таких программ необходимы специальные управляющие структуры.

1. Диалоговый ввод и вывод:

input ('Комментарий', 's') или var = input ('Введите var');

disp ('Комментарий') или disp (var).

В первых случаях функции input и disp используются для ввода/вывода произвольного строкового выражения, а во вторых – для ввода/вывода значения var.

2. Условный оператор:

if Условие

Инструкции_1

elself Условие

Инструкции_2

else

Инструкции_3

end

Пока Условие возвращает логическое значение 1 (т. е. «истина»), выполняются Инструкции, составляющие тело структуры if... end. Инструкции в списке разделяются оператором, (запятая) или; (точка с запятой). В Условии должны быть использованы следующие операторы отношения: ==, <, >, <=, >= или ~=. Все эти операторы представляют собой пары символов без пробелов между ними.

3. Циклы типа for... end обычно используются для организации вычислений с заданным числом повторяющихся циклов. Конструкция такого цикла имеет следующий вид:

for vаr = Выражение, Инструкция, …, Инструкция end

Выражение чаще всего записывается в виде s: d: e, где s – начальное значение переменной цикла var, d – приращение этой переменной и е – конечное значение управляющей переменной, при достижении которого цикл завершается. Возможна и запись в виде s: e (в этом случае d = l). В примере иллюстрируется формирование двумерной матрицы:

for i=1:3

for j=l:3

А(i, j) = i+j;

end

end

Следует отметить, что формирование матриц с помощью оператора: (двоеточие) обычно занимает намного меньше времени, чем с помощью цикла.

4. Цикл типа while выполняется до тех пор, пока выполняется Условие:

while Условие

Инструкции

end

Рассмотрим функцию, которая необходима для изображения зависимостей: функция testvarin выводит на экран линии соединяющие последовательность точек с координатами х и у. Точки задаются векторами из двух элементов. Функция testvarin допускает в качестве входного аргумента любое количество таких векторов.

function testvarin (varargin)

for i = 1:length(varargin)

x(i) = varargin{i} (1);

y(i) = varargin{i} (2);

end

xmin = min(0, min(x));

ymin = min(0, min(y));

axis([xmin fix(max(x))+3 ymin fix(max(y))+3])

plot(x,y)

Список varargin хранит входные переменные в массиве ячеек. Так, например, координаты х и у точки с индексом i – это соответственно первый и второй элементы i -й ячейки массива varargin.

Дата добавления: 2014-11-29