Свойства воды. Из сказок известно, что существует живая вода – это вода, дающая молодость, здоровье, жизнь и мертвая вода – погружающая человека в сон

Из сказок известно, что существует живая вода – это вода, дающая молодость, здоровье, жизнь и мертвая вода – погружающая человека в сон, подобный смерти.

Подобие живой и мертвой воды существует в природе: живая, животворная – это талая вода, образовавшаяся от растаявшего снега или льда; мертвая, не утоляющая жажду и губящая все живое, – это тяжелая вода.

Более ста лет после того, как Лавуазье, Пристли, Гемфри Дэви установили, что вода состоит из двух объемов водорода и одного объема кислорода, физикам и химикам не удавалось узнать ничего нового о воде. Но вот в 1932 г. американцы Г. Юри и Э. Осборн обнаружили, что даже в самой чистой воде, которую только можно получить в лабораторных условиях, содержится незначительное количество какого-то вещества, выражающегося, по-видимому, той же химической формулой Н₂О, но обладающего молекулярным весом 20 вместо веса 18, присущего обычной воде. Юри назвал это вещество тяжелой водой. Больший вес тяжелой воды объясняется тем, что ее молекулы состоят из атомов водорода с удвоенным атомным весом по сравнению с атомами обычного водорода.

Двойной вес этих атомов в свою очередь обусловливается тем, что их ядра содержат, кроме единственного протона, составляющего ядро обычного водорода, еще один нейтрон. Тяжелый изотоп водорода получил название дейтерия (D или Н²), а обычный водород стали называть протием. Тяжелая вода, окись дейтерия, выражается формулой D₂O.

Вскоре был открыт третий, сверхтяжелый изотоп водорода с одним протоном и двумя нейтронами в ядре, который был назван тритием (обозначается Т или Н³).[1] В соединении с кислородом тритий образует сверхтяжелую воду Т₂О с молекулярным весом 22.

Кроме того, были найдены три изотопа кислорода с атомными весами 16 (обыкновенный кислород), 17 и 18. Все вновь открытые изотопы водорода и кислорода в общей сложности составляют лишь ничтожную часть воды, поэтому в природных водах содержится в среднем около 0,016% тяжелой воды, т. е. на один атом дейтерия приходится 6600 атомов протия. Таким образом, почти вся вода в природе является тем, чем ее давно считали, а именно – соединением самых обычных изотопов водорода (протия) и кислорода, т. е. H₂O.

Тяжелая вода внешне похожа на обычную воду, но по многим физическим свойствам она отличается от нее. Точка кипения тяжелой воды 101,4°С, точка замерзания +3,8°С. Тяжелая вода на 11 % тяжелее обычной. Самую большую плотность тяжелая вода имеет при 11°С. Ее удельный вес при 25 °С равен 1,1. Она хуже (на 5–15%) растворяет различные соли. В тяжелой воде скорость протекания некоторых химических реакций иная, чем в обычной воде, например, разложение электрическим током на водород и кислород происходит в пять раз медленнее. Обычная вода испаряется легче, поэтому неиспарившийся остаток ее обогащается тяжелой водой.

И в физиологическом отношении тяжелая вода воздействует на живое вещество иначе: в отличие от Н₂О, обладающей живительной силой, тяжелая вода совершенно инертна. Семена растений, если их поливать тяжелой водой, не прорастают; головастики, микробы, черви, рыбы в такой воде не могут существовать; если животных поить одной тяжелой водой, они погибают от жажды.

Тяжелая вода – это мертвая вода. Символично, что один из составляющих ее элементов, а именно дейтерий, используется как ядерное горючее для водородной бомбы. Кроме того, тяжелая вода применяется в реакторах атомных электростанций для замедления нейтронов, которое необходимо для поддержания цепной реакции деления урана.

Было высказано предположение, что тяжелая вода, вернее, тяжелый водород, должна постепенно накапливаться в нашем организме и действительно становиться своего рода тормозом для жизненных функций, замедляющим обмен веществ. А ведь жизнь – это обмен веществ.

Логический вывод из этих рассуждений – «Не пейте тяжелой, мертвой воды. Пейте живую воду, освобожденную от дейтерия!»

Но избавиться от него пока практически невозможно. Впрочем, вскоре было обнаружено, что «живая вода» – талая вода. Ее чудесные целебные свойства связывают не с отсутствием в ней дейтерия (его столько же, сколько и в любой другой воде), а с тем, что в течение некоторого времени после образования талая вода частично сохраняет еще структуру льда, более «рыхлую», чем структура жидкой воды, в которой молекулы «упакованы» плотнее.

Ледяные структуры, легко проникая в ткани человека и животных, оказывают омолаживающее и оздоравливающее действие на организм. В литературе имеются указания, что талая вода увеличивает прирост веса молодняка, яйценоскость кур, молочность коров. Прокипяченная талая вода теряет свои чудесные свойства.

Может быть, березовый сок, собираемый ранней весной, который считается в народной медицине тоже полезным для здоровья, оттого и полезен, что представляет собой талую воду, прошедшую через живые клетки и обогатившуюся витаминами.

Другой вид живой воды, так называемая серебряная вода, был известен в глубокой древности. Это вода, бывшая в течение некоторого времени в соприкосновении с серебром или содержащая электролитический раствор серебра.

Еще 2500 лет назад персидский царь Кир в походах в Индию и Малую Азию пользовался питьевой водой, хранившейся в серебряных сосудах, чтобы предохранить ее от порчи. В 1893 г. швейцарский ботаник К. Негели впервые сообщил в печати об открытом им свойстве серебра при контакте с водой убивать находящиеся в ней микроорганизмы.

В нашей стране и за рубежом были выполнены исследования бактерицидных и лечебных свойств серебряной воды, разработаны эффективные способы ее получения и применения, создана соответствующая аппаратура. Приборами для получения серебряной воды оборудовано более 40 крупных морских судов. Космонавт В. Быковский пользовался в полете серебряной водой.

Имеется еще один вид воды, отличающийся по физическим свойствам от обычной воды, – это омагниченная вода. Такую воду получают с помощью магнитов, вмонтированных в трубопровод, по которому течет вода. Вода, проходя через невидимые силовые линии магнитного поля, изменяет некоторые свои физико-химические свойства, скорость химических реакций в ней увеличивается, ускоряется кристаллизация растворенных веществ, увеличивается слипание твердых частиц примесей и выпадение их в осадок с образованием крупных хлопьев (коагуляция). Омагничивание успешно применяется на водопроводных станциях при большой мутности забираемой воды, оно позволяет также быстро осаждать загрязненные промышленные стоки. Наиболее эффективной областью применения воды магнитной обработки оказалась борьба с накипью паровых котлов: использование омагниченной воды в котлах практически прекращает оседание на их стенках накипеобразующих солей.

Причины изменений свойств воды под воздействием магнитного поля пока не вполне ясны.

Важным свойством жидкости (воды) как материала является вязкость. Вязкость – свойство жидкости, обусловливающее появление касательных напряжений между слоями движущейся жидкости при их относительном перемещении. Количественной мерой вязкости являются величины динамической m (Н×с/м²) и кинематической u (стокс (Ст), 1 Ст = 10^–4 м²/с) вязкостей. Они связаны соотношением

,

где r – плотность жидкости.

Динамический коэффициент вязкости воды в сильной степени зависит от температуры и мало зависит от давления. При расчете динамического коэффициента вязкости применяют эмпирическую формулу Пуазейля:

m = 0,000183/(1 + 0,0337 t + 0,000221 t ²),

где t – температура воды.

Динамический коэффициент вязкости соленой воды незначительно отличается от коэффициента вязкости пресной воды. Например, при t = 20°C и S = 25°/₀₀ он равен 1,052 ×10^–3 Па×с, а для пресной воды – 1,003 ×10^–3 Па×с, т. е. больше примерно на 5%.

С ростом температуры жидкости значения m и u уменьшаются (для газов возрастают), а с увеличением давления – несколько увеличиваются. Значения m для воды, ртути, керосина и бензина приведены в табл. 2.

Таблица 2.

Значения динамической вязкости для некоторых жидкостей (m×10³, Н×с/м²)

Температура, °С	Дистиллированная вода	Ртуть	Керосин	Бензин
	1,7525	1,687	2,15	0,735
	1,2992	–	1,73	0,643
	1,0015	1,556	1,49	0,529
	0,7970	–	–	–
	0,6513	1,457	1,08	0,411
	0,5440	–	–	–
	0,4630	1,372	0,832	0,328
	0,4005	–	–	–
	0,3510	1,301	0,664	0,269
	0,3113	–	–	–
	0,2790	1,241	0,545	0,225
	0,1338	1,039	0,262	0,111

Отметим, что жидкость, не обладающая вязкостью, поверхностным натяжением и не изменяющая объема при изменении температуры и давления, называется идеальной. К идеальной жидкости близок по свойствам жидкий гелий.

Рассмотрим зависимость кинематической вязкости и удельной потери h _п энергии (потери напора) при перемещении единицы массы вязкой жидкости. Вспомним уравнение Бернулли для больших потоков вязкой жидкости с неравномерным полем скоростей по нормальным и медленно изменяющимся вдоль потока сечениям:

,

где и 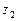– расстояние от плоскости сравнения до центров тяжести нормальных сечений I и II; p ₁ и p ₂ – давления в этих сечениях на уровне центров тяжести; n_1ср и n_2ср – средние скорости в сечениях I и II; a₁ и a₂ – безразмерные коэффициенты кинетической энергии (коэффициенты Кориолиса); g – ускорение свободного падения; g – удельный объем жидкости.

Из уравнения Бернулли выводится зависимость кинематической вязкости и потери напора в трубах при ламинарном режиме потока.

Кроме труб ламинарный режим может существовать при протекании жидкости в щелях малого сечения, в капиллярах, в смазочном слое гидродинамических подшипников.

При ламинарном режиме поток на входе в трубу круглого сечения диаметром d (рис. 1) формируется так, что там создается равномерное поле скоростей по всему нормальному сечению потока (за исключением бесконечно тонкого слоя у стенок трубы, где имеет место прилипание жидкого слоя, т. е. его скорость v = 0). В последующих сечениях центральный участок с равномерным полем скоростей (ядро потока) уменьшается и вытягивается из-за тормозящего действия слоя, прилипшего к стенкам трубы. При этом возрастает толщина слоя d, на который распространяется торможение, обусловленное стенками трубы. Этот слой называют пограничным. На расстоянии l _нач от входа в трубу значение d доходит до d = d /2, т. е. ядро сечения полностью ликвидируется; с этого момента начинается равномерное движение жидкости в трубе.

При ламинарном режиме длина начального участка

l _нач» 0,029 Re d,

где Re – число Рейнольдса.

Поле скоростей v в любом сечении за начальным участком имеет параболическую форму с максимальной скоростью по оси трубы

v _max = 2 v _ср.

На радиусе r трубы

,

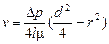где D р – перепад давления на участке горизонтальной трубы длиной l; m – динамическая вязкость жидкости.

С учетом выше приведенного уравнения для равномерного движения потока в трубе круглого сечения при ламинарном режиме коэффициент кинетической энергии a = 2. В этом же случае потери напора на гидравлическое трение h _п = h_l на участке трубы диаметром d и длиной l, входящие в уравнение Бернулли, определяют по формуле

,

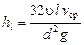u – кинематическая вязкость жидкости; g – ускорение свободного падения.

Заменяя v _cp на Q/(p* d ²/4), получим явную зависимость h_l от кинематической вязкости при ламинарном режиме:

.

Для того чтобы графически реализовать эту зависимость в пакете MatLab необходимо знать следующие пункты.

1. Основным видом данных, которые используются в пакете MatLab (сокр. от англ. Matrix Laboratory – дословно «Матричная лаборатория»), являются матрицы. Даже общепринятые скалярные переменные рассматриваются как матрицы размерности 1´1.

2. Числовые данные, с которыми оперирует MatLab, в памяти компьютера представлены в формате double. Это означает, что каждое вещественное число занимает 8 байт в оперативной памяти и принимает по модулю значения из диапазона [10^-308, 10⁺³⁰⁸]. Количество значащих десятичных цифр при этом достигает 16–17. Изменить формат данных можно в подпункте Свойства (Preference) пункта Файл (File) окна управления.

3. Необходимо обратить внимание на то, что следует: 1) при задании массива значениями заключать их в квадратные скобки; 2) элементы в строке массива разделять пробелами или запятыми; 3) при указании списка индексов использовать круглые скобки и разделительные запятые (указание индекса символом двоеточия соответствует заданию всех значений по соответствующему индексу).

4. При работе с массивами можно пользоваться списками i: k и i: j: k. В первом варианте понимается, что «от i до k с шагом 1» и во втором – то же с шагом j.

5. Приходится различать поэлементные операции с массивами и операции над матрицами по правилам линейной алгебры (для массивов перед знаком операции ставят точку).

6. Для того чтобы построить график функции y = f (x), необходимо сформировать два вектора одинаковой размерности – вектор значений аргументов (х) и вектор соответствующих значений функции (у), и обратиться к процедуре plot.

Пример: построение графика функции y = sin (x) * e^{– x}

>> x = 0:0.1:6.28

% изменение аргумента x от 0 до 6,28 с шагом 0,1

>> y = sin(x).*exp(-x)

>> plot (x, y, ‘:g’)

Дополнительный параметр в процедуре plot – символ, ассоциированный с одним из 8 предусмотренных цветов: у – желтый (от yellow); g – зеленый (от green); m – малиновый (от magenta); b – синий (от blue); с – циановый (от cyan); w – белый (от white); r – красный (от red); k – черный (от black).

Вид графика можно изменить, задав стиль линии и форму маркера, которым метятся табличные точки. Стиль линии предусматривает выбор одной из четырех возможностей – сплошная линия (по умолчанию, управляющий символ – тире), пунктирная линия (управляющий символ – двоеточие), штрих-пунктирная линия (управляющие символы – тире и точка), штриховая линия (управляющие символы – два тире). Управляющие символы, определяющие стиль линии, задаются в строке третьего параметра вместе с цветом. Порядок следования символов – любой.

Дополнительные украшения графика заключаются в возможности снабдить его заголовком (процедура title), подписать оси (процедуры xlabel, ylabel), нанести координатную сетку (процедура grid on) и разместить легенду (процедура legend).

Для совмещение двух графиков в одном окне MatLab предлагает процедуру plotyy, которая производит двойную оцифровку осей. Для первой функции цифруются ось х внизу, ось у слева, а для второй функции ось х размечается вверху, ось у – справа. Цвет оцифровки при этом совпадает с цветом кривых.

Может оказаться, что в одном графическом окне необходимо отобразить большее число графиков. Тогда можно прибегнуть к функции subplot, которая позволяет разделить область рисования на несколько прямоугольных областей равного размера, расположенных подобно элементам матрицы:

>> subplot (row, col, cur);

Первые два аргумента задают количество рядов (row) и колонок (col). Третий параметр (cur) объявляет порядковый номер подобласти, в котором очередная функция plot будет строить свой график.

Дата добавления: 2014-11-29