Маятниковый маршрут с обратным порожним пробегом

Матрица для определения рационального порядка объезда пунктов по маршруту № 2

Номер строки	А	5,6	5,2	8,0	3,2
	5,6	Ж	5,0	5,8	7,0
	5,2	5,0	Д	2,8	2,0
	8,0	5,8	2,8	И	4,8
	3,2	7,0	2,0	4,8	Г
å		23,4		21,4

Получается маршрут вида: А à Ж à И à А.

Включается пункт Г:

DАЖ = САГ + СГЖ – САЖ = 3,2 + 7,0 – 5,6 = 4,6 км;

DЖИ = СЖГ + СГИ – СЖИ = 7,0 + 4,8 – 5,8 = 6,0 км;

DИА = СИГ + СГА – СИА = 4,8 + 3,2 – 8,0 = 0 км.

Получается маршрут вида: А à Ж à И à Г à А.

Включается пункт Д:

DАЖ = САД + СДЖ – САЖ = 5,2 + 5,0 – 5,6 = 4,6 км;

DЖИ = СЖД + СДИ – СЖИ = 5,0 + 2,8 – 5,8 = 2,0 км;

DИГ = СИД + СДГ – СИГ = 2,8 + 2,0 – 4,8 = 0 км.

Окончательный порядок движения по маршруту 2: А à Ж à И à Д à Г à А.

Общий пробег по маршрутам составляет:

маршрут 1: А – К – З – Е – В – Б – А = 10,6 + 2,0 + 2,4 + 3,6 + 2,2 + 7,0 = 27,8 км;

маршрут 2: А – Ж – И – Д – Г – А = 5,6 + 5,8 + 2,8 + 2,0 + 3,2 = 19,4 км.

Таким образом, общий километраж по этим маршрутам составит: 27,8 + 19,4 = 47,2 км.

Задача составления рациональных маятниковых маршрутов, обеспечивающих минимальный порожний пробег транспортных средств, сводится к следующей задаче линейного программирования:

(4.1)

минимизировать линейную формулу:

при условиях:

(4.2)

пункты назначения пронумерованы в порядке возрастания разностей :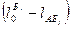

(4.3)

Тогда оптимальное решение таково:

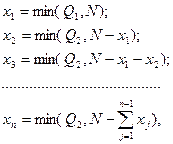(4.4)

где L – порожний пробег, км;

– расстояние от пункта назначения до АТП (второй нулевой пробег), км;

– расстояние от А до Б – груженый пробег, км;

N – число автомобилей, работающих на всех маршрутах;

x_j – количество автомобилей, работающих с последним пунктом разгрузки;

j – номер (индекс) потребителя (j = 1, 2, 3…, n);

А – поставщик (распределительный центр);

Б_j – пункты потребления;

Q_j – объем перевозок (в ездках автомобиля).

Решая эту задачу, нужно знать, что наилучшее решение получается при такой системе маршрутов, когда максимальное число автомобилей заканчивает работу в пунктах назначения с минимальными разностями т.е. второго нулевого и груженого пробега.

Для решения задачи необходимо исходные данные записать в специальную матрицу (табл. 4.1), чтобы с ее помощью произвести все необходимые вычисления по составлению маршрутов.

Таблица 4.1

Дата добавления: 2014-11-29