
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Построение графика PX
|
|
|
|
Протокол № 2 2 серия
| Порядковый номер пробы | Вид пробы | Ответ испытуемого | Исход пробы |
| S | нет | N/S – пропуск стимула | |
| n | Да | Y/n – ложная тревога | |
| S | да | Y/S – правильное обнаружение | |
| n | нет | N/n – правильное отрицание | |
| S | нет | N/S – пропуск стимула | |
| ... | ... | ... | ... |
| S | да | Y/S – правильное обнаружение | |
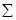 (S) = 150 (S) = 150
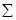 (n) = 50 (n) = 50
| 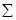 (Y/S) = (Y/S) = 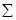 обн = 119 обн = 119
 (Y/n) = (Y/n) = 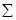 лт = 24 лт = 24
|
Используя алгоритм, уже применявшийся для расчетов Pобн и Pлт в первой серии, во второй серии получаем:
Pобн = 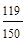 = 0,79;
= 0,79;
Pлт = 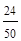 = 0,48.
= 0,48.
Таким образом, изменив значение априорных вероятностей появления стимула в пробе q(S) и его отсутствия q(n), получаем увеличение и Pобн, и одновременно Pлт, что совершенно закономерно.
Графически построение PX возможно двумя способами:
а) в линейных координатах (по оси x - Pлт, по оси y - Pобн);
b) в Z-координатах (так называемых «двойных нормальных» координатах: по оси x - Z лт, по оси y - Z обн).
Построение графика РХ в общем виде в обычной системе координат нами уже производилось в 2.2.3 (см. рис.8). При построении РХ этим способом по экспериментальным данным достаточно нанести на поле графика две точки с координатами, полученными в 1 и 2 сериях (рис.13).
Для каждой экспериментальной точки определяются доверительные интервалы (при выбранной доверительной вероятности β) по осям Pобн и Pлт – на рисунке они представлены в виде горизонтальных и вертикальных отрезков, проходящих через экспериментальные точки. На практике построение такой PX применяется редко, так как не дает простого способа графического расчета d¢.
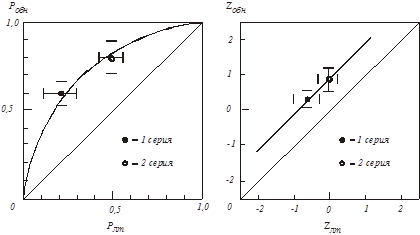
Рис.13. Рабочие характеристики наблюдателя в линейных (слева) и двойных нормальных (справа) координатах (β≤0,95)
Гораздо чаще встречается построение PX в Z-координатах, которые также называются двойными нормальными координатами, поскольку построены исходя из предположения, что исходные величины подвергаются Z-преобразованию Фишера, опирающемуся на нормальный (гауссовский) закон распределения плотности вероятности. В используемом нами подходе предполагается, что распределения сенсорных эффектов f(s) и f(n) подчиняются именно нормальному закону распределения.
Для того, чтобы построить PX в Z-координатах, надо перевести значения Pобн и Pлт в Z-единицы. Сделать это можно, используя специальные таблицы Z-преобразования, где даны рассчитанные значения интеграла нормального распределения, и которые приводятся в любом руководстве по теории вероятности и математической статистике.
Для нашего примера имеем:
I серия: 
II серия: 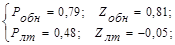
Теперь, используя Z-координаты, строим новый вариант PX (см. рис.13, справа). Функция PX в этих координатах представляет собой прямую, проходящую через экспериментальные точки и параллельную главной диагонали. Понятно, что построить такую линейную функцию гораздо легче, чем сложную кривую, какой является РХ в обычных координатах.
3) Расчет показателя чувствительности d¢.
Полученные выше значения Z обн и Z лт характеризуют, соответственно, расстояние по оси сенсорных эффектов s от MS до критической точки s0 (Z обн ) и от Mn до s0 (Z лт); выраженное в единицах  (при условии
(при условии  =
=  =
=  ):
):
Z обн =  ; (20 a)
; (20 a)
Z лт =  . (20 b)
. (20 b)
Поскольку, по определению (18), имеем:
d¢ =  , (21)
, (21)
то, преобразуя это выражение прибавлением и вычитанием в числителе s0, получаем:
d¢ =  –
– 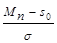 . (22)
. (22)
Последнее выражение можно переписать в более простом виде, используя записанные выше обозначения Z обн и Z лт (20a,b):
d¢ = Z обн – Z лт (23)
Эта формула является основной для расчета количественных значений показателя чувствительности d¢ и используется в подавляющем большинстве работ из-за простоты и легкости ее применения.
Используя формулу (24) для разбиравшихся в этом разделе примеров, получим следующие значения d¢:
I серия: d¢ 1 = 0,28 - (-0,64) = 0,26 + 0,64 = 0,90;
II серия: d¢ 2 = 0,81 - (-0,05) = 0,81 + 0,05 = 0,86.
То есть полученные в первой и второй сериях значения d¢ практически совпали, хотя это и не всегда получается в реальности.
Графически величина d¢ в Z-координатах представляет собой не что иное, как кратчайшее расстояние от любой точки прямой РХ до главной диагонали.
|
|
|
|
|
Дата добавления: 2014-11-29; Просмотров: 519; Нарушение авторских прав?; Мы поможем в написании вашей работы!