Способ расчета Pобн и Pлт в методе оценки

⇐ Предыдущая 14 15 16 17 181920 21 Следующая ⇒

Значения P(k/s) и P(k/n) для всех оценочных категорий

Показатели	Оценочные категории (k)

P(k/s)	0,11	0,25	0,54	0,73	0,95
P(k/n)	0,89	0,75	0,46	0,27	0,05

Определенные таким образом значения P(k/s) и P(k/n) имеют достаточно простой смысл в графической интерпретации – как площади под соответствующей функцией f(s) или f(n), взятые от одного значения s₀ до другого, и в аналитической – как интегралы этих функций на заданных соседними значениями s₀ отрезках s.

По сути дела такой подход означает, что мы пришли к теоретической модели, которая применялась в методе “Да – Нет” при использовании приемов получения нескольких значений λ₀ и s₀ в нескольких отдельных экспериментальных сериях (см. раздел 2.3.1). теперь эти несколько значений λ₀ и s₀ мы получаем в одном эксперименте за счет использования нескольких оценочных категорий. Вопрос заключается в том, как по полученным данным рассчитать пары значений P_обн и P_лт, необходимые для построения PX и оценки d¢.

Рассмотрим, как рассчитываются P_обн и P_лт в методе оценки, если в нем используется, например, пять оценочных категорий (как и в примере, приведенном выше). Определим необходимые для этого величины следующим образом:

P_s⁽^k) – вероятность отнесения сенсорного эффекта, вызванного стимулом, в k- ю категорию;

P_n⁽^k) –вероятность отнесения сенсорного эффекта, вызванного пустой пробой, в k -ю категорию.

Тогда значения P ⁽^k⁾ _обн и P ⁽^k⁾ _лт, рассчитываемые для соответствующих четырех значений λ₀ и s ₀⁽^k⁾, будут определяться способом, описанным в табл.11.

Таблица 11

Значение s₀⁽^k⁾	Оценочные категории, учитываемые при расчете P⁽^k⁾_обн и P⁽^k⁾_лт	Величины P⁽^k⁾_обн и P⁽^k⁾_лт, ожидаемые согласно теоретическому подходу в методе оценки
s₀⁽⁴⁾		P⁽⁴⁾_обн = P_s⁽⁵⁾ P⁽⁴⁾_лт = P_n⁽⁵⁾
s₀⁽³⁾	5+4	P⁽³⁾_обн = P_s⁽⁵⁾ + P_s⁽⁴⁾ P⁽³⁾_лт = P_n⁽⁵⁾ + P_n⁽⁴⁾
s₀⁽²⁾	5+4+3	P⁽²⁾_обн = P_s⁽⁵⁾ + P_s⁽⁴⁾ + P_s⁽³⁾ P⁽²⁾_лт = P_n⁽⁵⁾ + P_n⁽⁴⁾ + P_n⁽³⁾
s₀⁽¹⁾	5+4+3+2	P⁽¹⁾_обн = P_s⁽⁵⁾ + P_s⁽⁴⁾ + P_s⁽³⁾ + P_s⁽²⁾ P⁽¹⁾_лт = P_n⁽⁵⁾ + P_n⁽⁴⁾ + P_n⁽³⁾ + P_n⁽²⁾

Применим теперь подход, изложенный в таблице 11, к экспериментальным данным, содержащимся в таблице 9.

Поскольку число стимульных и пустых проб было равным - по 250, то, учитывая величины 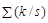и 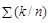из таблицы (9), получим:

P_s^(k) = 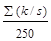, (25 a)

P_n^(k) = 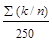. (25 b)

Рассчитанные по формулам (25 a, b) значения вероятности обнаружения и ложной тревоги для всех оценочных категорий приведены в табл.12.

После проведения вычислений получены 5 пар значений P_обн и P_лт, из которых четыре можно использовать для построения PX и расчета d¢. Значения P_обн и P_лт, полученные для 1-ой оценочной категории, в дальнейшем не рассматриваются, так как их величина по определению всегда должна быть равна 1.

Таблица 12

Значения вероятности обнаружения и ложной тревоги для всех s₀

Показатели	Оценочные категории

Вероятность отнесения стимула к данной оценочной категории P_s⁽^k)	0,05	0,10	0,20	0,30	0,35
Вероятность обнаружения стимула P⁽^k)_обн	1,00	0,95	0,85	0,65	0,35
Вероятность отнесения пустой пробы к данной оценочной категории P_n⁽^k)	0,39	0,31	0,17	0,11	0,02
Вероятность ложной тревоги P⁽^k)_лт	1,00	0,61	0,30	0,13	0,02

Для построения PX и расчета d¢ переведем нужные величины P⁽^k)_обн и P⁽^k⁾_лт в шкалу Z. Результаты пересчета даны в табл.13.

Таблица 13

Значения вероятности обнаружения и ложной тревоги для всех s₀

⇐ Предыдущая 14 15 16 17 181920 21 Следующая ⇒

Поделиться с друзьями:

Дата добавления: 2014-11-29; Просмотров: 448; Нарушение авторских прав?; Мы поможем в написании вашей работы!
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

studopedia.su - Студопедия (2013 - 2024) год. Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав! Последнее добавление

Генерация страницы за: 0.012 сек.