Образец оформления титульного листа

Задания для решения оптимизационной задачи методом наискорейшего спуска

Задания для решения оптимизационной задачи методом ломаных

Задания для выполнения курсовой работы

Алгоритм метода.

1. Проверить является ли целевая функция f(X) квадратичной

2. Задать погрешность вычислений

3. Найти градиент-вектор целевой функции:

4. Отыскать матрицу Q( где i=1..n, j= 1..n

5. Задать произвольным образом точку первоначального приближения Следующие точки приближения отыскиваются по формуле:

,

если поставлена задача на отыскание максимума целевой функции f(X).

если поставлена задача на отыскание минимума целевой функции f(X).

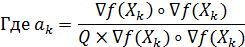
6. Условие оптимальности

Отыскать наименьшее значение целевой функции f(x) на интервале [a,b], используя метод, соответствующий варианту студента.

1. , [7;11], ε =0,01

2. 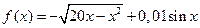, [9;11], ε =0,05

3. 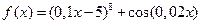, [49;51], ε =0,02

4. , [10;12], ε =0,01

5. , [0,8;1,2], ε =0,05

6. , [48;50], ε =0,02

7. 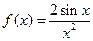, [8;12], ε =0,01

8. , [0,7;1,1], ε =0,05

9. 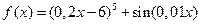, [48;50], ε =0,02

10. 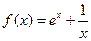, [0,1;2], ε =0,01

11. , [0;1], ε =0,01

12. , [10;12], ε =0,01

13.
14.
15.
16.
17.
18.
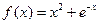
19.
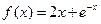
20.
21.
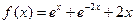
22.
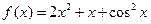
23.

Найти наименьшее (наибольшее) значение функции f(x) при ε = 0,001 заданным методом в соответствии с выданным вариантом.

1.

2.

3.

4.

5.

6.

7.

8.

9. а)

10. а)

11. 1. (min)

12. (min)

13. 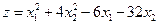(min)

14. 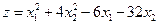(min)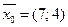

15. 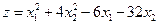(min)

16. 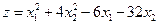(min)

17. (min)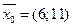

18. 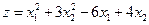(min)

19.

20.

21.

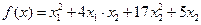
22.

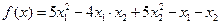
23.

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Ижевский государственный технический университет имени М.Т. Калашникова»

(ФГБОУ ВПО «ИжГТУ имени М.Т. Калашникова»)

Чайковский технологический институт (филиал )

Кафедра автомобильного транспорта

ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

к курсовой работе по дисциплине

«Методы оптимизации и вычислительной геометрии»

на тему:

«Разработка программного комплекса для решения оптимизационных задач»

Выполнил __________ (подпись) А. Ю. Ходырев

студент группы Э-11 о/з

Руководитель __________ (подпись) С.Ж. Козлова

доцент, к.п.н.

Чайковский 2014

Дата добавления: 2014-11-29