Метод обертання навколо вісі, перпендикулярної до однієї з площин проекцій

В цьому випадку всі точки геометричного образу рухаються в площинах рівня, які паралельні до однієї з площин проекції і перпендикулярні до інших. Тому одні точки будуть переміщуватися по дугам відповідних радіусів, а інші – по слідам площин, паралельних до вісі х.

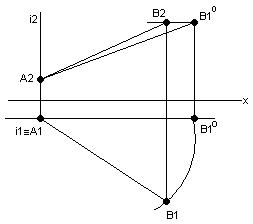
Приклад 1: Визначити натуральну величину АВ. (Рис. 8.3)

1. i є A

i┴ П1

2. A₁B₁-R₁

A₁B₁⁰║х

3. B₁⁰B₂⁰┴х

B₂⁰B₂║х

4. A₂B₂⁰ – HB

Рис. 8.3

Для рішення задачі необхідно знати центр та радіус обертання.

Приклад 2: визначити натуральну величину ∆АВС. (Рис. 8.4)

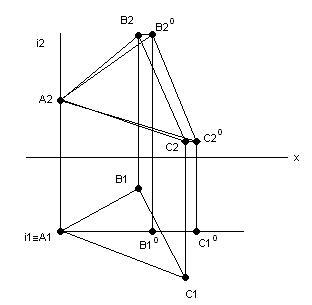
1. i є A

i┴ П1

2. В₂⁰, С₂⁰

А₂В₂⁰С₂⁰ – НВ

Рис. 8.4

3. Метод обертання навколо головних ліній креслення (фронталі і горизонталі)

Цей спосіб використовується. Якщо необхідно сумістити геометричний образ з площиною рівня.

В процесі переміщення кожна точка рухається у відповідних проекціюючих площинах.

Для рішення задачі необхідно визначити:

1) Центр обертання

2) Радіус обертання

Приклад 1: Побудувати нову проекцію точки А методом обертання навколо горизонталі. (Рис. 8.5).

1.∑п₁┴h₁

∑п₁ є A₁

∑п₁×h₁=O₁

O₂ є h₂

2. A₂1=A₁2

O₁2 – HB R

3. A₁^/ є ∑п₁

Рис. 8.5

Приклад 2: Методом обертання навколо горизонталі визначити натуральну величину ∆АВС (Рис.

1. ∑ є В

∑ ┴ h

∑п₁×h1=O₁

O₂ є h₂

2. O₁2 – R

B^/₁ є ∑п₁

3. Гп₁ є С₁

Гп₁┴ h₁

4. Гп₁×В₁^/1₁=С₁^/

5. А₁В₁^/С₁^/ - НВ

Рис. 8.6

Обертання навколо фронталі

Приклад 3: Побудувати нове положення т. А методом обертання навколо фронталі. (Рис. 8.7)

А,f

1.Гп₂┴f₂

Гп₂×f₂=O₂

O₁ є f₁

A₁1=A₂2

O₂2 – HB R

A₂^/ є Гп₂

Рис. 8.7

4. Метод обертання навколо слідів площини (суміщення)

Цей спосіб використовується, якщо необхідно виконати суміщення геометричного образу, який належить до заданої площини, з однією з площин проекцій.

Приклад 1: Методом обертання навколо горизонтального сліду площини побудувати нове положення проекції точки А. (Рис. 8.8)

1.∑х1₂ – R

1₂^/1₁┴∑п₁

2.∑х1₁^/ - ∑^/п₁

3.h₁^/║∑п₁

4.А₁^/А₁┴∑п₁

Рис. 8.8

Приклад 2. Визначити натуральну величину трикутника АВС. (Рис. 8.9)

Рис. 8.9

Контрольні питання.

1. Яку послідовність мають рішення задач методом площинно-паралельного переміщення (на прикладі прямої)

2. В чому полягає суть методу обертання навколо вісі перпендикулярної до однієї з площин проекцій?

3. Які основні елементи необхідно визначити при рішенні задач методом обертання навколо головних ліній креслення?

4. Наведіть приклад рішення задачі методом обертання навколо слідів площини.

Дата добавления: 2014-12-07