
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема множення зображень (теорема про згортку)
|
|
|
|
Теорема: Якщо оригінал 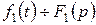 , а оригінал
, а оригінал 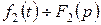 , то
, то
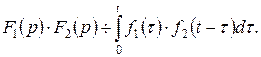 (6.7.1)
(6.7.1)
Доведення
Позначивши  , за визначенням зображення за Лапласом
, за визначенням зображення за Лапласом
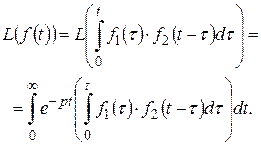 (6.7.2)
(6.7.2)
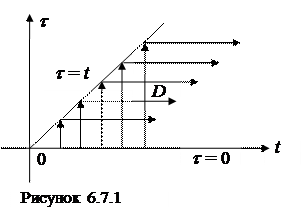
Інтеграл, що стоїть праворуч, є подвійний інтеграл, який береться по області 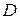 , обмеженій прямими
, обмеженій прямими 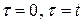 і при цьому:
і при цьому:

 |
Зміна порядку інтегрування в інтегралі праворуч у рівності (6.7.2) дає:
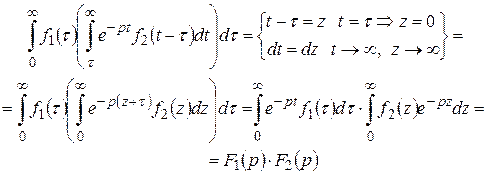 .
.
Отже
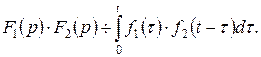
Інтеграл  називається згорткою функцій
називається згорткою функцій 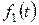 і
і 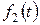 і позначається
і позначається  .
.
Отже оригінал, що відповідає добутку двох зображень, дорівнює згортці оригіналів співмножників.
Приклад 1. Застосовуючи теорему множення зображень, знайти оригінал, якщо,
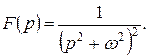
Розв¢язання
Маємо
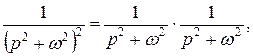
причому 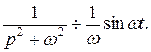
Тому, враховуючи, що

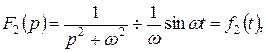
знаходимо:

тобто
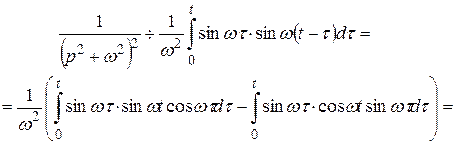
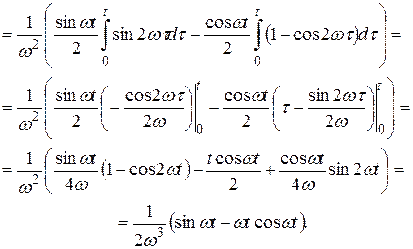
Відповідь:
 .
.
Приклад 2. (самостійно). Застосовуючи теорему про згортку, знайти оригінал, якщо 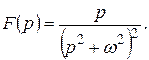
Відповідь:
6.8 Диференціювання оригіналів (зображення похідних оригіналів)
Зображення похідної 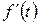 оригіналу
оригіналу 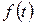 , якщо
, якщо 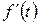 – оригінал, можна знайти за відомим зображенням
– оригінал, можна знайти за відомим зображенням 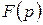 оригіналу
оригіналу 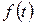 на підставі наступної теореми:
на підставі наступної теореми:
Теорема: Якщо, 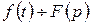 і
і 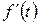 – оригінал, то
– оригінал, то 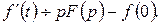
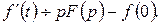 (6.8.1)
(6.8.1)
Доведення
На підставі означення зображення записується
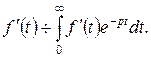
Шляхом інтегрування за частинами маємо:

тобто 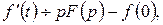 тому що в напівплощині
тому що в напівплощині 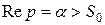 буде:
буде:
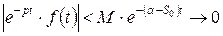 при
при  .
.
В окремому випадку, коли  , формула (6.8.1) має вигляд:
, формула (6.8.1) має вигляд:
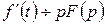 (6.8.2)
(6.8.2)
Таким чином, якщо початкове значення оригіналу дорівнює нулю, диференціювання оригіналу приводить до множення його зображення на параметр р. Застосувавши формулу (5.8.1) до другої похідної 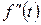 , одержуємо:
, одержуємо:
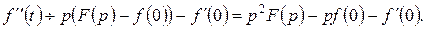
Аналогічно
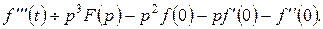 (6.8.3)
(6.8.3)
……………………………………………………
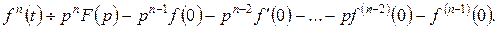
В окремому випадку, коли 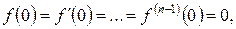 буде
буде
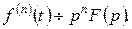 (6.8.4)
(6.8.4)
6.9 Інтегрування оригіналів(зображення інтегралів)
Теорема: Якщо 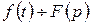 , то
, то 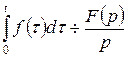 .
.
Доведення
Позначення  , а значить
, а значить 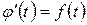 , приводить за теоремою єдності і теоремою диференціювання оригіналу до рівності:
, приводить за теоремою єдності і теоремою диференціювання оригіналу до рівності: 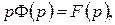 де
де 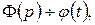 а
а  Таким чином,
Таким чином,  звідки маємо:
звідки маємо:
|
|
|
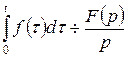 (6.9.1)
(6.9.1)
Приклад. Якщо 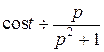 , то за теоремою інтегрування оригіналу
, то за теоремою інтегрування оригіналу
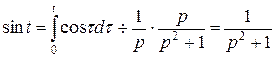 .
.
Відповідь:
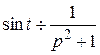 .
.
Зауваження. Формули диференціювання 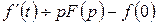 й інтегрування
й інтегрування 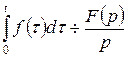 оригіналів, тобто формули (5.8.1) і (5.9.1), що визначають зображення похідної й інтеграла від оригіналу
оригіналів, тобто формули (5.8.1) і (5.9.1), що визначають зображення похідної й інтеграла від оригіналу 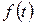 , відіграють найважливішу роль в операційному численні, бо з них випливає, що діям вищого аналізу – диференціюванню й інтегруванню функцій-оригіналів, відповідають алгебраїчні дії – множення і ділення відповідно їхніх зображень
, відіграють найважливішу роль в операційному численні, бо з них випливає, що діям вищого аналізу – диференціюванню й інтегруванню функцій-оригіналів, відповідають алгебраїчні дії – множення і ділення відповідно їхніх зображень 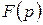 на параметр р. Отже, величину р можна формально розглядати як оператор диференціювання, а величину
на параметр р. Отже, величину р можна формально розглядати як оператор диференціювання, а величину 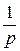 – як оператор інтегрування функції-оригіналу
– як оператор інтегрування функції-оригіналу 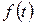 на відрізку
на відрізку 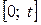 .
.
Слід також зазначити, що зображення значної кількості функцій-оригіналів, що зустрічаються на практиці, є дробово-раціональними алгебраїчними функціями параметра р.
Зазначене тут дає можливість багато задач вищого аналізу (розв¢язання диференціальних, інтегральних і інтегро-диференційних рівнянь і т.п.) звести до виконання алгебраїчних дій над зображеннями 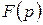 шуканих функцій-оригіналів
шуканих функцій-оригіналів 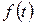 , які є розв¢язками таких задач.
, які є розв¢язками таких задач.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 3413; Нарушение авторских прав?; Мы поможем в написании вашей работы!