Числові вирази та їх види. Значення числового виразу та порядок обчислення значень числового виразу

1. У математиці під числовою алгеброю розуміють таку алгебру, основою множиною якої є числа і букви (під якими розуміють числа), основними операціями якої є додавання, віднімання, множення і ділення. З елементів основної множини за допомогою операцій утворюють інші елементи числової алгебри, а за допомогою основних операцій визначають інші нові операції, вводячи для них нові позначення.

Мова будь-якої алгебри складається з множини знаків, яку називають алфавітом цієї мови. Числова алгебра містить десять букв, які прийнято називати цифрами: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. За допомогою цифр згідно з певними правилами утворюються назви будь-яких чисел. Для позначення числових змінних використовують букви латинського алфавіту a, b, c, …, x, y, z або деякі з цих букв з індексами 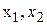... Інколи букви латинського алфавіту використовуються і для позначення числових сталих, тобто для позначення назв чисел. Для позначення певного конкретного, але не важливо якого числа, використовуються початкові букви латинського алфавіту a, b, c, …, а останніми буквами латинського алфавіту позначають змінні.

Для позначення операцій використовують відомі знаки „+”, „-”, „ 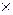”, „:”, а крім цього для запису чисел можуть використовувати праву „(” і ліву „)” дужки. Таким чином, алфавіт мови, на якій описується будь-яка числова алгебра, повинен включати таку множину: А={0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +. -, ´, ·,:, (,)}. Із елементів множини А утворюють скінченні послідовності цифр і букв, які називають виразами. Однак, так само як і в українській мові, не кожна послідовність цифр і букв алфавіту А утворює вираз. Наприклад, послідовність 5-) не є виразом. Саме тому постає питання про визначення поняття „вираз”. Хоча це поняття є одним з основних понять математики, зазначимо, що не існує загальноприйнятого означення поняття „вираз”. Саме тому наведемо індуктивне означення поняття „вираз”, в якому: 1) перераховуються елементарні вирази; 2) формулюються правила утворення нових виразів, із тих, що вже є; 3) стверджується, що інших виразів, крім тих, які можуть бути утворені у відповідності з першими двома пунктами визначення, не існує.

Означення: 1. Кожна окрема цифра або буква латинського алфавіту є виразом. Такі вирази називаються елементарними. 2. Якщо і вирази, то і – також вирази. 3. Інших виразів, крім тих, які можуть бути одержані у відповідності з пп. 1.2, не існує.

Для спрощення запису виразів прийняли такі домовленості:

а) опускати зовнішні дужки, які містять всередині себе всі решта букв, які складають вираз;

б) у виразі повинна бути однаковою кількість правих і лівих дужок;

в) вважати, що знак множення пов’язує сильніше, ніж знак додавання.

Наведене означення виразу та прийняті домовленості щодо правил запису виразів дозволяють відносно будь-якої послідовності цифр чи букв встановити чи є вона виразом, чи ні. Покажемо це на наступному прикладі.

Вправа: встановити чи є виразами такі послідовності букв: 1) (((3+b)●3))+(4●у)); 2) (((7+а)●3+(8●а)).

Розв’язання:

Перевіряємо, чи є у послідовностях зовнішні дужки, які містять всередині себе весь запис. Отже, у кожному з наведених записів слід опустити по одній зовнішній дужці. Оскільки у першому виразі є 4 лівих і 5 правих дужок, то такий запис не є виразом, бо не виконується друга домовленість. Аналогічно і другий запис не є виразом. Відповідно до третьої вимоги, слід опустити дужки, в яких стоїть лише дія множення. Таким чином, для того, щоб вказані записи були виразами, записи слід представити так: 1) (3+b)●3+4●у; 2) (7+а)●3+8●а.

У математиці існують різні класифікації виразів. Відповідно до однієї з них всі вирази поділяють на числові та нечислові. Щоб зрозуміти цю класифікацію приймемо наступне означення.

Дата добавления: 2014-12-07