Зачеты и экзамены

Лекции и практические занятия.

Во время экзаменационных сессий для студентов-заочников организуются лекции и практические занятия. Они носят по преимуществу обзорный характер. Их цель – обратить внимание на общую схему построения соответствующего раздела курса, подчеркнуть важнейшие факты, указать главные практические приложения, факты из истории науки.

Кроме того, на лекциях могут быть более подробно разобраны отдельные вопросы программы, отсутствующие или недостаточно полно освещенные в рекомендуемых пособиях.

На практических занятиях рассматриваются типовые задачи и примеры, а также дается образец решения какого-либо варианта контрольной работы с рекомендациями по ее выполнению и оформлению.

На экзаменах и зачетах выясняется, прежде всего, отчетливое усвоение всех теоретических и прикладных вопросов программы и умение применять полученные знания к решению практических задач. Определения, теоремы, правила должны формулироваться точно и с пониманием существа дела; решения задач в простейших случаях должны проделываться без ошибок и уверенно. Только при выполнении этих условий знания могут быть признаны удовлетворяющими требованиям, предъявляемым программой.

При подготовке к экзамену учебный материал рекомендуется повторять по учебнику и конспекту лекций.

Часть 3. ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ
КОНТРОЛЬНОЙ РАБОТЫ

При выполнении контрольных работ следует придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, могут быть не зачтены и возвращены студенту для переработки.

1) Каждую контрольную работу следует выполнять в отдельной тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.

2) На обложке тетради должны быть ясно написаны номер контрольной работы, название дисциплины, фамилия, имя, отчество студента, номер зачетной книжки, номер варианта, специальность и группа, в которой обучается студент. Здесь же указывается домашний адрес и дата отсылки работы в институт. В конце работы следует проставить дату ее выполнения и расписаться.

3) Номер варианта контрольной работы соответствует последней цифре номера зачетной книжки. Если номер зачетной книжки оканчивается цифрой «0», то студент выполняет 10-й вариант.

4) В работу включаются все задачи строго по положенному варианту. Работа, содержащая не все задачи варианта или не своего варианта, не зачитывается.

5) Решения задач надо располагать в порядке номеров, указанных в задании, сохраняя номера задач. Перед решением каждой задачи надо выписать полностью ее условие. Решения задач излагать подробно и аккуратно, объясняя все действия и делая необходимые чертежи.

6) Если работа не зачтена или сделаны замечания по решению задач, следует выполнить работу над ошибками в той же тетради. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для всех исправлений и дополнений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.

7) Студенты заочного отделения выполняют в течение 3 семестров пять контрольных работ. К экзамену в первом семестре допускаются студенты, у которых зачтены 1-я и 2-я контрольные работы. К зачету во втором семестре допускаются студенты, успешно сдавшие экзамен в первом семестре и имеющие зачтенные 3-ю и 4-ю контрольные работы. К экзамену в третьем семестре допускаются студенты, имеющие зачет за второй семестр и зачтенную 5-ю контрольную работу.

Часть 4. КОНТРОЛЬНЫЕ ЗАДАНИЯ

1.1. Контрольная работа № 1. «Аналитическая геометрия и векторная алгебра».

1. Даны вершины A (x ₁; y ₁), B (x ₂; y ₂), C (x ₃; y ₃) треугольника ABC. Найти: 1) длину стороны АВ; 2) уравнение медианы CM, проведенной из вершины С; 3) уравнение высоты СH, проведенной из вершины С; 4) уравнение прямой L, проходящей через вершину С параллельно стороне АВ; 5) длину высоты СH; 6) величину внутреннего угла А (в радианах). Сделать чертеж.

1. A (1; 1), B (7; 4), C (4; 5). 2. A (1; 1), B (–5; 4), C (–2; 5).

3. A (–1; 1), B (5; 4), C (2; 5). 4. A (–1; 1), B (–7; 4), C (–4; 5).

5. A (1; –1), B (7; 2), C (4; 5). 6. A (1; –1), B (–5; 2), C (–2; 3).

7. A (–1; –1), B (5; 2), C (2; 3). 8. A (–1; –1), B (–7; 2), C (–4; 3).

9. A (0; 1), B (6; 4), C (3; 5). 10. A (1; 0), B (7; 3), C (4; 4).

2. Составить уравнение и построить линию, для каждой точки которой выполняются следующее условие:

1) расстояние ее до точки F (–1; –2) равно расстоянию от прямой x = –3;

2) отношение расстояний до точки F (7; 0) и прямой x = 1 равно ;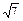

3) отношение расстояний до точки F (2; 0) и прямой x = 3 равно ;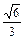

4) расстояние ее до точки F (3; 3) равно расстоянию от прямой x = –2;

5) отношение расстояний до точки F (2; 0) и прямой 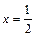равно ;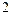

6) отношение расстояний до точки F (–1; 0) и прямой x = –9 равно ;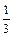

7) расстояние ее до точки F (–3; 2) равно расстоянию от прямой x = 2;

8) отношение расстояний до точки F (3; 0) и прямой x = 2 равно ;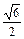

9) отношение расстояний до точки F (–4,5; 0) и прямой x = –8 равно ;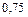

10) расстояние ее до точки F (1; 0) равно расстоянию от прямой x = 3.

3. Написать разложение вектора 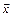по векторам , , .

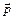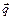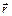1. , , , .

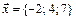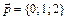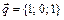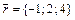2. , , , .

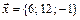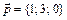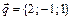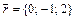3. , , , .

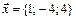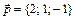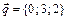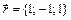4. , , , .

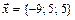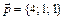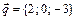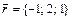5. , , , .

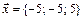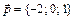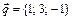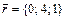6. , , , .

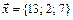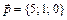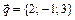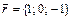7. , , , .

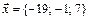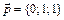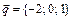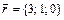8. , , , .

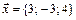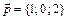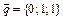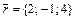9. , , , .

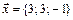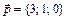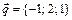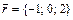10. , , , .

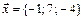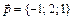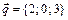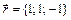4. Даны вершины A ₁(x ₁; y ₁; z ₁), A ₂(x ₂; y ₂; z ₂), A ₃(x ₃; y ₃; z ₃), A ₄(x ₄; y ₄; z ₄) пирамиды A ₁ A ₂ A ₃ A ₄. Найти: 1) угол между ребрами A ₁ A ₃ и A ₁ A ₄; 2) площадь грани A ₁ A ₂ A ₃; 3) уравнение плоскости, содержащей грань A ₁ A ₂ A ₃; 4) уравнение высоты пирамиды, проведенной через вершину A ₄. Сделать схематический чертеж.

1. A ₁(2; 1; –4), A ₂(1; –2; 3), A ₃(1; –2; –3), A ₄(5; –2; 1).

2. A ₁(2; –1; 3), A ₂(–5; 1; 1), A ₃(0; 3; –4), A ₄(–1; –3; 4).

3. A ₁(5; 3; 2), A ₂(1; –8; 8), A ₃(4; –1; 2), A ₄(1; 4; –1).

4. A ₁(–2; 3; 4), A ₂(4; 2; –1), A ₃(2; –1; 4), A ₄(–1; –1; 1).

5. A ₁(4; –4; 0), A ₂(–5; 3; 2), A ₃(8; 0; 1), A ₄(2; 2; 3).

6. A ₁(–3; –4; 0), A ₂(0; –1; 3), A ₃(–6; 4; 2), A ₄(–3; 0; 3).

7. A ₁(0; 4; –4), A ₂(5; 1; –1), A ₃(–1; –1; 3), A ₄(0; –3; 7).

8. A ₁(0; –6; 3), A ₂(3; 3; –3), A ₃(–3; –5; 2), A ₄(–1; –4; 0).

9. A ₁(2; –1; –3), A ₂(0; 0; 0), A ₃(5; –1; –1), A ₄(–1; –1; 1).

10. A ₁(1; 5; 8), A ₂(–2; 1; 4), A ₃(3; –2; –3), A ₄(1; –1; 0).

Дата добавления: 2014-11-29