
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Где – ковариация ценных бумаг i и j
|
|
|
|
В качестве целевой функции в данной задаче выступает минимум дисперсии

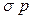 2 =
2 = 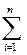

 Wi * Wj, min
Wi * Wj, min
В качестве ограничения выступаетсредняя доходность портфеля
Rр =  RiWi,
RiWi,
где Ri, Wi– доходность и удельный вес включенной в портфель i – ой ценной бумаги.
При этом сумма удельных весов бумаг должна быть равна 1, т.е.
 Wi. = 1.
Wi. = 1.
Для того, чтобы найти решение такой задачи вводят набор переменных λ1 и λ2, называемых множителями Лагранжа и составляется функция Лагранжа:
L = 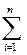

 Wi * Wj +λ1 *(
Wi * Wj +λ1 *(  RiWi - Rр)+ λ2 *(
RiWi - Rр)+ λ2 *(  Wi. - 1),
Wi. - 1),
где λ1, λ2— множители Лагранжа.
Структура портфеля, имеющего минимизирующий риск, определяется решением системы уравнений:
dL/dWi =0
dL/d λк, =0.
где к = 1,2.
Данная система уравнений представляет собой модель, позволяющая определить структуру оптимального портфеля.
Пример. Необходимо сформировать портфель из двух ценных бумаг Альфа и Омега, обладающий минимальным риском. Бумаги имеют следующие показатели доходности и риска: RА = 12%, RО = 5.1%,  = 21.1%,
= 21.1%,  = 8.3%., коэффициент корреляции равен 0.18. Доходность портфеля Rр должна составлять 8.9%. Функция Лагранжа для данной задачи будет иметь вид
= 8.3%., коэффициент корреляции равен 0.18. Доходность портфеля Rр должна составлять 8.9%. Функция Лагранжа для данной задачи будет иметь вид
L =  *WА2 +
*WА2 + 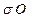 **WО2 +2*WА * WО*
**WО2 +2*WА * WО* 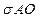 + λ1 *(RАWА + RОWО – Rр)+ λ2 *(WА+. WО – 1).
+ λ1 *(RАWА + RОWО – Rр)+ λ2 *(WА+. WО – 1).
dL/dWА = 2  *WА +2* WО*
*WА +2* WО* 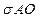 + λ1 * RА + λ2 = 0
+ λ1 * RА + λ2 = 0
dL/dW2 = 2 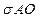 *WА +2* WО*
*WА +2* WО* 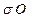 + λ1 * RО + λ2 = 0
+ λ1 * RО + λ2 = 0
dL/d λ1, = RАWА + RОWО – Rр = 0.
dL/d λ2, = WА+. WО - 1 =0
Представим данную систему уравнений в матричном виде:
2 
| 2 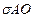
| RА | WА | ||||
2 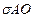
| 2 
| RО | * | WО | = | ||
| RА | RО | λ1 | Rр | ||||
| Λ2 |
2 
| 2 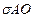
| RА | WА | ||||
2 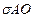
| 2 
| RО | * | WО | = | ||
| RА | RО | λ1 | Rр | ||||
| Λ2 |
Если обозначить матрицу через Н, вектор – через А и вектор в правой части – через G, то получим уравнения в матричной форме:
Н*А = G,
А = Н-1* G.
Рассмотрим далее задачу для случая портфеля состоящего из трех ценных бумаг:
L =  *W12 +
*W12 +  *W22 +
*W22 +  *W32 +2*W1 * W2*
*W32 +2*W1 * W2*  +2*W1 * W3*
+2*W1 * W3*  +2*W2 * W3*
+2*W2 * W3*  + λ1 *(R1W1 + R2W2 + R3W3 – Rр)+ λ2 *(W1+. W2 W3 – 1).
+ λ1 *(R1W1 + R2W2 + R3W3 – Rр)+ λ2 *(W1+. W2 W3 – 1).
dL/dW1 = 2  *W1 +2* W2*
*W1 +2* W2*  + 2W3*
+ 2W3*  + λ1 * R1 + λ2 = 0
+ λ1 * R1 + λ2 = 0
dL/dW2 = 2  *W1 +2* W2*
*W1 +2* W2*  + 2W3*
+ 2W3*  + λ1 * R2 + λ2 = 0
+ λ1 * R2 + λ2 = 0
dL/dW3 = 2  *W1 +2* W2*
*W1 +2* W2*  + 2W3*
+ 2W3*  + λ1 * R3 + λ2
+ λ1 * R3 + λ2
dL/d λ1, = R1W1 + R2W2 + R3W3 – Rр = 0.
dL/d λ2, = W1+. W2 W3 - 1.
Представим данную систему уравнений в матричном виде:
2 
| 2 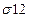
| 2 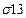
| R1 | W1 | ||||
2 
| 2 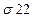
| 2 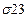
| R2 | W2 | ||||
2 
| 2 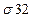
| 2 
| R3 | * | W3 | = | ||
| R1 | R2 | R3 | λ1 | Rр | ||||
| Λ2 |
Если обозначить матрицу через Н, вектор – через А и вектор в правой части – через G, то получим уравнения в матричной форме:
Н*А = G,
А = Н-1* G.
Пример. Имеются три акции. Их параметры представлены в таблице
| Номер акции | Ri | 
| 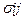
|
| 0,06 0,09 0,18 | 0,35 0,42 0,75 |  = -0,1 = -0,1
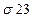 = 0,42 = 0,42
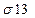 = 0,30 = 0,30
|
Матрица Н G и Н-1 для данной задачи будет иметь следующий вид
| 0,7 | -0,2 | 0,6 | 0,06 | |
| -0,2 | 0,84 | 1,0 | 0,09 | |
| 0,6 | 1,0 | 1,5 | 0,18 | |
| 0,06 | 0,09 | 0,18 | ||
| Rр |
| 0,416 | -0,555 | 0,138 | -3,481 | 0,723 |
| -0,55 | 0,74 | -0,185 | -6,47 | 1,035 |
| 0,139 | -0,185 | 0,046 | 9,951 | -0,759 |
| -3,481 | -6,4695 | 9,951 | -12,836 | -4,057 |
| 0,724 | 1,035 | -0,759 | -4,057 | -0,399 |
Удельные веса акций будут равны
| W1 | - 3,481* Rр +0,723 | |
| W2 | = | -6,470* Rр +1,035 |
| W3 | 9,951* Rр +0,759 |
Если инвестор хочет получить доходность Rр = 12%, то получим: W1 = 0,305, W2 = 0,259, W3 = 0,435.
Рассмотренный пример иллюстрирует вычислительные трудности, связанные с использованием модели Марковица. Так сам Марковиц подсчитал, что анализ 100 ценных бумаг требует вычисления 100 ожидаемых значений доходности, 100 дисперсий и почти 5000 ковариаций. В связи с этим уже 1962 корпорацией IBM была разработана первая компьютерная программа для реализации модели Марковица.
|
|
|
|
|
Дата добавления: 2014-12-07; Просмотров: 450; Нарушение авторских прав?; Мы поможем в написании вашей работы!