Основные свойства и характеристики информации

Для того чтобы иметь возможность использовать понятие информации при решении различных инже­нерно-психологических задач, нужно знать основные характеристики и свойства информации. Основными ее характеристиками являются количество, ценность, избыточность и достоверность. Количество информа­ции является важнейшей характеристикой информа­ции, используемой в инженерной психологии. Простой формальный аппарат для оценки количества информа­ции, содержащейся в сообщении, разработан в клас­сической теории информации (статистической теории связи).

При таком подходе количество информации опре­деляется величиной уменьшения энтропии (неопреде­ленности ситуации) после получения человеком каких-либо сведений. Величина энтропии рассчитывается по формуле

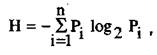(2.2)

где P_i — вероятность i-того сигнала (нахождения сис­темы в i-том состоянии);

п — общее число различных сигналов (состояний системы).

В случае, если все сигналы равновероятны (P_i 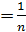), то энтропия при данном n достигает своего максималь­ного значения, равного

H = log₂ n, (2.3)

При поступлении сообщения о каком-либо собы­тии энтропия системы уменьшается, причем это умень­шение и характеризует количество поступившей ин­формации

I = Н—Н₀, (2.4)

где Н и Н₀ — соответственно априорная (доопытная) и апостериорная (послеопытная, т. е. после получения сообщения) энтропия.

В том практически важном случае, когда после по­ступления сведений состояние системы стало полнос­тью определенным (а именно такой случай наиболее характерен для деятельности оператора), то количество информации численно равно априорной энтропии си­стемы, т. е. I = Н.

В формулах (2.2) и (2.3) логарифм может браться по любому основанию, но наиболее часто использу­ется основание, равное двум. При этом единица из­мерения количества информации носит название двоичной единицы информации (деи), или бита. Ин­формация в один бит будет иметь место в том случае, когда осуществляется выбор одного из двух равнове­роятных событий. Передача информации, равной од­ному биту позволяет уменьшить неопределенность ситуации вдвое.

Количество информации, перерабатываемое опе­ратором в единицу времени, называется скоростью переработки информации оператором, то есть V_ОП 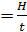. Наибольшая скорость переработки информации чело­веком, рассматриваемом в качестве канала связи, т. е. канала передачи информации со средств ее отображе­ния к органам управления, называется пропускной способностью оператора. Ее величина в общем случае определяется формулой

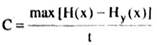(2.5)

где Н(х) — энтропия источника сообщений; Н_у(х) — ус­ловная энтропия, характеризующая влияние шумов (помех) на передачу сообщений, она характеризует по­тери информации в процессе ее передачи; t — время передачи информации.

Любой канал связи, в том числе и систему перера­ботки и передачи информации оператором, можно представить в виде нескольких последовательных уча­стков передачи информации. Очевидно, пропускная способность канала в целом будет определяться про­пускной способностью того участка, для которого она минимальна. Подробнее этот вопрос рассматривается при изучении информационных характеристик зри­тельного анализатора.

Количество информации характеризует объем по­лученных человеком сведений, оно совершенно не зависит от свойств получателя сообщений и характе­ризует только одну сторону информации — структур­ную, статистическую. Однако кроме нее есть и праг­матическая сторона, которая всегда связана с целью деятельности человека и поэтому зависит от его инди­видуальных качеств. Эта сторона информации харак­теризуется таким понятием как ценность информации. Знание ценности информации позволяет рационально размещать датчики и измерительные приборы на ра­бочем месте оператора, сокращать общий объем инфор­мационного потока, разумно планировать очередность передачи сообщений оператору, назначая приоритеты согласно ценности, и т. п.

Ценность информации характеризует значение ин­формации для получателя. Для ее количественной оцен­ки разработано три основных подхода [цит. по 46, 77].

1. Ценность информации определяется по тому, на­сколько получаемое сообщение способствует дос­тижению цели. Количественно показатель ценно­сти определяется формулой

(2.6)

где Р₀ и P₁ и — соответственно вероятность достиже­ния цели до и после получения сообщения.

При таком подходе ценность информации, также как и ее количество, выражается в двоичных единицах (А.А.Харкевич).

2. Понятие ценности информации выводится из свя­зи теории информации с теорией оптимального уп­равления. Для этого рассматривается система слу­чайных величин х и система их оценки у. Средняя степень неопределенности существующих оценок определяется функцией штрафов f(x, у). Ценность же полученной информации находится по тому, на­сколько эта информация минимизирует функцию штрафов, т. е. делает оценки более определенными (Р.Л. Стратонович).

3. Ценность информации определяется исходя из того, насколько она снижает степень неопределен­ности (трудности) решаемой задачи. Если задача с п равновероятными исходами имеет начальную неопределенность H_Q = log₂ n, а после поступле­ния сообщения q относительно вероятности отве­тов Р ее неопределенность стала, то цен­ность информации равна H= ,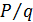

(2.7)

При таком подходе ценность информации опреде­ляется уже не по ее влиянию на статистическую нео­пределенность отдельных сообщений, а по тому, в ка­кой мере она снимает неопределенность самого метода решения. Здесь может учитываться и ложная информа­ция, повышающая неопределенность задачи (М.М. Бонград).

Рассмотренные методы определяют ценность ин­формации для человека исходя из ее значения для него. Осознание ценности информации человеком будет вызывать у него соответствующие эмоции. Поэтому приведенные показатели могут служить также косвен­ными мерами уровня эмоциональной реакции челове­ка на информацию.

Как уже отмечалось, наличие ложной информации снижает ее общую ценность. Поэтому важной харак­теристикой информации является ее достоверность» Под достоверностью информации понимается безоши­бочная (не искаженная) передача, переработка и хра­нение информации в системе при заданных условиях ее эксплуатации [214]. Качественно достоверность информации определяется как ее свойство на выходе системы соответствовать информации, поступившей на ее вход. Количественно достоверность информации оценивается такими показателями, как наработка на информационную ошибку, интенсивность информаци­онных ошибок, вероятность безошибочности информа­ции.

При расчетах этих показателях принимаются сле­дующие допущения:

■ информационные ошибки (искажения) в составных ком­понентах системы — события независимые, случайные;

■ поток информационных ошибок является простейшим;

■ появление информационный ошибки (искажения) в от­дельной компоненте системы приводит к появлению ошибки на выходе системы;

■ критерии появления (наличия) ошибок точно определены и их можно использовать для диагностики ошибок.

С учетом этих допущений в работе [214] предло­жены формулы для определения показателей достовер­ности информации. Наработка на информационную ошибку рассчитывается по формуле

(2.8)

где N_∑ — суммарная информационная наработка систе­мы в единицах обрабатываемой информации, элемен­тах (суммарная информационная нагрузка системы);

N_ош — число возникших ошибок в системе (искаженных элементов информации) в рассматриваемой суммарной информационной нагрузке.

В некоторых случаях рассматривают также вре­менную наработку системы (с определенным быстро­действием) на информационную ошибку

где t_∑и n(t_∑) — соответственно суммарное время нара­ботки и возникшее за это время число информацион­ных ошибок.

Под интенсивностью ошибок (искажений) пони­мается отношение числа ошибок n_ош (t), возникших за некоторый интервал времени t, к произведению информационной нагрузки за этот же интервал на его длительность, то есть

(2.9)

Вероятностью безошибочности (не искаженности) информации называется вероятность того, что в опре­деленных условиях работы в пределах заданной инфор­мационной нагрузки (заданной продолжительности) ошибка (искажение) в информации не появится. Эта вероятность по статистическим данным находится по формуле

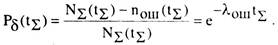(2.10)

Основным методом повышения достоверности информации в информационных системах (как техни­ческих, так и в системе переработки информации че­ловеком) является применение помехоустойчивых ко­дов [14, 91]. Применение помехоустойчивых кодов связано с введением избыточности в исходную инфор­мацию.

Избыточность информации есть некоторая вели­чина r, которой измеряется относительная доля излиш­не используемых сообщений в некотором алфавите. Она определяется формулой

(2.11)

где Н — энтропщия сообщения, п — средняя длина кодового слова, М — число символов алфавита.

Естественным языкам свойственна значительная избыточность информации (например, для русского языка r = 0,5...0,8). Избыточность информации может быть естественной (например, естественные языки, изображения и т. п.) и искусственной. Последняя спе­циально вводится для улучшения помехоустойчивости, достоверности и надежности передачи и хранения информации [166]. В общем случае избыточность ин­формации оказывает двоякое влияние на характеристики информационных систем, в том числе и на про­цессы переработки информации человеком.

С одной стороны, избыточность информации су­щественно повышает ее помехоустойчивость, дает воз­можность восстановить искаженную информацию. На­пример, искажение или потеря отдельных букв, слов, а иногда и фраз позволяет правильно распознать смысл письменного или устного сообщения; искажение одно­го, двух сегментов знакосинтезирующих цифровых индикаторов позволяет в ряде случаев восстановить истинное значение отображаемой цифры и т. д. При­мером избыточности в информационных структурах мозга является парность некоторых анализаторов (зри­тельного, слухового), что повышает надежность их работы. Избыточную информацию не следует путать с иррелевантной, которая является помехой и мешает нормальной работе оператора. Существует три основ­ных способа введения избыточности: многократное повторение одной и той же информации; введение в сигналы дополнительных элементов; метод избыточных переменных.

С другой стороны, избыточность усложняет систе­му, увеличивает время обработки информации, снижа­ет реальную пропускную способность каналов связи. Поэтому определение необходимой избыточности ре­шается в каждом конкретном случае исходя из особен­ностей решаемой задачи и возможных ограничений. В случае необходимости для уменьшения избыточнос­ти применяют методы, разработанные в теории опти­мального кодирования, а также специальные методы сжатия информации.

Сжатием информации (сжатием данных) называ­ется представление информации (данных) меньшим числом битов по сравнению с первоначальным. Разли­чают сжатие информации без потери информации и с потерей некоторой ее части, несущественной для ре­шаемых задач. К первой группе относятся методы ко­дирования, использующие статистику потока сигналов для получения выигрыша в среднем, например, коди­рование короткими комбинациями символов более часто встречающихся элементов сообщения (код Мор­зе), Ко второй группе относятся методы, основанные на различных аппроксимациях данных, например, кодирование непрерывной кривой дискретными отсче­тами, основанное на теории Шеннона — Котельникова.

По способу устранения избыточности все методы сжатия информации делятся на три группы: 1) струк­турные, предусматривающие дискретное строение массивов информации и предполагающее их простей­шее кодирование; 2) статистические, определяемые понятием энтропии как меры неопределенности, учи­тывающий вероятности появления, а следовательно, и информативности тех или иных сообщений (см. выше); 3) семантические, учитывающие целесообраз­ность, ценность, полезность или существенность ин­формации.

При инженерно-психологическом проектировании для уменьшения времени и вероятности ошибочных действий оператора при вводе и считывании инфор­мации сжатие является основным методом создания компактных систем ввода и систем отображения ин­формации, поскольку возможности их пространствен­ного уплотнения ограничены психофизиологическими особенностями оператора. Для этого используется все рассмотренные методы исключения избыточности, обеспечивающие минимизацию числа кнопок их раз­мещение на панели управления с учетом структуры системы управления, числа команд и частоты обраще­ния к кнопкам пульта. Аналогичное делается для со­здания компактных систем отображения информации вызывного типа с учетом возможного числа сигналов, вероятности их поступления, а также важности и сроч­ности их обработки.

Информация, циркулирующая в системе «чело­век—машина» может обладать такими нежелательны­ми свойствами, как старение и рассеяние, что в случае их неучета приводит к снижению эффективности про­цесса управления.

Старение информации связано с конечным време­нем ее передачи и обработки. Наиболее часто задерж­ки на пути информации от источника до получателя происходят в различного рода накопителях (запомина­ющих устройствах) и каналах связи. Нередко задерж­ку вводят искусственно с целью получить взамен мень­шую вероятность ошибки. Примером является многократное повторение одной и той же информации (временная избыточность). Однако чаще всего старе­ние информации возникает естественным путем.

Если информация носит оперативный характер и используется для принятия решений или выработки управляющих воздействий, то за время задержки она стареет. В результате управление либо принятое реше­ние могут оказаться не эффективным. Для устранения этого оператор должен экстраполировать полученную информацию на некоторое время вперед, то есть осу­ществлять прогнозирование изменения информации во времени. От точности прогноза и будет зависеть эф­фективность управления.

К настоящему времени разработаны следующие алгоритмы прогноза: прогноз по последнему значению, прогноз по математическому ожиданию, статистичес­кий прогноз по одной точке. Каждый из них имеет свои преимущества и недостатки [46], само прогнозирование может осуществляться либо автоматически (тогда в систему обработки и передачи информации допол­нительно вводится специальное устройство — экстраполятор), либо оператором. В этом случае он должен быть специально обучен навыкам экстраполяции. Осо­бое значение при этом имеет способность оператора к антиципации (от лат. anticipatio — предвосхищаю), т. е. способности предвидеть будущие, предстоящие собы­тия. Поскольку изменение ситуации за время прогно­за зачастую представляет собой случайный процесс, то оператор должен уметь осуществлять вероятност­ное прогнозирование. Все это позволит ему более ра­ционально (разумеется, в определенных пределах) ис­пользовать стареющую информацию.

Зная количественные оценки стареющей информа­ции, можно вовремя очищать запоминающие устройства от устаревших данных, назначать сроки принятия ре­шений так, чтобы они базировались на достоверных, не устаревших сведениях, назначать из тех же соображе­ний допустимое время передачи информации и т. п. [46].

В практике экспериментирования и контроля хода технологических процессов обычной является ситуа­ция, когда о значениях какого-либо параметра судят по результатам других величин, связанных с ним. Такой метод называется косвенными измерениями. При этом информация может оказаться рассеянной среди данных о других величинах. Помимо этого часто возника­ет ситуация, когда оператору для решения текущей задачи приходится использовать информацию, посту­пающую от различных, отстоящих друг от друга источ­ников. Рассмотренные ситуации роднит то обстоятель­ство, что в них имеет место рассеяние информации.

Различают два основных вида рассеяния. Во-пер­вых, рассеяние по ансамблю источников, когда нуж­ная для решения задачи информация находится в раз­ных местах информационного поля. Во-вторых, — это рассеяние по времени, когда информацию о каком-либо факте несут не только текущие события либо значения наблюдаемых процессов, но и отстоящие от них на некоторое время. В этом случае для решения задачи одновременно нужно использовать сведения, относящиеся к различным моментам времени.

Следовательно, в общем случае нужная для реше­ния задачи информация может оказаться рассеянной как среди других источников, так и относится к раз­ным временным интервалам. Оказывается, что специ­альная обработка позволяет собрать такие данные, сконцентрировать их. Перспективными путями кон­центрации рассеянной информации являются, с одной стороны, запоминающие устройства действующие на ассоциативном принципе, а с другой — диалоговые системы общения человека с ЭВМ, обеспечивающие итеративное повышение уровня взаимопонимания [46]. Концентрации информации способствует также при­менение компактных устройств ввода и отображения информации, рациональная компоновка рабочего мес­та оператора, упорядоченное размещение элементов и их логическая группировка, своевременная подсказка оператору о необходимых действиях и т. п.

Дата добавления: 2014-12-07